Bài 37 trang 142 SBT toán 8 tập 2
Giải bài 37 trang 142 sách bài tập toán 8. Đáy của lăng trụ đứng là một hình thang cân có các cạnh b = 11mm, a = 15mm và chiều cao hT = 7mm (h.127) ...
Đề bài
Đáy của lăng trụ đứng là một hình thang cân có các cạnh \(b = 11mm, a = 15mm\) và chiều cao \(h_T= 7mm\) (h.127)
Chiều cao của hình lăng trụ là \(h = 14mm.\) Tính diện tích xung quanh của lăng trụ.
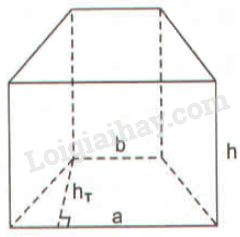
Phương pháp giải - Xem chi tiết
Sử dụng: Diện tích xung quanh của hình lăng trụ đứng bằng tổng diện tích các mặt bên hoặc bằng chu vi đáy nhân với chiều cao.
\({S_{xq}} = 2p.h\)
Trong đó: \(p\) là nửa chu vi đáy, \(h\) là chiều cao
Lời giải chi tiết
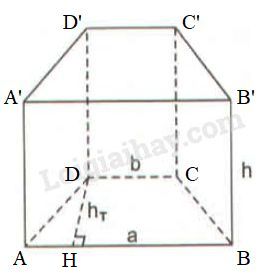
Giả sử hình lăng trụ có \(CD = 11mm\); \(AB = 15mm;\) \(DH = 7mm\) và \(BB'=14mm\).
Ta có: \(\displaystyle AH = {{AB - CD} \over 2} = {{15 - 11} \over 2} \)\(\,= 2\;(mm)\) (vì \(ABCD\) là hình thang cân).
Áp dụng định lí Py-ta-go vào tam giác vuông \(AHD\), ta có:
\( A{D^2} = A{H^2} + H{D^2} = {2^2} + {7^2} = 53 \)
\( \Rightarrow AD = \sqrt {53}\; (mm)\)
Vì \(ABCD\) là hình thang cân nên \(BC = AD= \sqrt {53}\; (mm)\)
Ta có:
\( {S_{xq}} = \left( {AB + BC + DC + AD} \right).BB' \)
\(= \left( {AB + DC + 2AD} \right).BB' \)
\(= \left( {15 + 11 + 2\sqrt {53} } \right).14 \)
\(= \left( {364 + 28\sqrt {53} } \right)(m{m^2}) \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 37 trang 142 SBT toán 8 tập 2 timdapan.com"







