Bài 37 trang 139 Vở bài tập toán 8 tập 2
Giải bài 37 trang 139 VBT toán 8 tập 2. Tính thể tích của hình chóp đều...
Đề bài
a) Tính thể tích của hình chóp đều (h.136).
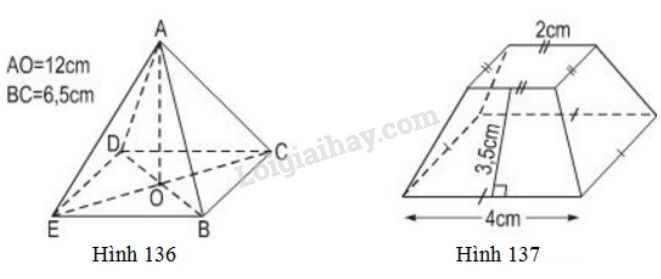
b) Tính diện tích xung quanh của hình chóp cụt đều (h.137).
(Hướng dẫn: Diện tích cần tính bằng tổng diện tích các mặt xung quanh. Các mặt xung quanh là những hình thang cân với cùng chiều cao, các cạnh đáy tương ứng bằng nhau, các cạnh bên bằng nhau)
Phương pháp giải - Xem chi tiết
- Tính thể tích hình chóp theo công thức: \(V = \dfrac{1}{3} .S.h\), trong đó \(S\) là diện tích đáy, \(h\) là chiều cao.
- Tính diện tích hình thang theo công thức: \(S = \dfrac{(a+b). h}{2} \), trong đó \(a,\; b\) là là hai đáy của hình thang, \(h\) là chiều cao.
Lời giải chi tiết
a) Diện tích đáy của hình chóp đều:
\( S = BC^2 = 6,5^2 = 42,25 (cm^2)\)
Thể tích hình chóp đều là:
\( V = \dfrac{1}{3} .S.h = \dfrac{1}{3} . 42,25 .12 = 169\)\(\, (cm^3)\)
b) Các mặt xung quanh là những hình thang cân đáy nhỏ \(2cm\), đáy lớn \(4cm\) , chiều cao \(3,5cm\).
Diện tích xung quanh của hình chóp cụt đều là:
\(S_{xq} = 4. \dfrac{(2+4). 3,5}{2} =42 (cm^2) \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 37 trang 139 Vở bài tập toán 8 tập 2 timdapan.com"







