Bài 34 - 35.9,34 - 35.10 trang 86 SBT Vật lí 10

34 - 35.9.

Một chiếc cột bê tông cốt thép chịu lực nén F thẳng đứng do tải trọng đè lên nó. Giả sử suất đàn hồi của bê tông bằng 1/10 của thép, còn diện tích tiết diện  ngang của thép bằng khoảng 1/20 của bê tông. Hãy tính phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột này.

Phương pháp giải:

Áp dụng công thức tính ứng suất \(\sigma  = \dfrac{F}{S} = E\dfrac{{\left| {\Delta \ell } \right|}}{{{\ell _0}}}\)

Lời giải chi tiết:

Gọi F₁ là phần lực nén do tải trọng tác dụng lên phần bê tông của chiếc cột và F₂ là phần lực nén do tải trọng tác dụng lên phần cốt thép của chiếc cột. Áp dụng định luật Húc, ta có :

\({F_1} = {E_1}{{{S_1}} \over l}\Delta l\) và \({F_2} = {E_2}{{{S_2}} \over l}\Delta l\)

So sánh F₁ với F₂ , với chú ý E₁/E₂ = 1/10 và S₂/S₁ = 1/20, ta tìm được

\({{{F_1}} \over {{F_2}}} = {{{E_1}{S_1}} \over {{E_2}{S_2}}} = 2\)

Vì F₁ + F₂ = F, nên ta suy ra : F₁ = 2/3 F

Như vậy, lực nén lên bê tông bằng 2/3 lực nén của tải trọng tác dụng lên cột.

34 - 35.10.

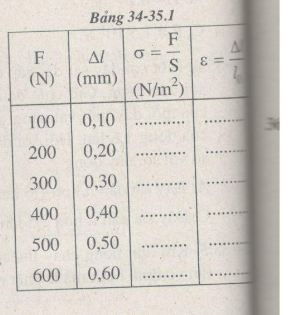
Người ta dùng một thanh sắt tròn có độ dài ban đầu l₀= 50 cm và tiết diện ngang S = 2,5 mm². Kéo dãn thanh sắt bằng lực F có cường độ tăng dần và đo độ dãn dài Δl tương ứng của nó (Bảng 34-35. 1).

a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên nó trong mỗi lần đo (Bảng 34-35. 1).

b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào ε.

c) Dựa vào đồ thị vẽ được, tìm giá trị của suất đàn hồi E và hệ số đàn hồi k.

Phương pháp giải:

Áp dụng công thức tính ứng suất \(\sigma  = \dfrac{F}{S} = E\dfrac{{\left| {\Delta \ell } \right|}}{{{\ell _0}}}\)

Lời giải chi tiết:

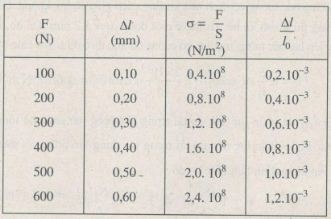
a) Tính độ dãn dài tỉ đối ε của thanh sắt và ứng suất σ của lực kéo tác dụng lên thanh sắt trong mỗi lần đo.

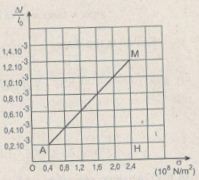
b) Vẽ đồ thị biểu diễn sự phụ thuộc của ε vào σ.

Chọn tỉ lệ vẽ trên các trục tọa độ:

- Trục hoành: 1 cm → σ = 0,5.10⁸ N/m².

- Trục tung: 1 cm → ε = 0,2.10^-3.

Đồ thị có dạng đường thẳng chứng tỏ độ biến dạng tỉ đối Δl/l₀ của thanh sắt tỉ lệ thuận với ứng suất σ của lực kéo tác dụng lên thanh sắt, nghĩa là:

\(\varepsilon = {{\Delta l} \over {{l_0}}} = a\varepsilon \)

Hệ số tỉ lệ a được xác định bởi hệ số góc của đường biểu diễn đồ thị:

\(\tan \theta = {{MH} \over {AH}} = {{1,{{2.10}^{ - 3}} - 0,{{2.10}^{ - 3}}} \over {2,{{4.10}^8} - 0,{{4.10}^8}}} = 0,{5.10^{ - 11}}\)

c) Tìm giá trị của suất đàn hồi E và hệ số đàn hồi k của thanh sắt.

Theo định luật Húc :\(F = k\left| {\Delta l} \right| = E{S \over {{l_0}}}\Delta l\) , ta suy ra  \({{\Delta l} \over {{l_0}}} = {1 \over E}.{F \over S}\)

Từ đó tìm đươc suất đàn hồi :  \(E = {1 \over {\tan \theta }} = {1 \over {0,{{5.10}^{ - 11}}}} = {20.10^{10}}Pa\)

và hệ số đàn hồi:   \(k = E{S \over {{l_0}}} = {20.10^{10}}.{{2,{{5.10}^{ - 6}}} \over {{{50.10}^{ - 2}}}} = {1.10^6}N/m\)