Giải bài 3.25 trang 44 sách bài tập toán 7 - Kết nối tri thức với cuộc sống
Cho hình 3.25
Đề bài
Cho hình 3.25
a) Giải thích tại sao \(Ax\parallel By\).
b) Tính số đo góc ACB.
Phương pháp giải - Xem chi tiết
a)
Chỉ ra Ax và By cùng vuông góc với đường thẳng thứ 3.
b)
Kẻ \(Ct\parallel Ax\)
-Tính góc Act
-Tính góc BCt.
Lời giải chi tiết
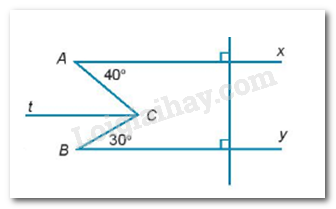
a)
Ta có: \(\left\{ \begin{array}{l}Ax \bot c\\By \bot c\end{array} \right. \Rightarrow Ax\parallel By\).
b)
Vẽ tia \(Ct\parallel Ax\).
Ta có: \(Ct\parallel Ax\)mà \(Ax\parallel By\) nên \(Ct\parallel By\) (Tính chất ba đường thẳng song song).
\(Ax\parallel Ct \Rightarrow \widehat {ACt} = \widehat {CAx} = {40^0}\) (hai góc so le trong)
\(Ct\parallel By \Rightarrow \widehat {tCB} = \widehat {CBy} = {30^0}\) (hai góc so le trong)
Tia Ct nằm giữa hai tia CA và CB nên:
\(\begin{array}{l}\widehat {ACB} = \widehat {ACt} + \widehat {tCB}\\ \Rightarrow \widehat {ACB} = {30^0} + {40^0}\\ \Rightarrow \widehat {ACB} = {70^0}\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 3.25 trang 44 sách bài tập toán 7 - Kết nối tri thức với cuộc sống timdapan.com"







