Bài 3 trang 53 Vở bài tập toán 9 tập 1
Giải bài 3 trang 53 VBT toán 9 tập 1. Đồ thị hàm số y = căn3 x được vẽ bằng compa và thước thẳng ở hình 2...
Đề bài
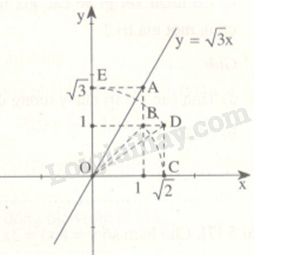
Đồ thị hàm số \(y = \sqrt 3 x\) được vẽ bằng compa và thước thẳng ở hình 2. Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
Phương pháp giải - Xem chi tiết
+) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\): Cho \(x=x_0 \Rightarrow y_0=ax_0\)
Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)
+) Sử dụng định lí Py-ta-go: Tam giác \(\Delta ABC\) vuông tại \(A\) thì \(AB^2+ AC^2 =BC^2\).
Lời giải chi tiết
- Vẽ một hình vuông có độ dài cạnh là 1 đơn vị, có một đỉnh là O, đường chéo OB có độ dài bằng \(\sqrt 2 .\)
- Vẽ cung tròn tâm \(O\), bán kính \(OB\) , ta xác định được điểm \(C\) trên tia \(Ox\), và ta có \(OC = \sqrt 2 .\)
- Vẽ một hình chữ nhật có một đỉnh là O, cạnh \(CD = 1\) và cạnh \(OC = OB =\sqrt 2 \) ta được đường chéo \(OD = \sqrt {C{D^2} + O{C^2}} \)\(= \sqrt {1 + {{\left( {\sqrt 2 } \right)}^2}} = \sqrt 3 .\)
- Vẽ cung tròn tâm \(O\), bán kính \(OD\) , ta xác định được điểm \(E\) trên tia \(Oy\), và ta có \(OE = \sqrt 3 .\)
- Vẽ hình chữ nhật có một đỉnh là O, có một cạnh bằng 1 đơn vị và một cạnh có độ dài bằng \(\sqrt 3 \) ta được điểm \(A\left( {1;\sqrt 3 } \right)\)
- Vẽ đường thẳng đi qua gốc tọa độ O và điểm A ta được đồ thị của hàm số \(y = \sqrt 3 x\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 3 trang 53 Vở bài tập toán 9 tập 1 timdapan.com"







