Giải bài 24 trang 62 sách bài tập toán 8 - Cánh diều
Vẽ đồ thị của các hàm số \(y = - x,y = - x - 1,y = - \frac{1}{3}x,y = \frac{1}{3}x + 2\) trên cùng một mặt phẳng tọa độ.
Đề bài
Vẽ đồ thị của các hàm số \(y = - x,y = - x - 1,y = - \frac{1}{3}x,y = \frac{1}{3}x + 2\) trên cùng một mặt phẳng tọa độ.
Phương pháp giải - Xem chi tiết
Để vẽ đồ thị của hàm số \(y = ax + b\left( {a \ne 0,b \ne 0} \right)\), ta có thể xác định hai điểm \(P\left( {0;b} \right)\) và \(Q\left( { - \frac{b}{a};0} \right)\) rồi vẽ đường thẳng đi qua hai điểm đó.
Lời giải chi tiết
Xét hàm số \(y = - x\). Với \(x = 1\) thì \(y = - 1\), ta được điểm \(A\left( {1; - 1} \right)\) thuộc đồ thị của hàm số \(y = - x\). Vậy đồ thị của hàm số \(y = - x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(A\left( {1; - 1} \right)\).
Xét hàm số \(y = - x - 1\). Với \(x = 0\) thì \(y = - 1\), ta được điểm \(B\left( {0; - 1} \right)\) thuộc đồ thị của hàm số \(y = - x - 1\). Với \(y = 0\) thì \(x = - 1\), ta được điểm \(C\left( { - 1;0} \right)\) thuộc đồ thị của hàm số \(y = - x - 1\). Vậy đồ thị của hàm số \(y = - x - 1\) là đường thẳng đi qua hai điểm \(B\left( {0; - 1} \right)\) và \(C\left( { - 1;0} \right)\).
Tương tự ta có:
Đồ thị của hàm số \(y = \frac{1}{3}x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right)\) và \(D\left( {3;1} \right)\).
Đồ thị của hàm số \(y = \frac{1}{3}x + 2\) là đường thẳng đi qua hai điểm \(E\left( {0;2} \right)\) và \(F\left( { - 6;0} \right)\).
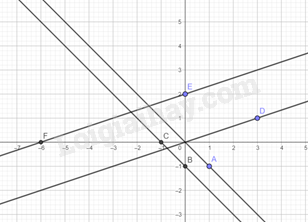
Ta vẽ các đồ thị trên:
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 24 trang 62 sách bài tập toán 8 - Cánh diều timdapan.com"







