Giải bài 2.30 trang 51 SGK Toán 8 - Cùng khám phá
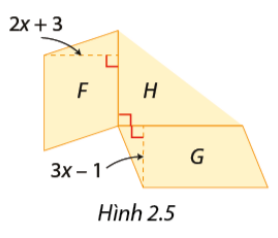
Trong Hình 2.5, hình bình hành F có diện tích là
Đề bài
Trong Hình 2.5, hình bình hành F có diện tích là \(8{x^2} + 14x + 3\) mét vuông và chiều cao là \(2x + 3\) mét. Hình bình hành G có diện tích là \(12{x^2} - 4x\) mét vuông và chiều cao là \(3x - 1\) mét. Tính diện tích của tam giác vuông H theo x.
Phương pháp giải - Xem chi tiết
Áp dụng công thức tính diện tích hình bình hành và tính diện tích tam giác vuông, các phương pháp nhân hai phân thức để tính diện tích tam giác vuông theo x.
Lời giải chi tiết
Ta thấy chiều cao của tam giác vuông H cũng là cạnh đáy của hình bình hành F.
Cạnh đáy của tam giác vuông H cũng là cạnh đáy của hình bình hành G.
Vậy chiều cao của tam giác vuông H là:
\(\frac{{{S_{hbhF}}}}{{{h_{hbhF}}}} = \frac{{8{x^2} + 14x + 3}}{{2x + 3}} = \frac{{\left( {4x + 1} \right)\left( {2x + 3} \right)}}{{2x + 3}} = 4x + 1\)
Cạnh đáy của tam giác vuông H là:
\(\frac{{{S_{hbhG}}}}{{{h_{hbhG}}}} = \frac{{12{x^2} - 4x}}{{3x - 1}} = \frac{{\left( {3x - 1} \right)4x}}{{3x - 1}} = 4x\)
Diện tích tam giác vuông H là:
\(\frac{1}{2}.\left( {4x + 1} \right).4x = \frac{{4x\left( {4x + 1} \right)}}{2} = \frac{{16{x^2} + 4x}}{2} = \frac{{2\left( {8{x^2} + 2x} \right)}}{2} = 8{x^2} + 2x\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 2.30 trang 51 SGK Toán 8 - Cùng khám phá timdapan.com"







