Giải bài 2.12 trang 24 sách bài tập toán 8 - Kết nối tri thức với cuộc sống
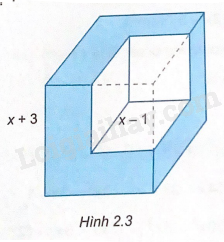
Từ một khối lập phương \(x + 3\)(cm), ta cắt bỏ một khối lập phương có độ dài
Đề bài
Từ một khối lập phương \(x + 3\)(cm), ta cắt bỏ một khối lập phương có độ dài \(x - 1\)(cm) (H.2.3). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
Phương pháp giải - Xem chi tiết
Thể tích phần còn lại bằng thể tích khối lập phương ban đầu trừ đi thể tích khối lập phương cắt bỏ.
Lời giải chi tiết
Do cạnh của khối lập phương ban đầu là \(x + 3\)(cm) nên thể tích của khối lập phương ban đầu là \({\left( {x + 3} \right)^3}\)\(\left( {c{m^3}} \right)\).
Thể tích của khối lập phương cắt đi là \({\left( {x - 1} \right)^3}\)\(\left( {c{m^3}} \right)\).
Thể tích phần còn lại là
\({\left( {x + 3} \right)^3} - {\left( {x - 1} \right)^3}\)
\( = {x^3} + 3.{x^2}.3 + 3.x{.3^2} + {3^3} - \left( {{x^3} - 3.{x^2}.1 + 3.x{{.1}^2} - {1^3}} \right)\)
\( = {x^3} + 9{x^2} + 27x + 27 - {x^3} + 3{x^2} - 3x. + 1\)
\( = \left( {{x^3} - {x^3}} \right) + \left( {9{x^2} + 3{x^2}} \right) + \left( {27x - 3x} \right) + \left( {27 + 1} \right)\)
\( = 12{x^2} + 24x + 28\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 2.12 trang 24 sách bài tập toán 8 - Kết nối tri thức với cuộc sống timdapan.com"







