Giải bài 2.1 trang 18 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho bất phương trình bậc nhất hai ẩn \( - 3x + y < 4.\)

a)      Biểu diễn miền nghiệm của bất phương trình đã cho trên mặt phẳng tọa độ.

b)     Từ đó suy ra miền nghiệm của bất phương trình \( - 3x + y \le 4\) và miền nghiệm của bất phương trình \( - 3x + y \ge 4.\)

Lời giải chi tiết

a) Ta biểu diễn miền nghiệm của bất phương trình như sau:

Vẽ đường thẳng \(d: - 3x + y = 4\) trên mặt phẳng tọa độ \(Oxy.\)

Chọn điểm \(O\left( {0;0} \right)\) là điểm không thuộc đường thẳng \(d\) và thay vào biểu thức \( - 3x + y,\) ta được \( - 3.0 + 0 = 0 < 4.\)

Do đó, miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ \(d\) chứa gốc tọa độ mà (không kể \(d\)₎ (miền không bị gạch).

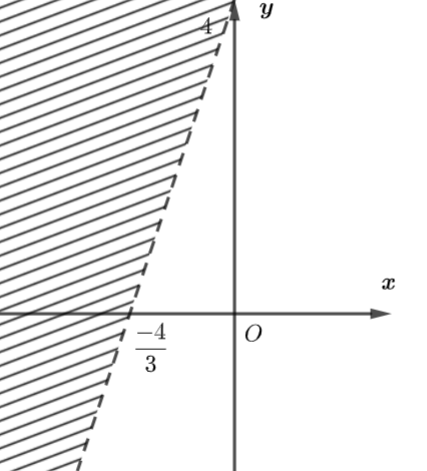
b)  Miền nghiệm của phương trình \( - 3x + y \le 4\) chính là nửa mặt phẳng \(d\) chứa gốc tọa độ.

Miền nghiệm của phương trình \( - 3x + y \ge 4\)chính là nửa mặt phẳng \(d\) không chứa gốc tọa độ (miền bị gạch).