Bài 2.1, 2.2, 2.3 phần bài tập bổ sung trang 83 SBT toán 6 tập 2
Giải bài 2.1, 2.2, 2.3 phần bài tập bổ sung trang 83 sách bài tập toán 6. Nhìn và đọc tên góc, tên đỉnh, tên các cạnh, viết ký hiệu của mỗi góc có trong hình bs.3 ...
Bài 2.1
Nhìn và đọc tên góc, tên đỉnh, tên các cạnh, viết ký hiệu của mỗi góc có trong hình bs.3
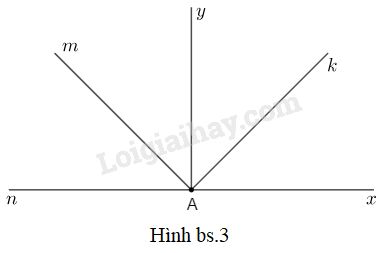
Phương pháp giải:
Sử dụng:
- Góc là hình tạo bởi hai tia chung gốc. Gốc chung là đỉnh của góc. Hai tia là hai cạnh của góc.
- Góc \(xOy\) được kí hiệu là \(\widehat{xOy}\) hoặc \(\widehat{yOx}\).
Giải chi tiết:
Ta lập bảng như sau:
|
Tên góc |
Đỉnh |
Cạnh |
Kí hiệu |
|
Góc \(xAk\) |
\(A\) |
\(Ax, Ak\) |
\(\widehat {xAk}\) |
|
Góc \(xAy\) |
\(A\) |
\(Ax, Ay\) |
\(\widehat { xAy }\) |
|
Góc \(xAm\) |
\(A\) |
\(Ax, Am\) |
\(\widehat { xAm}\) |
|
Góc \(xAn\) |
\(A\) |
\(Ax, An\) |
\(\widehat { xAn }\) |
|
Góc \(kAy\) |
\(A\) |
\(Ak, Ay\) |
\(\widehat { kAy }\) |
|
Góc \(kAm\) |
\(A\) |
\(Ak, Am\) |
\(\widehat { kAm}\) |
|
Góc \(kAn\) |
\(A\) |
\(Ak, An\) |
\(\widehat { kAn }\) |
|
Góc \(yAm\) |
\(A\) |
\(Ay, Am\) |
\(\widehat { yAm}\) |
|
Góc \(yAn\) |
\(A\) |
\(Ay, An\) |
\(\widehat { yAn }\) |
|
Góc \(mAn\) |
\(A\) |
\(Am, An\) |
\(\widehat { mAn}\) |
Bài 2.2
Vẽ hình theo cách diễn đạt bằng lời trong mỗi trường hợp sau đây.
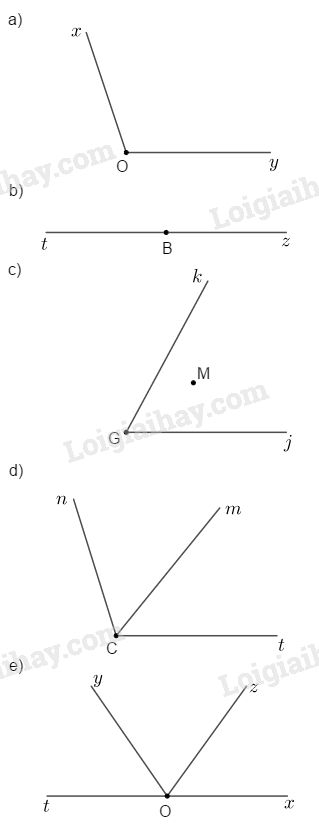
a) Vẽ góc \(xOy\) không phải là góc bẹt;
b) Vẽ góc bẹt \(tBz\);
c) Vẽ góc \(jGk\) và điểm \(M\) nằm bên trong góc đó;
d) Vẽ góc \(nCm\) và \(nCt\) sao cho tia \(Cm\) nằm giữa hai tia \(Cn\) và \(Ct\);
e) Vẽ các góc \(xOy, yOz, zOt\) sao cho tia \(Oz\) nằm trong góc \(xOy\), tia \( Oy\) nằm trong góc \(zOt\) và \(xOt\) là góc bẹt.
Phương pháp giải:
Giải chi tiết:
Bài 2.3
Mỗi câu sau đây đúng hay sai?
a) Hình tạo bởi hai tia là một góc;
b) Hình tạo bởi hai tia phân biệt là một góc;
c) Hình tạo bởi hai tia cắt nhau là một góc;
d) Hình tạo bởi hai tia trùng nhau là một góc;
e) Hình tạo bởi hai tia đối nhau là một góc;
f) Hình tạo bởi hai tia bất kỳ trên một đường thẳng là một góc bẹt;
g) Hình tạo bởi hai tia có nhiều điểm chung (nhưng không trùng nhau) là một góc bẹt;
h) Hình tạo bởi hai tia trùng nhau là một góc bẹt;
i) Khi vẽ hai góc \(xOy\) và \(yOz\) thì \(Oy\) luôn nằm trong góc \(xOz\);
j) Khi vẽ hai góc \(mOn\) và \(nOt\), điểm bất kỳ thuộc tia \( On\) (không trùng với \(O\)) luôn nằm trong góc \(mOt\);
k) Cho góc \(pQr\) (không phải là góc bẹt), điểm \(A\) bất kỳ trên tia \(Qp\), điểm \(B\) bất kỳ trên tia \(Qr\) (\(A\) và \(B\) không trùng với \(Q\)). Điểm \(M\) thuộc đoạn thẳng \(AB\). Khi đó tia \(QM\) luôn nằm trong góc \(pQr\).
Phương pháp giải:
Giải chi tiết:
a) Sai
VD:
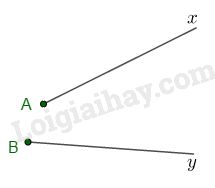
b) Sai
VD:

c) Sai
VD:
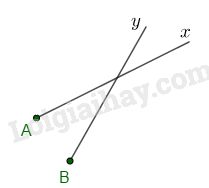
d) Đúng, vì hai tia trùng nhau là hai tia chung gốc.
e) Đúng, vì góc bẹt là góc có hai cạnh là hai tia đối nhau.
f) Sai, vì chưa chắc hai tia nằm trên cùng một đường thẳng đã chung gốc.
VD:

Tia \(AB\) và \(BC\) cùng nằm trên một đường thẳng nhưng hai tia này không tạo thành góc.
g) Sai.
VD:

Tia \(AB\) và tia \(AC\) có nhiều điểm chung nhưng tia \(AB, AC\) không đối nhau nên không tạo thành góc bẹt.
h) Sai, vì góc bẹt là góc có hai cạnh là hai tia đối nhau.
i) Sai.
VD:
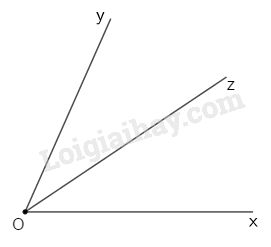
\(Oy\) không nằm trong góc \(xOz\).
j) Sai.
VD:
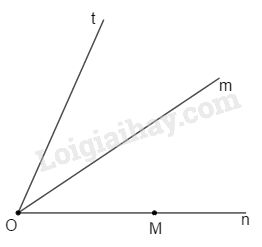
\(M\) thuộc tia \(On\) nhưng \(M\) không nằm trong góc \(mOt\).
k) Đúng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 2.1, 2.2, 2.3 phần bài tập bổ sung trang 83 SBT toán 6 tập 2 timdapan.com"







