Giải bài 19 trang 95 sách bài tập toán 8 - Cánh diều
Cho tam giác nhọn \(ABC\) có ba đường cao \(AM,BN,CP\) cắt nhau tại \(H\). Qua \(B\) kẻ tia \(Bx\) vuông góc với \(AB\).
Đề bài
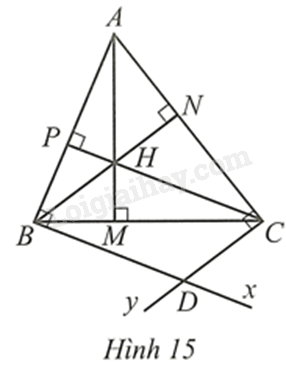
Cho tam giác nhọn \(ABC\) có ba đường cao \(AM,BN,CP\) cắt nhau tại \(H\). Qua \(B\) kẻ tia \(Bx\) vuông góc với \(AB\). Qua \(C\) kẻ tia \(Cy\) vuông góc với \(AC\). Gọi \(D\) là giao điểm của \(Bx\) và \(Cy\) (Hình 15)
a) Chứng minh tứ giác \(BDCH\) là hình bình hành;
b) Tam giác \(ABC\) có điều kiện gì thi ba điểm \(A,D,H\) thẳng hàng?
c) Tìm mối liên hệ giữa góc \(A\) và góc \(D\) của tứ giác \(ABCD\).
d) Giả sử \(H\) là trung điểm của \(AM\). Chứng minh diện tích của tam giác \(ABC\) bằng diện tích của tứ giác \(BHCD\).
Phương pháp giải - Xem chi tiết
Dựa vào dấu hiệu nhận biết của hình bình hành:
- Tứ giác có hai cặp cạnh đối bằng nhau là hình bình hành
- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành
- Tứ giác có hai cặp góc đối bằng nhau là hình bình hành
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
Lời giải chi tiết
a) Ta có: \(\widehat {APC} = \widehat {ABD} = 90^\circ \) và \(\widehat {APC},\widehat {ABD}\) nằm ở vị trí đồng vị nên \(CP//BD\).
Tương tự ta chứng minh được \(BN//CD\).
Tứ giác \(BDCH\) có \(BD//CH,BH//CD\) nên \(BDCH\) là hình bình hành.
b) Để ba điểm \(A,D,H\) thẳng hàng thì \(M\) phải thuộc \(DH\). Mà \(M\) thuộc \(BC\), suy ra \(M\) là giao điểm của \(BC\) và \(DH\).
Do \(BDCH\) là hình bình hành nên hai đường chéo \(BC\) và \(DH\) cắt nhau tại trung điểm của mỗi đường. suy ra \(M\) là trung điểm \(BC\).
Khi đó \(\Delta ABM = \Delta ACM\) (c.g.c). Suy ra \(AB = AC\).
Dễ thấy nếu tam giác \(ABC\) có \(AB = AC\) thì ba điểm \(A,D,H\) thẳng hàng.
Vậy tam giác \(ABC\) cân tại \(A\) thì \(A,D,H\) thẳng hàng.
c) Xét tứ giác \(ABCD\), ta có: \(\widehat {BAC} + \widehat {DBA} + \widehat {CDB} + \widehat {ACD} = 360^\circ \).
Mà \(\widehat {DBA} = \widehat {ACD} = 90^\circ \), suy ra tính được \(\widehat {BAC} + \widehat {CDB} = 3180^\circ \)
Vậy góc \(A\) và góc \(D\)của tứ giác \(ABCD\) là hai góc bù nhau.
d) Do \(H\) là trung điểm của \(AM\) nên \(HM = \frac{1}{2}AM\)
Ta có diện tích tam giác \(ABC\) bằng: \(\frac{1}{2}.AM.BC = HM.BC\).
Ta chứng minh được \(\Delta BCH = \Delta CBD\) (c.c.c.). Suy ra diện tích tứ giác \(BHCD\) bằng 2 lần diện tích tam giác \(BCH\).
Do đó, diện tích tứ giác \(BHCD\) bằng: \(\left( {\frac{1}{2}.HM.BC = HM.BC} \right)\) vạy diện tích tam giác \(ABC\) bằng điệnt tích của tứ giác \(BHCD\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 19 trang 95 sách bài tập toán 8 - Cánh diều timdapan.com"







