Bài 15 trang 103 Vở bài tập toán 8 tập 1
Giải bài 15 trang 103 VBT toán 8 tập 1. Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.
Đề bài
Hình thang \(ABCD\) có đáy \(AB, CD.\) Gọi \(E, F, K\) theo thứ tự là trung điểm của \(AD, BC, BD.\) Chứng minh ba điểm \(E, K, F\) thẳng hàng.
Phương pháp giải - Xem chi tiết
Áp dụng:
- Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Tiên đề Ơclit: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.
Lời giải chi tiết
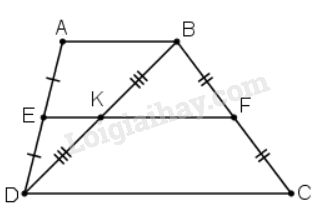

Ta sẽ chứng minh \(KE\) và \(KF\) cùng song song với \(AB\).
\(\Delta ABD\) có \(EA=ED \) và \(KB=KD\) nên EK là đường trung bình. Do đó \(KE // AB\).
\(\Delta BDC\) có: \(FB=FC\) và \( KB=KD\) nên FK là đường trung bình. Do đó \( KF // DC\) nên \( KF // AB\)
Qua điểm \(K\) có hai đường thẳng \(KE\) và \(KF\) cùng \(//AB\) nên theo tiên đề Ơ-clit thì ba điểm \(E, K, F\) thẳng hàng .
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 15 trang 103 Vở bài tập toán 8 tập 1 timdapan.com"







