Bài 13 trang 13 Vở bài tập toán 8 tập 2

Viết phương trình ẩn \(x\) rồi tính \(x\) (mét) trong mỗi hình dưới đây (\(S\) là diện tích của hình): 

LG a

Phương pháp giải:

Công thức tính diện tích hình chữ nhật: \(S=a\times b\)

Trong đó: \(S\) là diện tích hình chữ nhật 

               \(a\) là chiều dài hình chữ nhật

               \(b\) là chiều rộng hình chữ nhật

- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).

+ Tìm \(x\)

Lời giải chi tiết:

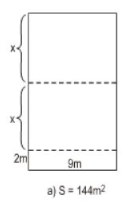
\(S = 144\) \((m^2)\) đúng bằng tổng diện tích của ba hình chữ nhật.

Từ đó ta có phương trình \(9.2+9.x+9.x=144\)

Giải phương trình này, ta được \(x = 7\,(m)\)

Chú ý: \(9.2+9.x+9.x=144\)

\(⇔18 x + 18 =  144\)

\(⇔18 x = 144 - 18\)

\(⇔18x = 126\)

\(\Leftrightarrow x=126:18\) 

\(⇔ x = 7\)

LG b

Phương pháp giải:

Công thức tính diện tích hình chữ nhật: \(S=a\times b\)

Trong đó: \(S\) là diện tích hình chữ nhật

               \(a\) là chiều dài hình chữ nhật

               \(b\) là chiều rộng hình chữ nhật 

Công thức tính diện tích tam giác \(S = \dfrac{1}{2}a.h\) 

\(a\) là cạnh của tam giác, \(h\) là chiều cao tương ứng với cạnh \(a\) của tam giác.

- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).

+ Tìm \(x\) 

Lời giải chi tiết:

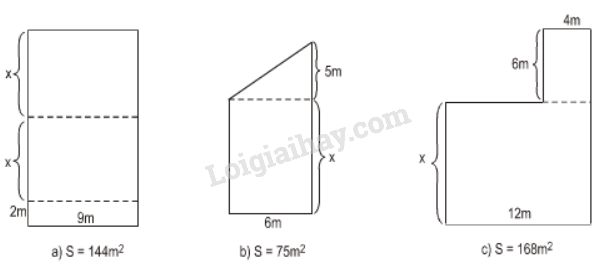
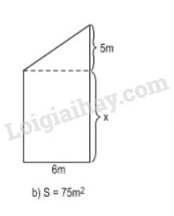
 \(S=75\) \((m^2)\) đúng bằng tổng diện tích của hình chữ nhật và hình tam giác.

Từ đó ta có phương trình \(6.x+\dfrac{1}{2}.6.5=75\)

Giải phương trình này, ta được \(x = 10\;(m)\).

Chú ý: \(6.x+\dfrac{1}{2}.6.5=75\)

\(\begin{array}{l}
\Leftrightarrow 6x + 15 = 75\\
\Leftrightarrow 6x = 75 - 15\\
\Leftrightarrow 6x = 60\\ 
\Leftrightarrow x = 60:6\\
\Leftrightarrow x = 10
\end{array}\)

LG c

Phương pháp giải:

Công thức tính diện tích hình chữ nhật: \(S=a\times b\)

Trong đó: \(S\) là diện tích hình chữ nhật

               \(a\) là chiều dài hình chữ nhật

               \(b\) là chiều rộng hình chữ nhật  

- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:

+ Quy đồng mẫu hai vế và khử mẫu.

+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).

+ Tìm \(x\)

Lời giải chi tiết:

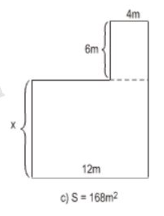
\(S=168\) \((m^2)\) đúng bằng tổng diện tích của hai hình chữ nhật.

Từ đó ta có phương trình \(12.x+4.6=168\)

Giải phương trình này, ta được \(x = 12\,(m).\)

Chú ý: \(12.x+4.6=168\)

\(12x + 24 = 168\)

\( \Leftrightarrow 12x = 168 - 24\)

\( \Leftrightarrow 12x = 144\)

\( \Leftrightarrow x = 144:12\)

\(\Leftrightarrow x = 12\)