Bài 12.3 phần bài tập bổ sung trang 13 SBT toán 8 tập 1

Đề bài

Cho hai đa thức \(A=2{x^4} - 10{x^3} + 3{x^2} - 3x + 2;\)\(B = 2{x^2} + 1\).

Tìm đa thức dư \(R\) trong phép chia \(A\) cho \(B\) rồi viết \(A= B.Q + R\)

Lời giải chi tiết

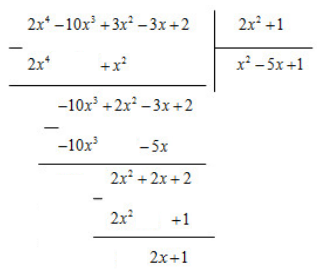
Từ đó ta có thương \(Q=x^2-5x+1\) và phần dư \(R=2x+1\)

Vậy: \(2{x^4} - 10{x^3} + 3{x^2} - 3x + 2\)\(=\left( {2{x^2} + 1} \right)\left( {{x^2} - 5x + 1} \right) + 2x + 1\)