Giải Bài 12 trang 107 sách bài tập toán 7 tập 1 - Cánh diều

Đề bài

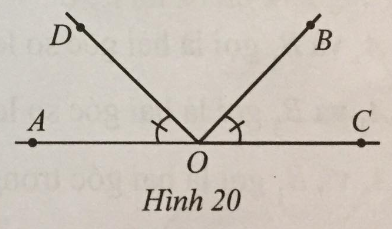
Ở Hình 20 có hai góc AOB và BOC là hai góc kề bù, \(\widehat {AOB} = 3\widehat {BOC}\), \(\widehat {AOD} = \widehat {BOC}\).

a) Tính số đo góc BOC.                                                   

b) Tia OB có là tia phân giác của góc COD hay không?

Lời giải chi tiết

a) Ta có:

\(\begin{array}{l}\widehat {AOB} + \widehat {BOC} = \widehat {AOC} = 180^\circ  \to 3\widehat {BOC} + \widehat {BOC} = 180^\circ \\ \to 4\widehat {BOC} = 180^\circ  \Rightarrow \widehat {BOC} = \widehat {AOD} = 180^\circ :4 = 45^\circ \end{array}\)

Vậy \(\widehat {BOC} = 45^\circ \).

b) Ta có: \(\widehat {BOD} = \widehat {AOC} - \widehat {AOD} - \widehat {BOC} = 180^\circ  - 45^\circ  - 45^\circ  = 90^\circ \).

Mà \(\widehat {BOC} = 45^\circ  < \widehat {BOD} = 90^\circ \) nên tia OB không là tia phân giác của góc COD.