Bài 1.16 trang 24 SBT hình học 11
Giải bài 1.16 trang 24 sách bài tập hình học 11. Trong mặt phẳng Oxy cho các điểm A(3;3), B(0;5), C(1;1) và đường thẳng d có phương trình 5x-3y+15=0. Hãy xác định tọa độ các đỉnh của tam giác A’B’C’ và phương trình của đường thẳng d' theo thứ tự là ảnh của tam giác ABC và đường thẳng d qua phép quay tâm O, góc quay 90°.
Đề bài
Trong mặt phẳng \(Oxy\) cho các điểm \(A(3;3)\), \(B(0;5)\), \(C(1;1)\) và đường thẳng \(d\) có phương trình \(5x-3y+15=0\). Hãy xác định tọa độ các đỉnh của tam giác \(A’B’C’\) và phương trình của đường thẳng \(d’\) theo thứ tự là ảnh của tam giác \(ABC\) và đường thẳng \(d\) qua phép quay tâm \(O\), góc quay \({90}^o\).
Phương pháp giải - Xem chi tiết
Sử dụng định nghĩa:
Cho \(O\) và góc lượng giác \(\alpha\). Phép biến hình biến \(O\) thành chính nó, biến mỗi điểm \(M\) khác \(O\) thành điểm \(M’\) sao cho \(OM’=OM\) và góc lượng giác \((OM;OM’)\) bằng \(\alpha\) được gọi là phép quay tâm \(O\) góc \(\alpha\).
Lời giải chi tiết
Gọi \(Q_{(O,{90}^o)}\) là phép quay tâm \(O\), góc quay \({90}^o\).
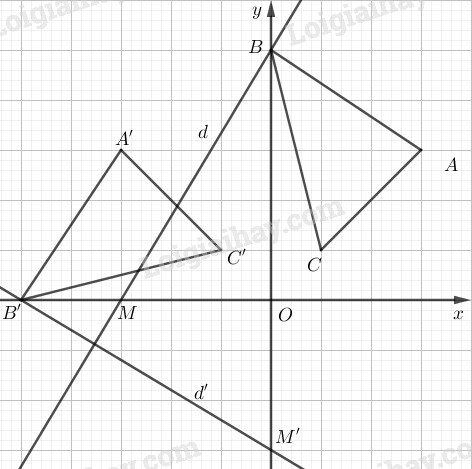
Điểm \(A’(-3;3)\), \(B’(-5;0)\), \(C’(-1;1)\).
Đường thẳng \(d\) đi qua \(B\) và \(M(-3;0)\).
Ta có \(M’=Q_{(O,{90}^o)}(M)=(0;-3)\) nên \(d’\) là đường thẳng \(B’M’\).
\(\overrightarrow {B'M'} = \left( {5; - 3} \right) \Rightarrow \overrightarrow {{n_{B'M'}}} = \left( {3;5} \right)\) là VTPT của B'M'.
Mà B'M' đi qua B'(-5;0) nên B'M': 3(x+5)+5(y-0)=0 hay 3x+5y+15=0.
Vậy d' có phương trình \(3x+5y+15=0\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 1.16 trang 24 SBT hình học 11 timdapan.com"







