Bài 11 trang 124 Vở bài tập toán 6 tập 1

Đề bài

Lấy bốn điểm \(A,B,C,D\) trong đó không có \(3\) điểm nào thẳng hàng. Kẻ các đường  thẳng đi qua các cặp điểm. Có tất cả bao nhiêu đường  thẳng? Đó là những đường thẳng nào? 

Lời giải chi tiết

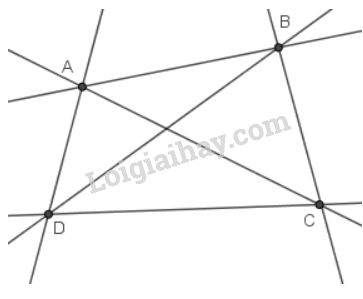
Em hãy so sánh cách làm của ba bạn sau (xem hình vẽ)

Bạn An: Cứ qua hai điểm vẽ một đường thẳng rồi đếm số đường thẳng vẽ được. Bạn đếm được \(6\) đường thẳng (phân biệt), đó là:

\(AB, AC, AD, CB,CD,BD\).

Bạn Bình: Vừa vẽ, vừa đếm như sau:

Kẻ đường thẳng qua \(A,B\); qua \(A,C\); qua \(A,D\) được \(3\) đường thẳng.

Kẻ đường thẳng qua \(B,C\); qua \(B,D\) được \(2\) đường thẳng.

Kẻ đường thẳng qua \(C,D\) được \(1\) đường thẳng.

Tất cả có \(6\) đường thẳng.

Bạn Chính: Cứ qua mỗi điểm vẽ ba đường thẳng đi qua ba điểm còn lại bằng bút màu xanh. Đường thẳng nào trùng với đường thẳng màu xanh thì được vẽ bằng màu tím.

Qua \(A\), vẽ đường thẳng qua ba điểm còn lại, được ba đường thẳng màu xanh là \(AB, AC, AD\).

Qua \(B\), vẽ đường thẳng qua ba điểm còn lại, được ba đường thẳng là \(BA,BC,BD\) trong đó \(BA\) được vẽ màu tím vì trùng với \(AB.\)

Qua \(C\), vẽ đường thẳng qua ba điểm còn lại, được ba đường thẳng là \(CB,CD,CA\) trong đó \(CB,CA\) được vẽ màu tím.

Qua \(D\), vẽ đường thẳng qua ba điểm còn lại, được ba đường thẳng là \(DA,DB,DC\) bằng màu tím.

Như vậy, có \(12\) đường thẳng tất cả \((4\times 3=12)\) nhưng mỗi đường thẳng được vẽ hai lần (màu xanh và màu tím), suy ra tổng số đường thẳng (phân biệt) là \(12:2=6\) đường thẳng.