Bài 11 trang 119 Vở bài tập toán 8 tập 2
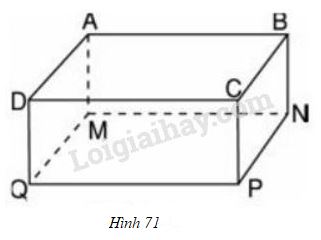
Giải bài 11 trang 119 VBT toán 8 tập 2. Viết công thức tính thể tích của hình hộp chữ nhật ABCD.MNPQ (h71)...
LG a
Viết công thức tính thể tích của hình hộp chữ nhật \(ABCD.MNPQ\) (h71)
Phương pháp giải:
Áp dụng công thức tính thể tích hình hộp chữ nhật: \(V = a.b.c\), trong đó \( a,\, b, \, c\) là các kích thước của hình hộp chữ nhật;
hay thể tích = chiều dài \( \times\) chiều rộng \( \times\) chiều cao.
Lời giải chi tiết:
\({V_{ABCD.MNPQ}} = MN.{\rm{ }}NP.{\rm{ }}NB\)
LG b
Điền số thích hợp vào các ô trống ở bảng sau:
|
Chiều dài |
22 |
18 |
15 |
20 |
|
Chiều rộng |
14 |
|
|
|
|
Chiều cao |
5 |
6 |
8 |
|
|
Diện tích một đáy |
|
90 |
|
260 |
|
Thể tích |
|
|
1320 |
2080 |
Phương pháp giải:
Giả sử \( a\) là chiều dài, \( b\) là chiều rộng và \( c\) là chiều cao.
Ta áp dụng các công thức sau :
\(V = a.b.c\); \(b= V :( a.c)\);
\( S_{\mbox{1 đáy}} = a.b\);
\(b = S_{\mbox{1 đáy}}: a\); \(c= V :S_{\mbox{1 đáy}}\);
Lời giải chi tiết:
+ Hình hộp chữ nhật với các kích thước ở cột 1:
Diện tích một đáy là: \(22 . 14 = 308\)
Thể tích là: \(22. 14 . 5 = 1540\)
+ Hình hộp chữ nhật với các kích thước ở cột 2:
Chiều rộng là: \(90 : 18 = 5\)
Thể tích là: \(18 . 5 . 6 = 90 . 6 = 540\)
+ Hình hộp chữ nhật với các kích thước ở cột 3:
Chiều rộng là: \(1320 : (15 . 8) = 11\)
Diện tích một đáy là: \(15 . 11 = 165\)
+ Hình hộp chữ nhật với các kích thước ở cột 4:
Chiều rộng là: \(260 : 20 = 13\)
Chiều cao là: \(2080 : 260 = 8\)
Ta có kết quả chung như bảng sau:
|
Chiều dài |
22 |
18 |
15 |
20 |
|
Chiều rộng |
14 |
5 |
11 |
13 |
|
Chiều cao |
5 |
6 |
8 |
8 |
|
Diện tích một đáy |
308 |
90 |
165 |
260 |
|
Thể tích |
1540 |
540 |
1320 |
2080 |
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 11 trang 119 Vở bài tập toán 8 tập 2 timdapan.com"