Giải bài 10.14 trang 122 SGK Toán 8 tập 2 - Kết nối tri thức
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre
Đề bài
Người ta làm mô hình kim tự tháp ở cổng vào của bảo tàng Louvre. Mô hình có dạng hình chóp tứ giác đều, chiều cao 21 m, độ dài cạnh đáy là 34 m
a) Tính thể tích hình chóp
b) Tính tổng diện tích các tấm kính để phủ kín bốn mặt bên hình chóp này
Phương pháp giải - Xem chi tiết
- Vẽ hình kim tự tháp để minh họa.
- Áp dụng công thức tính thể tích hình chóp.
- Tổng diện tích các tâm kính để phủ kín bốn mặt bên hình chóp là diẹn tích xung quanh của hình chóp.
Lời giải chi tiết
- Có hình vẽ minh họa cho kim tự tháp
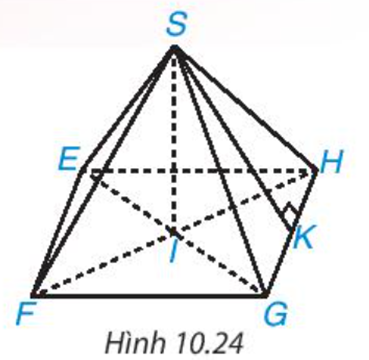
a) Diện tích cạnh đáy là: 34.34=1156 (m2)
- Thể tích hình chóp là:
\(V = \frac{1}{3}.S.h = \frac{1}{3}.1156.21 = 8092\left( {{m^3}} \right)\)
b) Có tam giác SIK cân => KG=KH (m)
- Xét tam giác EHG có: IE=IG, KH=KG
=> IK là đường trung bình của tam giác GEH
=> IK // EH và IK=34:2=17 (m)
- Vì SI là đường cao của hình chóp tứ giác đều => SI vuông góc với IK
- Xét tam giác SIK vuông tại I, có:
\(S{K^2} = S{I^2} + I{K^2} = {21^2} + {17^2} = 730\)
SK= \(\sqrt {730} \) (m)
- Chu vi của hình vuông EFGH là: (34.4):2=68 (m)
Vậy \({S_{xq}} = p.d = 68.\sqrt {730} = 68\sqrt {730} \left( {{m^2}} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải bài 10.14 trang 122 SGK Toán 8 tập 2 - Kết nối tri thức timdapan.com"







