Bài 10 trang 88 Vở bài tập toán 9 tập 1
Giải bài 10 trang 88 VBT toán 9 tập 1. Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Toa DI và tia CB cắt nhau ở K...
Đề bài
Cho hình vuông ABCD. Gọi I là một điểm nằm giữa A và B. Tia DI và tia CB cắt nhau ở K. kẻ đường thẳng qua D, vuông góc với DI. Đường thẳng này cắt đường thẳng BC tại L. Chứng minh rằng:
a) Tam giác DIL là một tam giác cân
b) Tổng \(\dfrac{I}{{D{I^2}}} + \dfrac{I}{{D{K^2}}}\) không dổi khi I thay đổi trên cạnh AB.
Phương pháp giải - Xem chi tiết
- Vẽ hình theo các giả thiết đã cho.
- Áp dụng hệ thức : \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}\)
Lời giải chi tiết
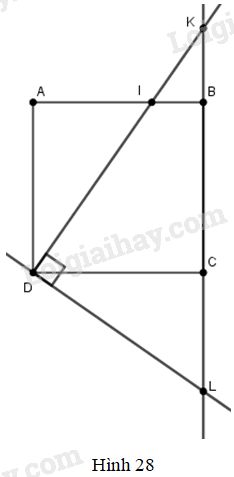
a) Hai tam giác vuông DAI và DCL có \(DA = DC\) (là hai cạnh của hình vuông \(ABCD\));\(\widehat {ADI} = \widehat {CDL}\) (cùng phụ với góc \(\widehat {CDI}\)) nên chúng bằng nhau.
Suy ra \(DI = DL\)
Tam giác \(DIL\) có hai cạnh bên bằng nhau nên nó là một tam giác cân.
b) Theo câu a) ta có :
\(\dfrac{1}{{D{I^2}}} + \dfrac{1}{{D{K^2}}} = \dfrac{1}{{D{L^2}}} + \dfrac{1}{{D{K^2}}}\) (1)
Mặt khác, tam giác vuông \(DKL\) có \(DC\) là đường cao ứng với cạnh huyền nên
\(\dfrac{1}{{D{L^2}}} + \dfrac{1}{{D{K^2}}} = \dfrac{1}{{D{C^2}}}\) (2)
Từ (1) và (2) suy ra
\(\dfrac{1}{{D{I^2}}} + \dfrac{1}{{D{K^2}}} = \dfrac{1}{{D{C^2}}}\)
Vì \(DC\) là cạnh của hình vuông \(ABCD\) đã cho nên độ dài của \(DC\) không đổi, tức là \(\dfrac{1}{{D{I^2}}} + \dfrac{1}{{D{K^2}}} = \dfrac{1}{{D{C^2}}}\) không đổi khi \(I\) thay đổi trên cạnh \(AB.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 10 trang 88 Vở bài tập toán 9 tập 1 timdapan.com"







