Đề thi vào lớp 6 môn Toán trường THCS Lê Văn Thiêm năm 2024

Đề thi

PHÒNG GD-ĐT HÀ TĨNH ĐỀ CHÍNH THỨC

BÀI KIỂM TRA ĐÁNH GIÁ NĂNG LỰC Tuyển sinh vào lớp 6, trường THCS Lê Văn Thiêm Năm học 2024-2025 Thời gian làm bài: 35 phút (không kể thời gian phát đề)

A. PHẦN TRẮC NGHIỆM (7 điểm):

Học sinh ghi đáp án đúng (A,B,C hoặc D) từ câu 1 đến câu 14 vào tờ giấy kiếm tra)

Câu 1. 3 giờ 45 phút = … giờ. Số thập phân thích hợp điền vào chỗ chấm (…) là:

A. 3,25 giờ

B. 3,75 giờ

C. 3,45 giờ

D. 3,075 giờ

Câu 2. Phân số $\frac{{65}}{{10}}$ gấp số 0,65 mấy lần?

A. 10 lần

B. 0,1 lần

C. 100 lần

D. 1 000 lần

Câu 3. Hai số a và b có 𝑎 – 𝑏 = 45,9 và $\frac{a}{b}$= $\frac{5}{2}$. Vậy số a là:

A. 67,5

B. 66,5

C. 3,06

D. 76,5

Câu 4. Một hình tròn có diện tích là 12,56 cm². Chu vi của hình tròn đó là:

A. 12,56 cm

B. 6,28 cm

C. 125,6 cm

D. 50,24 cm

Câu 5. Hai số có trung bình cộng là 13,9 và hiệu hai số là 4,8 . Số bé là:

A. 16,3

B. 12,5

C. 11,5

D. 4,55

Câu 6. Một bể nước dạng hình hộp chữ nhật có thề tích là 3,6 m³, chiều dài 2 m, chiều rộng 1,5 m. Vậy chiều cao của bể nước đó là:

A. 1,8 m

B. 0,12 m

C. 12 m

D. 1,2 m

Câu 7. Nếu 6 người cùng làm một công việc thì xong trong 15 ngày. Biết mức làm của mỗi người đều như nhau thì muốn làm xong công việc đó trong 10 ngày cần phải bổ sung thêm số người là:

A. 4 người

B. 5 người

C. 3 người

D. 9 người

Câu 8. Biết 15%  của a là 4,5 . Số a là:

A 30

B. 3

C. 300

D. 67.5

Câu 9. Lúc 6 giờ sáng, một xe tải đi từ A để đến B với vận tốc trung bình 56 km/h. Lúc 7 giờ sáng cùng ngày, một xe khách đi từ B đến A với vận tốc trung bình 60 km/h. Hỏi hai xe gặp nhau lúc mây giờ? (biết rằng quãng đường AB dài 346 km).

A. 9 giờ 25 phút

B. 9 giờ 30 phút

C. 8 giờ 25 phút

D. 8 giờ 30 phút

Câu 10. Diện tích của một hình chữ nhật thay đổi thế nào nếu đồng thời tăng chiều dài thêm 20% và giảm chiều rộng đi 10% độ dài của nó?

A. Diện tích tăng thêm 10%

B. Diện tích tăng thêm 8%

C. Diện tích tăng thêm 15%

D. Diện tích tăng thêm 0,8%

Câu 11. Trên một đoạn đường thẳng có độ dài 1,5 km người ta trồng cây bóng mát hai bên đường. Biết rằng cứ hai cây liền nhau đều cách nhau 6 m và hai bên đầu đường đều trồng cây. Hỏi người ta đã trồng tất cả bao nhiêu cây trên đoạn đường đó?

A. 251

B. 250

C. 502

D. 500

Câu 12. Hiện nay, tuổi mẹ gấp 5 lần tuồi con. Khi tuổi con bằng tuổi mẹ hiện nay thì tồng số tuổi của hai mẹ con là 84 tuổi. Tuổi con hiện nay là:

A. 5 tuổi

B. 4 tuổi

C. 7 tuổi

D. 6 tuổi

Câu 13. Có bao nhiêu số tự nhiên khác 0 nhỏ hơn 1 000 chia hết cho 3 nhưng không chia hết cho 5?

A. 133

B. 268

C. 267

D. 266

Câu 14. Số tiếp theo của dãy số 4; 6; 10; 14; 22; 26; 34; … là:

A. 46

B. 38

C. 36

D. 44

B. PHẦN TỰ LUẬN (3 điểm):

Câu 15.

a) Tính bằng cách hơp lý: $8\frac{{14}}{{17}} + (6\frac{3}{{17}} - 5\frac{2}{3})$

b) Tìm x, biết: 6 + 7 + 8 + 9 + … + 𝑥 = 195 (các số hạng là các số tự nhiên liên tiếp)

Câu 16. Cho hình vuông ABCD. Trên AB lấy điểm M sao cho AM=MB, nối M với D, M với C.

a) Hỏi diện tích hình tam giác DMC gấp mấy lần diện tích hình tam giác DMA?

b) AC cắt MD tại N. Biết diện tích tam giác AND là 5 cm². Tính diện tích hình vuông ABCD.

--- HẾT ---

---

Đáp án

HƯỚNG DẪN GIẢI CHI TIẾT

A. PHẦN TRẮC NGHIỆM (7 điểm):

1. B	2. A	3. D	4. A	5. C	6. D	7. C
8. A	9. B	10. B	11. C	12. D	13. C	14. B

 

Câu 1. 3 giờ 45 phút = … giờ. Số thập phân thích hợp điền vào chỗ chấm (…) là:

A. 3,25 giờ

B. 3,75 giờ

C. 3,45 giờ

D. 3,075 giờ

Phương pháp

Áp dụng cách đổi: 1 phút = $\frac{1}{{60}}$ giờ

Lời giải

45 phút = $\frac{{45}}{{60}}$= $\frac{3}{4}$=$\frac{{75}}{{100}}$= 0,75 giờ

3 giờ 45 phút = 3,75 giờ

Đáp án: B

Câu 2. Phân số $\frac{{65}}{{10}}$ gấp số 0,65 mấy lần?

A. 10 lần

B. 0,1 lần

C. 100 lần

D. 1 000 lần

Phương pháp

Để xem phân số $\frac{{65}}{{10}}$ gấp số 0,65 bao nhiêu lần, ta thực hiện phép tính  $\frac{{65}}{{10}}$ : 0,65

Lời giải

$\frac{{65}}{{10}}$ : 0,65 = $\frac{{65}}{{10}}$: $\frac{{65}}{{100}}$ = $\frac{{65}}{{10}}$ × $\frac{{100}}{{65}}$ = $\frac{{65 \times 100}}{{10 \times 65}}$ = $\frac{{65 \times 10 \times 10}}{{10 \times 65}}$ = 10

Đáp án: A

Câu 3. Hai số a và b có 𝑎 – 𝑏 = 45,9 và $\frac{a}{b}$= $\frac{5}{2}$. Vậy số a là:

A. 67,5

B. 66,5

C. 3,06

D. 76,5

Phương pháp

Vì a là số bị trừ nên a là số lớn.

Bài toán tìm hai số khi biết hiệu và tỉ số của hai số đó

Số lớn = (Hiệu : hiệu số phần bằng nhau) × số phần của số lớn

Lời giải

Số a là: 45,9 : (5 - 2) × 5 = 76,5

Đáp án: D

Câu 4. Một hình tròn có diện tích là 12,56 cm². Chu vi của hình tròn đó là:

A. 12,56 cm

B. 6,28 cm

C. 125,6 cm

D. 50,24 cm

Phương pháp

Diện tích của hình tròn = bán kính × bán kính × 3,14

Chu vi của hình tròn = bán kính × 2 × 3,14.

Lời giải

Tích bán kính của hình tròn là: 12,56 : 3,14 = 4

Vì 2 × 2 = 4. Nên bán kính của hình tròn là: 2 cm

Chu vi của hình tròn là: 2 × 2 × 3,14 = 12,56 cm

Đáp án: A

Câu 5. Hai số có trung bình cộng là 13,9 và hiệu hai số là 4,8 . Số bé là:

A. 16,3

B. 12,5

C. 11,5

D. 4,55

Phương pháp

Tổng của hai số là: 13,9 × 2 = 27,8

Số bé là: (27,8 – 4,8) : 2 = 11,5

Lời giải

Tổng của hai số = Trung bình cộng × 2

Số bé = (tổng – hiệu) : 2

Đáp án: C

Câu 6. Một bể nước dạng hình hộp chữ nhật có thề tích là 3,6 m³, chiều dài 2 m, chiều rộng 1,5 m. Vậy chiều cao của bể nước đó là:

A. 1,8 m

B. 0,12 m

C. 12 m

D. 1,2 m

Phương pháp

Chiều cao hình hộp chữ nhật = Thể tích : Chiều dài : Chiều rộng

Lời giải

Chiều cao hình hộp chữ nhật là: 3,6 : 2 : 1,5 = 1,2 m

Đáp án: D

Câu 7. Nếu 6 người cùng làm một công việc thì xong trong 15 ngày. Biết mức làm của mỗi người đêu như nhau thì muốn làm xong công việc đó trong 10 ngày cần phải bổ sung thêm số người là:

A. 4 người

B. 5 người

C. 3 người

D. 9 người

Phương pháp

- Số ngày một người làm xong công việc = số người ban đầu × số ngày

- Số người để làm xong công việc đó trong 10 ngày = Số ngày một người làm xong công việc : 10

- Số người cần phải bổ sung thêm = Số người để làm xong công việc đó trong 10 ngày - số người ban đầu

Lời giải

Một người làm xong công việc trong số ngày là:

6 × 15 = 90 (ngày)

Muốn làm xong công việc đó trong 10 ngày thì cần số người là:

90 : 10 = 9 (người)

Muốn làm xong công việc đó trong 10 ngày thì cần phải bổ sung thêm số người là:

9 – 6 = 3 (người)

Đáp án: C

Câu 8. Biết 15% của a là 4,5. Số a là:

A 30

B. 3

C. 300

D. 67.5

Phương pháp

Muốn tìm A khi biết b% của A, ta A chia cho b rồi nhân với 100 hoặc lấy A nhân với 100 rồi chia cho b

Lời giải

Số a là: 4,5 : 15 × 100 = 30

Đáp án: A

Câu 9. Lúc 6 giờ sáng, một xe tải đi từ A để đến B với vận tốc trung bình 56 km/h. Lúc 7 giờ sáng cùng ngày, một xe khách đi từ B đến A với vận tốc trung bình 60 km/h. Hỏi hai xe gặp nhau lúc mây giờ? (biết rằng quãng đường AB dài 346 km).

A. 9 giờ 25 phút

B. 9 giờ 30 phút

C. 8 giờ 25 phút

D. 8 giờ 30 phút

Phương pháp

Quãng đường = Vận tốc × Thời gian

Thời gian = Quãng đường : Vận tốc

Lời giải

Lúc 6 giờ sáng, một xe tải đi từ A để đến B với vận tốc trung bình 56 km/h. Lúc 7 giờ sáng cùng ngày, một xe khách đi từ B đến A với vận tốc trung bình 60 km/h. Hỏi hai xe gặp nhau lúc mây giờ? (biết rằng quãng đường AB dài 346 km).

Đến 7 giờ sáng, xe tải đi được quãng đường là:

56 × (7 – 6) = 56 (km)

Đến 7 giờ sáng, xe tải đi được quãng đường là:

56 × (7 – 6) = 56 (km)

Quãng đường còn lại mà xe tải cần đi để đến B là:

346 – 56 = 290 (km)

Tổng vận tốc của 2 xe là:

56 + 60 = 116 (km/h)

Thời gian để hai xe gặp nhau là:

290 : 116 = 2,5 (giờ) = 2 giờ 30 phút

Hai xe gặp nhau lúc: 7 giờ + 2 giờ 30 phút = 9 giờ 30 phút

Đáp án: B

Câu 10. Diện tích của một hình chữ nhật thay đổi thế nào nếu đồng thời tăng chiều dài thêm 20% và giảm chiều rộng đi 10% độ dài của nó?

A. Diện tích tăng thêm 10%

B. Diện tích tăng thêm 8%

C. Diện tích tăng thêm 15%

D. Diện tích tăng thêm 0,8%

Phương pháp

Diện tích hình chữ nhật = Chiều dài × Chiều rộng

Lời giải

Chiều dài hình chữ nhật sau khi tăng 20% ứng với: 100% + 20% = 120% (chiều dài ban đầu)

Chiều rộng hình chữ nhật sau khi giảm 10% ứng với: 100% - 10% = 90% (chiều rộng ban đầu)

Diện tích sau chiều dài tăng 20% và chiều rộng giảm 10% ứng với: 120% × 90% = 108% (diện tích ban đầu)

=> diện tích đã giảm đi 108% - 100% = 8%

Đáp án: B

Câu 11. Trên một đoạn đường thẳng có độ dài 1,5 km người ta trồng cây bóng mát hai bên đường. Biết rằng cứ hai cây liền nhau đều cách nhau 6 m và hai bên đầu đường đều trồng cây. Hỏi người ta đã trồng tất cả bao nhiêu cây trên đoạn đường đó?

A. 251

B. 250

C. 502

D. 500

Phương pháp

Trên một đoạn đường thẳng có độ dài 1,5 km người ta trồng cây bóng mát hai bên đường. Biết rằng cứ hai cây liền nhau đều cách nhau 6 m và hai bên đầu đường đều trồng cây. Hỏi người ta đã trồng tất cả bao nhiêu cây trên đoạn đường đó?

Lời giải

Đổi 1,5 km = 1 500 m

Vì cứ hai cây liền nhau đều cách nhau 6 m và hai bên đầu đường đều trồng cây nên người ta đã trồng tất cả số cây trên đoạn đường đó là:

(1 500 : 6 + 1) × 2 = 502 cây

Đáp án: C

Câu 12. Hiện nay, tuổi mẹ gấp 5 lần tuồi con. Khi tuổi con bằng tuổi mẹ hiện nay thì tồng số tuổi của hai mẹ con là 84 tuổi. Tuổi con hiện nay là:

A. 5 tuổi

B. 4 tuổi

C. 7 tuổi

D. 6 tuổi

Phương pháp

- Tìm tổng số phần bằng nhau và tìm giá trị của 1 phần.

- Tuổi con = Giá trị của một phần × số phần của tuổi con

Lời giải

Sơ đồ tuổi con và tuổi mẹ hiện nay:

Vì hiệu số tuổi của mẹ và con là không thay đổi. Nên ta có sơ đồ tuổi con và tuổi mẹ lúc tuổi con bằng tuổi mẹ hiện nay:

Tổng số phần bằng nhau là: 14 phần

Tuổi của con là: 84 : 14 = 6 (tuổi)

Đáp án: D

Câu 13. Có bao nhiêu số tự nhiên khác 0 nhỏ hơn 1 000 chia hết cho 3 nhưng không chia hết cho 5?

A. 133

B. 268

C. 267

D. 266

Phương pháp

Tìm tất cả các số tự nhiên khác 0 nhỏ hơn 1 000 và chia hết cho 3

Tìm tất cả các số tự nhiên khác 0 nhỏ hơn 1 000 và chia hết cho cả 3 và 5

Số số tự nhiên khác 0 nhỏ hơn 1 000 chia hết cho 3 nhưng không chia hết cho 5 = tất cả số tự nhiên khác 0 nhỏ hơn 1 000 và chia hết cho 3 - tất cả các số tự nhiên khác 0 nhỏ hơn 1 000 và chia hết cho cả 3 và 5

Lời giải

Các số chia hết cho 3 khác 0 và bé hơn 1000 thuộc dãy số 3 ; 6 ; 9 ; 12 ;……..; 999.

Từ 0 đến 1 000 có số số tự nhiên chia hết cho 3 là:

(999 – 3) : + 1 = 333

Số số tự nhiên chia hết cho 3 và 5 sẽ chia hết cho 15. Các số chia hết cho 15 khác 0 và bé hơn 1000 thuộc dãy số 15 ; 30 ;……..; 990.

Từ 0 đến 1 000 có số số tự nhiên chia hết cho 15 là:

(990 – 15) : 15 + 1 = 66 số

Số số tự nhiên khác 0 nhỏ hơn 1 000 chia hết cho 3 nhưng không chia hết cho 5 là:

333 – 66 = 267 số

Đáp án: C

Câu 14. Số tiếp theo của dãy số 4; 6; 10; 14; 22; 26; 34; … là:

A. 46

B. 38

C. 36

D. 44

Phương pháp

Tìm quy luật của dãy số

Lời giải

4 = 2 × 2

6 = 2 × 3

10 = 2 × 5

14 = 2 × 7

22 = 2 × 11

26 = 2 × 13

34 = 2 × 17

Vậy số tiếp theo của dãy số là: 2 × 19 = 38

Đáp án: B

B. PHẦN TỰ LUẬN (3 điểm):

Câu 15.

a) Tính bằng cách hơp lý: $8\frac{{14}}{{17}} + (6\frac{3}{{17}} - 5\frac{2}{3})$

b) Tìm x, biết: 6 + 7 + 8 + 9 + … + 𝑥 = 195 (các số hạng là các số tự nhiên liên tiếp)

Phương pháp

a) Khi thực hiện cộng (trừ) hỗn số, ta có thể tính nhanh bằng cách cộng (trừ) phần nguyên với phần nguyên, phần thập phân với phần thập phân (Nếu phần thập phân có mẫu số giống nhau)

b) Áp dụng công thức:

Số số hạng của dãy số = (Số hạng cuối – số hạng đầu) : khoảng cách + 1

Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) × số số hạng : 2

Lời giải

a) $8\frac{{14}}{{17}} + (6\frac{3}{{17}} - 5\frac{2}{3})$

= $8\frac{{14}}{{17}} + 6\frac{3}{{17}} - 5\frac{2}{3}$

= $(8\frac{{14}}{{17}} + 6\frac{3}{{17}}) - 5\frac{2}{3}$

= $15 - 5\frac{2}{3}$

= $14\frac{3}{3} - 5\frac{2}{3}$

= $9\frac{1}{3}$ = $\frac{{28}}{3}$

b) 6 + 7 + 8 + 9 + … + 𝑥 = 195

Ta có:

Số số hạng = (x – 6) : 1 + 1 = x – 5

Áp dụng công thức: Tổng của dãy số cách đều = (số hạng đầu + số hạng cuối) × số số hạng : 2

Ta có:

195 = (6 + x) × (x – 5) : 2

(6 + x) × (x – 5) : 2 = 195

(6 + x) × (x – 5)  = 390

x × x + 6 × x – 5 × x – 30 = 390

x × x + (6 – 5) × x – 30 = 390

x × x + x – 30 = 390

x × x + x = 420

x × (x + 1) = 420 (tích của hai số tự nhiên liên tiếp là 420)

Vậy x = 20 (vì 20 × 21 = 420)

Câu 16. Cho hình vuông ABCD. Trên AB lấy điểm M sao cho AM = MB, nối M với D, M với C.

a) Hỏi diện tích hình tam giác DMC gấp mấy lần diện tích hình tam giác DMA?

b) AC cắt MD tại N. Biết diện tích tam giác AND là 5 cm². Tính diện tích hình vuông ABCD.

Phương pháp

a) Tìm mối liên hệ giữa diện tích hình tam giác DMC và diện tích hình tam giác DMA

b) Tìm mối liên hệ giữa diện tích hình tam giác AND và diện tích các hình tam giác khác rồi tính.

Lời giải

a)  Ta có hình vẽ:

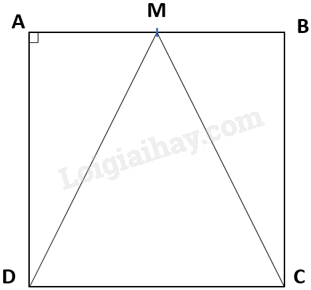
Ta có: AM = MB = $\frac{1}{2}$ AB = $\frac{1}{2}$ DC

Hay DC = 2 × AM

Tam giác DMC có đường cao kẻ từ đỉnh M vuông góc với cạnh DC có độ dài bằng cạnh AD.

Diện tích tam giác DMC là:

$\frac{{AD{\rm{ }} \times {\rm{ }}DC}}{2}$= $\frac{{AD \times {\rm{2}} \times {\rm{AM}}}}{2}$= AD × AM

Diện tích tam giác DMA là:

$\frac{{AD{\rm{ }} \times {\rm{ }}AM}}{2}$

Vậy diện tích tam giác DMC gấp 2 lần diện tích tam giác DMA

b) AC cắt MD tại N.

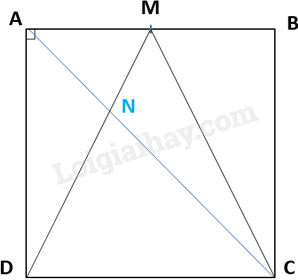
Kẻ đường cao AH từ đỉnh A vuông góc với cạnh MD; đường cao CO từ đỉnh C vuông góc với cạnh MD.

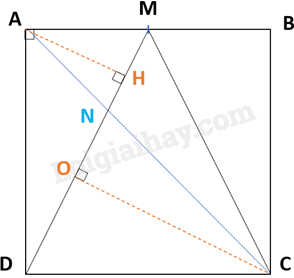
Ta có: CO = 2 AH. (Vì diện tích tam giác DMC = 2 × diện tích tam giác DMA;  tam giác DMC và tam giác DMA có cùng cạnh đáy MD)

Diện tích tam giác DMA = Diện tích tam giác CMA (Vì 2 tam giác này có chiều cao AD = BC và có chung cạnh đáy AM)

Nên diện tích tam giác AND  = Diện tích tam giác CNM = 5 cm² (Vì cùng bằng diện tích tam giác DMA – diện tích tam giác ANM

Diện tích tam giác ANM = Diện tích tam giác CNM : 2 = $\frac{5}{2}$ cm² (Vì 2 tam giác này có chiều cao CO = 2 AH và có chung cạnh đáy MN)

Diện tích tam giác DMA =  Diện tích tam giác ANM + Diện tích tam giác AND  = $\frac{5}{2}$+ 5 = $\frac{{15}}{2}$cm²

Diện tích tam giác DMC là:

$\frac{{15}}{2}$ × 2 = 15 (cm²)

Diện tích tam giác CBM = Diện tích tam giác DMA =  $\frac{{15}}{2}$cm² (Vì 2 tam giác này có chiều cao AD = BC và có cạnh đáy AM = MN)

Diện tích hình vuông ABCD là:

15 + $\frac{{15}}{2}$ + $\frac{{15}}{2}$ = 30 (cm²)

Đáp số: a) 2 lần

          b) 30 cm²