Đề thi vào 10 môn Toán Sóc Trăng năm 2019

Đề bài

Câu 1 (1 điểm):

Rút gọn biểu thức: \(A = \dfrac{{3\sqrt {18}  - 2\sqrt 8 }}{{\sqrt {50} }}.\)

Câu 2 (2 điểm):

Giải phương trình và hệ phương trình:

\(a){\mkern 1mu} {\mkern 1mu} {x^4} - 8{x^2} + 16 = 0;b){\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left\{ {\begin{array}{*{20}{l}}{x + 2y = 4}\\{2x - y = 3}\end{array}} \right.\)

Câu 3 (2 điểm):

Cho hai hàm số \(y = {x^2}\,\,\,\,\left( P \right)\) và \(y =  - x + 2\,\,\,\left( d \right).\)

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phương pháp đại số.

Câu 4 (1,5 điểm):

Năm học 2019 – 2020, bạn An trúng tuyển vào lớp 10 trường THPT X. Để chuẩn bị cho năm học mới, lúc đầu An dự định mua 30 quyển tập và 10 cây viết cùng loại với tổng số tiền phải trả là 340 nghìn đồng. Tuy nhiên, vì đạt danh hiệu học sinh giỏi nên An được nhận phiếu giảm giá 10% với tập và 5% với viết, do đó An quyết định mua 50 quyển tập và 20 cây viết với tổng số tiền phải trả sau giảm giá là 526 nghìn đồng. Hỏi giá tiền mỗi quyển tập và mỗi cây viết là bao nhiêu?

Câu 5 (3 điểm):

Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) trên đường tròn \(\left( O \right)\) lấy điểm \(M\) không trùng với \(A\) hoặc \(B.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) và \(M\) cắt nhau tại điểm \(C.\)

a) Chứng minh tứ giác \(OACM\) nội tiếp.

b) Chứng minh \(MA.MO = MB.MC.\)

c) Gọi \(D\) là giao điểm của \(AC\) và \(BM.\) Chứng minh \(AC = CD.\)

Câu 6 (0,5 điểm):

Bóng đèn huỳnh quang dài 1,2 m  được xem như là một hình trụ với đường kính đáy bằng 4 cm. Tính thể tích khối lượng khí chứa bên trong bóng đèn (độ dày của lớp vỏ thủy tinh xem như không đáng kể).

Lời giải

Câu 1

Phương pháp:

Sử dụng công thức: \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B  = \left\{ \begin{array}{l}A\sqrt B \,\,\,\,khi\,\,\,\,A \ge 0\\ - A\sqrt B \,\,\,\,khi\,\,\,\,A < 0\end{array} \right..\)

Cách giải:

Rút gọn biểu thức: \(A = \dfrac{{3\sqrt {18}  - 2\sqrt 8 }}{{\sqrt {50} }}.\)

\(A = \dfrac{{3\sqrt {18}  - 2\sqrt 8 }}{{\sqrt {50} }} = \dfrac{{3\sqrt {{3^2}.2}  - 2\sqrt {{2^2}.2} }}{{\sqrt {{5^2}.2} }} = \dfrac{{9\sqrt 2  - 4\sqrt 2 }}{{5\sqrt 2 }} = \dfrac{{5\sqrt 2 }}{{5\sqrt 2 }} = 1.\)

Vậy  \(A = 1.\)

Câu 2

Phương pháp:

a) Giải phương trình bằng phương pháp đặt ẩn phụ: \({x^2} = t\,\,\,\left( {t \ge 0} \right).\)

b) Giải hệ phương trình bằng phương pháp thế hoặc phương pháp cộng đại số.

Cách giải:

Giải phương trình và hệ phương trình:

\(a)\,\,{x^4} - 8{x^2} + 16 = 0\)

Đặt \({x^2} = t\,\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình:

\(\begin{array}{l} \Leftrightarrow {t^2} - 8t + 16 = 0 \Leftrightarrow {\left( {t - 4} \right)^2} = 0 \Leftrightarrow t - 4 = 0 \Leftrightarrow t = 4\,\,\left( {tm} \right)\\ \Rightarrow {x^2} = 4 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x =  - 2\end{array} \right..\end{array}\)

Vậy phương trình có tập nghiệm \(S = \left\{ { - 2;\,\,2} \right\}.\)

\(b)\,\,\,\left\{ \begin{array}{l}x + 2y = 4\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x + 4y = 8\\2x - y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 5\\x = 4 - 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 4 - 2.1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right..\)

Vậy hệ phương trình có nghiệm duy nhất: \(\left( {x;\,\,y} \right) = \left( {2;\,\,1} \right).\)

Câu 3

Phương pháp:

a) Lập bảng giá trị và vẽ hai đồ thị hàm số cùng hệ trục tọa độ.

b) Giải phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm. Thế hoành độ giao điểm vừa tìm được vào một trong hai công thức hàm số đã cho để tìm tung độ giao điểm.

Cách giải:

Cho hai hàm số \(y = {x^2}\,\,\,\,\left( P \right)\) và \(y =  - x + 2\,\,\,\left( d \right).\)

a) Vẽ đồ thị \(\left( P \right)\) và \(\left( d \right)\) trên cùng một mặt phẳng tọa độ.

+) Vẽ đồ thị hàm số \(\left( P \right):\,\,\,y = {x^2}\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):\,\,y = {x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\,\,4} \right),\,\,\left( { - 1;\,\,1} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,1} \right),\,\,\,\left( {2;\,\,4} \right)\) và nhận trục \(Oy\) làm trục đối xứng.

+) Vẽ đồ thị hàm số \(\left( d \right):\,\,\,y =  - x + 2\)

Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( d \right):\,\,y =  - x + 2\) là đường thẳng đi qua các điểm \(\left( {0;\,\,2} \right),\,\,\,\left( {2;\,\,0} \right).\)

Đồ thị hàm số:

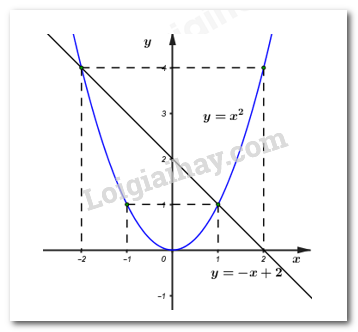
b) Tìm tọa độ giao điểm của hai đồ thị trên bằng phương pháp đại số.

Phương trình hoành độ giao điểm của hai đồ thị hàm số là:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,{x^2} =  - x + 2 \Leftrightarrow {x^2} + x - 2 = 0\\ \Leftrightarrow {x^2} + 2x - x - 2 = 0\\ \Leftrightarrow x\left( {x + 2} \right) - \left( {x + 2} \right) = 0\\ \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = 1\\x =  - 2 \Rightarrow y = {\left( { - 2} \right)^2} = 4\end{array} \right..\end{array}\)

Vậy đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(\left( {1;\,1} \right),\,\,\left( { - 2;\,\,4} \right).\)

Câu 4

Phương pháp:

Giải bài toán bằng cách lập hệ phương trình:

Gọi số tiền 1 quyển tập lúc chưa giảm giá là \(x\) (nghìn đồng) \(\left( {x > 0} \right).\)

Gọi số tiền 1 cây viết lúc chưa giảm giá là \(y\) (nghìn đồng) \(\left( {y > 0} \right).\)

Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết và các ẩn đã gọi.

Lập hệ phương trình, giải hệ phương trình tìm các ẩn, đối chiếu với điều kiện rồi kết luận.

Cách giải:

Gọi số tiền 1 quyển tập lúc chưa giảm giá là \(x\) (nghìn đồng) \(\left( {x > 0} \right).\)

Gọi số tiền 1 cây viết lúc chưa giảm giá là \(y\) (nghìn đồng) \(\left( {y > 0} \right).\)

Lúc đầu, An dự định mua 30 quyển tập và 10 cây viết hết 340 nghìn đồng nên ta có phương trình:

\(30x + 10y = 340\,\,\,\,\,\left( 1 \right).\)

Số tiền mua 1 quyển tập sau khi được giảm giá \(10\% \) là: \(x - x.10\%  = 90\% x\) (nghìn đồng)

Số tiền mua 1 cây viết sau được khi giảm \(5\% \)  là: \(y - y.5\%  = 95\% y\) (nghìn đồng).

An mua 50 quyển tập và 20 cây viết với giá đã được giảm hết 526 nghìn đồng nên ta có phương trình:

\(50.90\% x + 20.95\% y = 526 \Leftrightarrow 45x + 19y = 526\,\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}30x + 10y = 340\\45x + 19y = 526\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + y = 34\\45x + 19y = 526\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}45x + 15y = 510\\45x + 19y = 526\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}4y = 16\\3x + y = 34\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 4\\3x + 4 = 34\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 10\,\,\,\,\left( {tm} \right)\\y = 4\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy giá tiền mỗi quyển tập lúc chưa giảm giá là \(10\) nghìn đồng, mỗi cây viết lúc chưa giảm giá là \(4\) nghìn đồng.

Câu 5

Phương pháp:

a) Sử dụng dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.

b) Chứng minh các tam giác đồng dạng, từ đó suy ra đẳng thức cần chứng minh.

c) Sử dụng tính chất của tiếp tuyến cắt nhau để chứng minh các cạnh bằng nhau.

Cách giải:

Cho đường tròn \(\left( O \right)\) đường kính \(AB,\) trên đường tròn \(\left( O \right)\) lấy điểm \(M\) không trùng với \(A\) hoặc \(B.\) Hai tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\) và \(M\) cắt nhau tại điểm \(C.\)

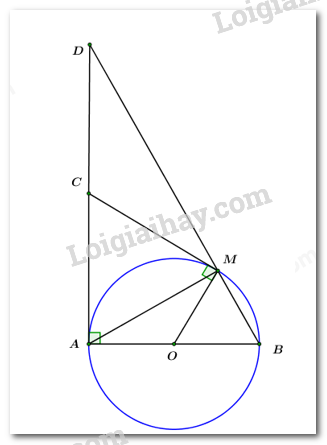
a) Chứng minh tứ giác \(OACM\) nội tiếp.

Ta có: \(CM\) là tiếp tuyến của \(\left( O \right)\) tại\(M \Rightarrow OM \bot MC \Rightarrow \angle OMC = {90^0}.\)

\(AC\) là tiếp tuyến của \(\left( O \right)\) tại \(A \Rightarrow OA \bot CA \Rightarrow \angle OAC = {90^0}.\)

Xét tứ giác \(OACM\) ta có: \(\angle CAO + \angle OMC = {90^0} + {90^0} = {180^0}\)

Mà hai góc này là hai góc đối diện.

\( \Rightarrow OACM\) là tứ giác nội tiếp. (dhnb)

b) Chứng minh \(MA.MO = MB.MC.\)

Ta có: \(\angle AMC = \angle ABM\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(AM\))

Xét \(\Delta OMB\) ta có: \(OM = OB = R \Rightarrow \Delta OMB\) là tam giác cân tại \(O.\)

\( \Rightarrow \angle OMB = \angle OBM.\) (tính chất tam giác cân)

Xét \(\Delta CAM\) ta có: \(CA = CM\) (tính chất hai đường tiếp tuyến cắt nhau).

\( \Rightarrow \Delta CAM\) là tam giác cân tại \(C.\)

\( \Rightarrow \angle CAM = \angle CMA.\) (tính chất tam giác cân)

c) Gọi \(D\) là giao điểm của \(AC\) và \(BM.\) Chứng minh \(AC = CD.\)

Ta có: \(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn \(\left( O \right)\))

\( \Rightarrow AM \bot BM\,\,hay\,\,\,AM \bot BD \Rightarrow \angle AMD = {90^0}\)

\( \Rightarrow \Delta AMD\) là tam giác vuông tại \(M.\)

\( \Rightarrow \left\{ \begin{array}{l}\angle ADM + \angle DAM = {90^0}\\\angle CMA + \angle CMD = {90^0}\end{array} \right.\)

Mà \(\angle CAM = \angle CMA\,\,\,\left( {cm\,\,b} \right)\)

\( \Rightarrow \angle ADM = \angle DMC\,\,\,hay\,\,\,\angle CDM = CMD\)

\( \Rightarrow \Delta CMD\) là tam giác cân tại \(C \Rightarrow CD = CM\)

Mặt khác: \(CA = CM\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow CD = CA\,\,\left( { = CM} \right)\,\,\,\,\left( {dpcm} \right).\)

Câu 6

Phương pháp:

Công thức tính thể tích khối trụ có bán kính đáy \(R\) và chiều cao \(h\) là: \(V = \pi {R^2}h.\)

Cách giải:

Bán kính đát của bóng đèn là: \(4:2 = 2\,\,cm.\)

Chiều cao của bóng đèn là: \(h = 1,2m = 120\,cm.\)

\( \Rightarrow \) Thể tích của lượng khí chứa bên trong bóng đèn là: \(V = \pi {R^2}h = \pi {.2^2}.120 = 480\pi \,\,c{m^3}.\)