Đề thi vào 10 môn Toán Phú Yên năm 2020
I. TRẮC NGHIỆM (3,00 điểm) Câu 1. Rút gọn biểu thức
Đề bài
I. TRẮC NGHIỆM (3,00 điểm)
Câu 1. Rút gọn biểu thức \(M = \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} \), ta được
A. \(M = 1 - \sqrt 2 \) B. \(M = 1 + \sqrt 2 \) C. \(M = \sqrt 2 - 1\) D. \(M = \dfrac{1}{2} - \sqrt 2 \)
Câu 2. Kết quả nào sau đây là sai (với \(a \ge 0,b > 0\))?
A. \(\sqrt a .\sqrt b = \sqrt {ab} \) B. \(\sqrt 9 .\sqrt 3 = 3\sqrt 3 \) C. \(\sqrt 9 + \sqrt 3 = \sqrt {12} \) D. \(\dfrac{{\sqrt a }}{{\sqrt b }} = \sqrt {\dfrac{a}{b}} \)
Câu 3. Biết đồ thị hàm số \(y = ax + 2\) đi qua điểm (–2;4). Khi đó hệ số góc a bằng:
A. –2 B. 4 C. –1 D. 2
Câu 4. Phương trình \(2x - y = 1\) có nghiệm tổng quát là
A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x + 1\end{array} \right.\) B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right.\) C. \(\left( {0; - 1} \right)\) D. \(\left( {1;\,1} \right)\)
Câu 5. Tọa độ các giao điểm của đồ thị hàm số \(\left( P \right):y = {x^2}\) và đường thẳng \(\left( d \right):y = x + 2\) được cho ở hình 1 là
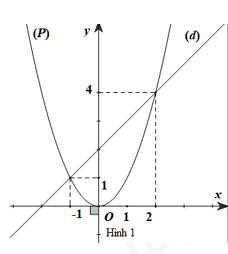
A. (–1;1) và (2;4) B. (–1;1)
C. (2;4) D. (1;–1) và (4;2)
Câu 6. Gọi \({x_1},{x_2}\) là hai nghiệm của phương trình \(2{x^2} - 3x - 5 = 0\). Tính giá trị của biểu thức \(N = {x_1} + {x_2} + {x_1}{x_2}\)
A. \(N = - 1\) B. \(N = - 4\)
C. \(N = - \dfrac{1}{2}\) D. \(N = 2\)
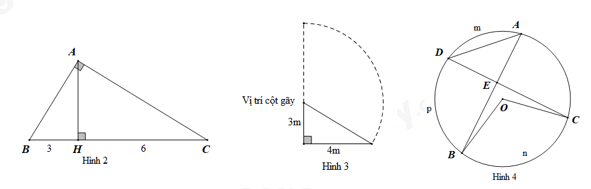
Câu 7. ∆ ABC vuông tại A có đường cao \(AH,BH = 2,HC = 6\) (Hình 2). Độ dài cạnh AB bằng
A. 4 B. \(\sqrt {12} \) C. 12 D. 16
Câu 8. Một trụ điện trồng vuông góc với mặt đất bị bão đánh gãy, ngọn của nó chạm đất và cách gốc 4m, chỗ gãy cách mặt đất 3m (Hình 3). Hỏi khi chưa gãy, trụ điện cao bao nhiêu mét?
A. 4m B. 5m C. 7m D. 8m
Câu 9. Cho hình vẽ như Hình 4. Đẳng thức nào sau đây là sai?

Câu 10. Trên đường tròn đường kính AB lấy các điểm C, D sao cho . Gọi H là giao điểm của AD và BC (Hình 5). Khẳng định nào sau đây là sai?
A.\(AC = CD = DB\) B. \(CH = \dfrac{1}{2}AC\) C. \(\angle AHB = {120^0}\) D. \(\angle ADB = {90^0}\)
Câu 11. Tính diện tích phần tô đậm được tạo bởi nửa đường tròn đường kính OB, đoạn thẳng OA và cung tròn AB, biết \(\angle AOB = {90^0}\) (Hình 6)
A. \(\pi c{m^2}\) B. \(2\pi c{m^2}\) C. \(3\pi c{m^2}\) D. \(4\pi c{m^2}\)
Câu 12. Một chiếc bàn hình tròn, đường kính bằng 1m. Người ta nới rộng mặt bàn bằng cách ghép thêm vào giữa một mặt hình chữ nhật có một cạnh bằng 1m (Hình 7). Để diện tích mặt bàn tăng gấp đôi thì cạnh còn lại của hình chữ nhật đó bằng bao nhiêu mét (cho \(\pi = \dfrac{{22}}{7}\))?
A. \(\dfrac{{11}}{{28}}\) B. \(\dfrac{{22}}{7}\) C. \(\dfrac{{11}}{7}\) D. \(\dfrac{{11}}{{14}}\)
II. TỰ LUẬN (7,00 điểm):
Câu 13. (1,5 điểm) Giải các phương trình, hệ phương trình sau:
a) \(\left\{ \begin{array}{l}x - y = 1\\2x + 3y = 8\end{array} \right.\) b) \(2{x^2} + x - 6 = 0\) c) \({x^4} - 7{x^2} - 8 = 0\)
Câu 14. (2,0 điểm) Cho hàm số \(y = \left( {m - 1} \right)x + 4\) có đồ thị là đường thẳng (d)
a) Xác định m biết đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng –2
b) Vẽ đồ thị hàm số với m vừa tìm được ở câu a
c) Tính khoảng cách từ gốc tọa độ O đến đường thẳng (d)
Câu 15. (1,5 điểm) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Trong một thư viện có hai máy in A và B. Để in 100 trang giấy thì máy A in nhanh hơn máy B là 1 phút. Khi cùng in, thì trong 1 phút cả hai máy in được tổng cộng 45 trang giấy. Tính thời gian để máy A in được 100 trang giấy.
Câu 16. (2,0 điểm) Cho đường tròn \(\left( O \right)\), đường kính \(AB\). Trên \(\left( O \right)\) lấy điểm \(C\) sao cho \(AC < BC\). Trên đoạn thẳng \(OB\) lấy điểm \(I\) cố định (\(I\) khác \(O,B\)). Đường thẳng qua \(I\) vuông góc với \(AB\) cắt \(BC\) tại \(E\), cắt \(AC\) tại \(F\)
a) Chứng minh rằng tứ giác \(ACEI\) là tứ giác nội tiếp.
b) Gọi \(M\) là giao điểm của đường tròn ngoại tiếp tam giác \(AEF\) với \(AB\) (\(M\) khác \(A\)). Chứng minh rằng tam giác \(EBM\) cân.
c) Chứng minh rằng khi C di chuyển trên (O) thì tâm đường tròn ngoại tiếp tam giác AEF chạy trên một đường thẳng cố định.
Lời giải
I. TRẮC NGHIỆM (3,00 điểm)
|
1. C |
2. C |
3. C |
4. B |
5. A |
6. A |
|
7. A |
8. D |
9. D |
10. B |
11. B |
12. D |
Câu 1:
Phương pháp:
Áp dụng công thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\;khi\,A \ge 0\\ - A\;khi\;A < 0\end{array} \right.\)
Cách giải:
Ta có \(M = \sqrt {{{\left( {1 - \sqrt 2 } \right)}^2}} = \left| {1 - \sqrt 2 } \right| = \sqrt 2 - 1\;(do\;\sqrt 2 > 1)\)
Chọn C.
Câu 2:
Phương pháp:
Rút gọn biểu thức chứa dấu căn
Cách giải:
Ta thấy \(\sqrt 9 + \sqrt 3 = 3 + \sqrt 3 ;\sqrt {12} = \sqrt {{2^2}.3} = 2\sqrt 3 \Rightarrow \sqrt 9 + \sqrt 3 \ne \sqrt {12} \)
Chọn C.
Câu 3:
Phương pháp: Thay tọa độ \(\left( { - 2;\,\,4} \right)\) vào hàm số để tìm \(a.\)
Cách giải:
Đồ thị hàm số đi qua điểm \(\left( { - 2;\,\,4} \right)\) nên \(4 = - 2a + 2 \Leftrightarrow 2a = - 2 \Leftrightarrow a = - 1\)
Chọn C.
Câu 4:
Phương pháp:
Cho \(x \in \mathbb{R}\), tính \(y\) theo \(x.\)
Cách giải:
Ta có \(2x - y = 1 \Leftrightarrow y = 2x - 1\)
Nghiệm tổng quát của phương trình đã cho là \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x - 1\end{array} \right.\)
Chọn B.
Câu 5:
Phương pháp:
Quan sát trực tiếp vào đồ thị
Cách giải:
Nhìn vào đồ thị ta thấy hai giao điểm của 2 đồ thị là (–1;1) và (2; 4)
Chọn A.
Câu 6:
Phương pháp:
Áp dụng hệ thức Vi ét và tính giá trị biểu thức
Cách giải:
Áp dụng định lý Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{3}{2}\\{x_1}{x_2} = - \dfrac{5}{2}\end{array} \right.\)\( \Rightarrow N = {x_1} + {x_2} + {x_1}{x_2} = \dfrac{3}{2} - \dfrac{5}{2} = - 1\)
Chọn A.
Câu 7:
Phương pháp:
Áp dụng hệ thức lượng trong tam giác vuông
Cách giải::
Áp dụng hệ thức lượng trong tam giác vuông ta có:
\(A{B^2} = BH.BC = 2.\left( {2 + 6} \right) = 16 \Rightarrow AB = 4\)
Chọn A.
Câu 8:
Phương pháp:
Áp dụng định lý Pitago
Cách giải:
Áp dụng định lý Pitago, ta có đoạn cột điện từ chỗ gãy đến ngọn có độ dài là \(\sqrt {{3^2} + {4^2}} = 5\left( m \right)\)
Độ dài của cả cột điện là: \(3 + 5 = 8\,\,\left( m \right).\)
Chọn D.
Câu 9:
Phương pháp:
Áp dụng công thức góc nội tiếp, góc ngoài tam giác
Cách giải:
Vì góc BEC là góc ngoài tam giác AEC nên: \(\angle BEC = \angle BAC + \angle ACE\)\( = \dfrac{1}{2}\angle BOC + \angle ACE > \dfrac{1}{2}\angle BOC\)
Khẳng định D là sai
Chọn D.
Câu 10:
Phương pháp:
Tính số đo các góc, từ đó giải tam giác ACH
Cách giải:
Ta có:
\( \Rightarrow \angle CAH = {30^0}\)
Mặt khác tam giác ACH vuông do \(\angle ACH = {90^0}\) (góc nội tiếp chắn nửa đường tròn) nên \(\dfrac{{CH}}{{AC}} = \tan {30^0} = \dfrac{1}{{\sqrt 3 }}\)
Chọn B.
Câu 11:
Phương pháp:
Diện tích phần tô đậm là hiệu của diện tích cung tròn OAB với diện tích nửa đường tròn đường kính OB
Cách giải:
Diện tích phần tô đậm là \(\dfrac{1}{4}\pi {.4^2} - \dfrac{1}{2}\pi {.2^2} = 2\pi \left( {c{m^2}} \right)\)
Chọn B.
Câu 12 Diện tích hình tròn
Phương pháp:
Để diện tích mặt bàn tăng gấp đôi thì diện tích hình chữ nhật phải bằng diện tích hình tròn ban đầu.
Cách giải:
Diện tích chiếc bàn tròn ban đầu là \(\pi .{\left( {\dfrac{1}{2}} \right)^2} = \dfrac{\pi }{4}\left( {{m^2}} \right)\)
Chiều dài hình chữ nhật phải tăng thêm là \(\dfrac{{\dfrac{\pi }{4}}}{1} = \dfrac{{11}}{{14}}\left( m \right)\)
Chọn D.
II. TỰ LUẬN (7,00 điểm)
Câu 13. (1,50 điểm)
Cách giải:
Giải các phương trình, hệ phương trình sau:
a) \(\left\{ \begin{array}{l}x - y = - 1\\2x + 3y = 8\end{array} \right.\)
Ta có:
\(\left\{ \begin{array}{l}x - y = - 1\\2x + 3y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2x - 2y = - 2\\2x + 3y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5y = 10\\x = y - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 2 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 1\end{array} \right.\).
Vậy hệ phương trình có nghiệm duy nhất \(\left( {x;y} \right) = \left( {1;2} \right)\).
b) \(2{x^2} + x - 6 = 0\)
Ta có: \(\Delta = {1^2} - 4.2.\left( { - 6} \right) = 1 + 48 = 49 > 0\).
Do đó phương trình có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 1 + \sqrt {49} }}{{2.2}} = \dfrac{3}{2}\\{x_2} = \dfrac{{ - 1 - \sqrt {49} }}{{2.2}} = - 2\end{array} \right.\).
Vậy tập nghiệm của phương trình là \(S = \left\{ {\dfrac{3}{2}; - 2} \right\}\).
c) \({x^4} - 7{x^2} - 8 = 0\).
Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), phương trình đã cho trở thành: \({t^2} - 7t - 8 = 0\,\,\left( * \right)\).
Nhận xét: \(a - b + c = 1 - \left( { - 7} \right) - 8 = 0\) nên phương trình (*) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{t_1} = - 1\,\,\,\,\,\,\,\,\,\,\,\,\left( {ktm} \right)\\{t_2} = - \dfrac{c}{a} = 8\,\,\left( {tm} \right)\end{array} \right.\) .
Với \(t = 8 \Rightarrow {x^2} = 8 \Leftrightarrow x = \pm 2\sqrt 2 \).
Vậy tập nghiệm của phương trình là \(S = \left\{ { \pm 2\sqrt 2 } \right\}\).
Câu 14. (2,00 điểm)
Cách giải:
Cho hàm số \(y = \left( {m - 1} \right)x + 4\) có đồ thị là đường thẳng \(\left( d \right)\).
a) Xác định m biết đường thẳng \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 2\).
Vì đường thẳng \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 2\) nên đường thẳng \(\left( d \right)\) đi qua điểm có tọa độ \(\left( { - 2;0} \right)\).
\(\begin{array}{l} \Rightarrow 0 = \left( {m - 1} \right).\left( { - 2} \right) + 4\\ \Leftrightarrow 2\left( {m - 1} \right) = 4\\ \Leftrightarrow m - 1 = 2\\ \Leftrightarrow m = 3\end{array}\)
Vậy \(m = 3\).
b) Vẽ đồ thị hàm số với \(m\) vừa thu được ở câu a.
Theo câu a) ta có \(m = 3\), khi đó hàm số trở thành \(y = 2x + 4\).
Ta có bảng giá trị sau:
|
\(x\) |
\(0\) |
\( - 2\) |
|
\(y\) |
\(4\) |
\(0\) |
Do đó đồ thị hàm số \(y = 2x + 4\) là đường thẳng đi qua hai điểm có tọa độ \(A\left( { - 2;0} \right)\) và \(B\left( {0;4} \right)\).
Đồ thị hàm số:
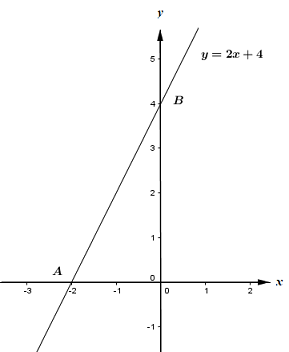
c) Tính khoảng cách từ gốc tọa độ \(O\) đến đường thẳng \(\left( d \right)\).
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 2x + 4\) cắt trục hoành tại điểm \(A\left( { - 2;0} \right)\) và cắt trục tung tại điểm \(B\left( {0;4} \right)\).
\( \Rightarrow OA = \left| { - 2} \right| = 2,\,\,\,OB = \left| 4 \right| = 4\).
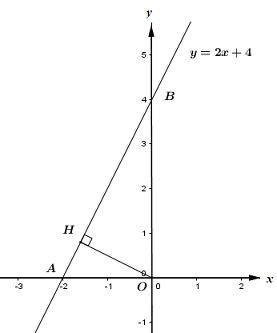
Kẻ \(OH \bot d\,\,\left( {H \in AB} \right)\).
Áp dụng hệ thức lượng trong tam giác \(OAB\) vuông tại \(O\), đường cao \(OH\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}}\\ \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{{2^2}}} + \dfrac{1}{{{4^2}}}\\ \Leftrightarrow \dfrac{1}{{O{H^2}}} = \dfrac{5}{{16}}\\ \Rightarrow O{H^2} = \dfrac{{16}}{5}\\ \Rightarrow OH = \sqrt {\dfrac{{16}}{5}} = \dfrac{{4\sqrt 5 }}{5}\end{array}\)
Vậy khoảng cách từ gốc tọa độ O đến đường thẳng \(\left( d \right)\) bằng \(OH\) và bằng \(\dfrac{{4\sqrt 5 }}{5}\).
Câu 15. (1,50 điểm)
Cách giải:
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình
Trong một thư viện có hai máy in A và B. Để in 100 trang giấy thì máy A in nhanh hơn máy B là 1 phút. Khi cùng in, thì trong 1 phút cả hai máy in được tổng cộng 45 trang giấy. Tính thời gian để máy A in được 100 trang giấy.
Gọi thời gian máy A in được 100 trang giấy là \(x\) (phút) (ĐK: \(x > 0\)).
\( \Rightarrow \) Thời gian máy B in được 100 trang giấy là \(x + 1\) (phút).
Khi cùng in, trong 1 phút:
Máy A in được: \(\dfrac{{100}}{x}\) (trang giấy)
Máy B in được: \(\dfrac{{100}}{{x + 1}}\) (trang giấy)
\( \Rightarrow \) Trong 1 phút, cả hai máy in được \(\dfrac{{100}}{x} + \dfrac{{100}}{{x + 1}}\) (trang giấy)
Vì trong 1 phút, cả hai máy in được tổng cộng 45 trang giấy nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{100}}{x} + \dfrac{{100}}{{x + 1}} = 45\\ \Leftrightarrow \dfrac{{20}}{x} + \dfrac{{20}}{{x + 1}} = 9\\ \Leftrightarrow 20\left( {x + 1} \right) + 20x = 9x\left( {x + 1} \right)\\ \Leftrightarrow 20x + 20 + 20x = 9{x^2} + 9x\\ \Leftrightarrow 9{x^2} - 31x - 20 = 0\\ \Leftrightarrow 9{x^2} - 36x + 5x - 20 = 0\\ \Leftrightarrow 9x\left( {x - 4} \right) + 5\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 4} \right)\left( {9x + 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 4 = 0\\9x + 5 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 4\,\,\,\,\,\,\,\left( {tm} \right)\\x = - \dfrac{5}{9}\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy thời gian để máy A in được 100 trang giấy là 4 phút.
Câu 16. (2,00 điểm)
Cách giải:
Cho đường tròn \(\left( O \right)\), đường kính \(AB\). Trên \(\left( O \right)\) lấy điểm \(C\) sao cho \(AC < BC\). Trên đoạn thẳng \(OB\) lấy điểm \(I\) cố định (\(I\) khác \(O,B\)). Đường thẳng qua \(I\) vuông góc với \(AB\) cắt \(BC\) tại \(E\), cắt \(AC\) tại \(F\).
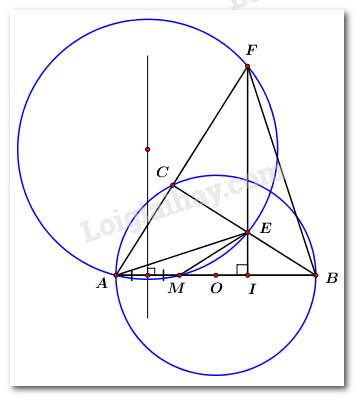
a) Chứng minh rằng tứ giác \(ACEI\) là tứ giác nội tiếp.
Vì \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn nên \(\angle ACB = {90^0} \Rightarrow \angle ACE = {90^0}\).
Xét tứ giác \(ACEI\) có: \(\angle ACE + \angle AIE = {90^0} + {90^0} = {180^0}\).
\( \Rightarrow \) Tứ giác \(ACEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng \({180^0}\)).
b) Gọi \(M\) là giao điểm của đường tròn ngoại tiếp tam giác \(AEF\) với \(AB\) (\(M\) khác \(A\)). Chứng minh rằng tam giác \(EBM\) cân.
Vì tứ giác \(AMEF\) là tứ giác nội tiếp (các điểm \(A,\,\,M,\,\,E,\,\,F\) cùng thuộc đường tròn ngoại tiếp \(\Delta AEF\)) nên \(\angle EMI = \angle AFE = \angle AFI\,\,\left( 1 \right)\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Ta lại có:
\(\angle AFI + \angle FAI = {90^0}\) (do tam giác \(AFI\) vuông tại \(I\)).
\(\angle ABC + \angle CAB = {90^0} \Rightarrow \angle ABC + \angle FAI = {90^0}\) (do tam giác \(ABC\) vuông tại \(C\)).
\( \Rightarrow \angle AFI = \angle ABC\) (cùng phụ với \(\angle FAI\)).
\( \Rightarrow \angle AFI = \angle EBI\,\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow \angle EMI = \angle EBI\,\,\left( { = \angle AFI} \right)\).
\( \Rightarrow \Delta EBM\) cân tại \(E\) (định nghĩa) (đpcm).
c) Chứng minh rằng khi C di chuyển trên (O) thì tâm đường tròn ngoại tiếp tam giác AEF chạy trên một đường thẳng cố định.
Ta có: \(\Delta EBM\) cân tại \(E\) (cmt), mà \(EI \bot BM\) nên \(I\) là trung điểm của \(BM\) (đường cao đồng thời là trung tuyến) \( \Rightarrow M\) là điểm đối xứng với \(B\) qua \(I\) và \(IB = IM\).
Mà \(I,\,\,A,\,\,B\) cố định \( \Rightarrow IB\) không đổi \( \Rightarrow IM\) không đổi.
Lại có \(I\) cố định \( \Rightarrow M\) cố định.
Đường tròn ngoại tiếp tam giác \(AEF\) đi qua điểm \(M\), nên tâm đường tròn ngoại tiếp tam giác \(AEF\) thuộc đường trung trực của \(AM\).
Vì \(A,\,\,M\) cố định nên trung trực của \(AM\) là cố định.
Vậy tâm đường tròn ngoại tiếp tam giác \(AEF\) thuộc trung trực của \(AM\) cố định, với \(M\) là điểm đối xứng với \(B\) qua \(I\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Phú Yên năm 2020 timdapan.com"







