Đề thi vào 10 môn Toán Ninh Bình năm 2023

Câu 1: 1. Rút gọn biểu thức $A = 3\sqrt {16} {\rm{ \;}} - 2\sqrt 9 {\rm{ \;}} + \sqrt 4 $ 2. Tìm giá trị của tham số m để đường thẳng $\left( {{d_1}} \right):y = \left( {m - 1} \right)x - 2$ song song với đường thẳng $\left( {{d_2}} \right):y = 2x + 3$. 3. Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 10}\\{x - 2y = 1}\end{array}} \right.$

Đề bài

Câu 1:

1. Rút gọn biểu thức $A = 3\sqrt {16} {\rm{ \;}} - 2\sqrt 9 {\rm{ \;}} + \sqrt 4 $

2. Tìm giá trị của tham số m để đường thẳng $\left( {{d_1}} \right):y = \left( {m - 1} \right)x - 2$ song song với đường thẳng $\left( {{d_2}} \right):y = 2x + 3$.

3. Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 10}\\{x - 2y = 1}\end{array}} \right.$

Câu 2:

1. Rút gọn biểu thức $B = \frac{{x\sqrt x {\rm{ \;}} - 1}}{{x - 1}} - \frac{x}{{\sqrt x {\rm{ \;}} + 1}} + \frac{1}{{\sqrt x {\rm{ \;}} - 1}}$ với $x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1$.

2. Cho phương trình ${x^2} - 2mx + 4m - 4 = 0{\mkern 1mu} {\mkern 1mu} \left( 1 \right)$ (x là ẩn số, m là tham số)

a) Giải phương trình (1) với m = 3.

b) Tìm tất cả các giá trị của m để phương trình (1) có 2 nghiệm phân biệt ${x_1},{\mkern 1mu} {\mkern 1mu} {x_2}$ thoả mãn $\sqrt {{x_1}} {\rm{ \;}} + \sqrt {{x_2}} {\rm{ \;}} = 3\sqrt 2 $

Câu 3: Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Hai đội công nhân làm chung một công việc thì làm xong trong 12 ngày. Khi làm riêng, để hoàn thành công việc trên thì đội thứ nhất cần nhiều thời gian hơn đội thứ hai là 10 ngày. Hỏi nếu làm riêng thì trong bao nhiêu ngày mỗi đội sẽ làm xong công việc trên?

Câu 4:

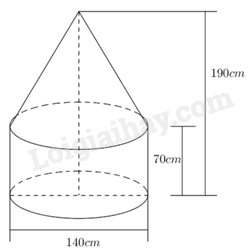
1. Một dụng cụ gồm hai phần: một phần có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước cho như hình vẽ bên.

a) Tính chiều cao của dụng cụ hình nón.

b) Tính thể tích dụng cụ đã cho (lấy $\pi {\rm{ \;}} = 3,14$ ).

2. Cho đường tròn tâm O, đường kính AB. Lấy điểm H nằm giữa O và B $(H \ne O;H \ne B)$, vẽ dây cung MN của đường tròn (O) vuông góc với AB tại H. Trên đường thẳng MN lấy điểm C nằm ngoài đường tròn (O) sao cho $CM > CN$. Đoạn thẳng AC cắt đường tròn (O) tại điểm $K{\mkern 1mu} {\mkern 1mu} \left( {K \ne A} \right)$. Hai dây cung MN và BK cắt nhau tại E.

a) Chứng minh tứ giác AHEK là tứ giác nội tiếp.

b) Chứng minh CM.CN = CK.CA.

c) Từ điểm N vẽ đường thẳng vuông góc với đường thẳng AC, đường thẳng này cắt tia MK tại F. Chứng minh tam giác KFN là tam giác cân.

Câu 5:

1. Tìm tất cả các cặp số nguyên (x;y) thoả mãn $2{x^2} - x{y^2} - 2x + {y^2} + 5 = 0$.

2. Biết a, b, c là ba số thực dương thoả mãn điều kiện: $\sqrt a {\rm{ \;}} + \sqrt b {\rm{ \;}} + \sqrt c {\rm{ \;}} = 3$.

Chứng minh $\sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} + \sqrt {2{b^2} + 3bc + 2{c^2}} {\rm{ \;}} + \sqrt {2{c^2} + 3ca + 2{a^2}} {\rm{ \;}} \ge 3\sqrt 7 $.

----- HẾT -----

Lời giải chi tiết

Câu 1 (TH):

Phương pháp:

1) Khai phương căn bậc hai và rút gọn

2) $d\parallel d' \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = a'}\\{b \ne b'}\end{array}} \right.$

3) Giải hệ bằng phương pháp cộng đại số

Cách giải:

1. Rút gọn biểu thức $A = 3\sqrt {16} {\rm{ \;}} - 2\sqrt 9 {\rm{ \;}} + \sqrt 4 $

$\begin{array}{*{20}{l}}{A = 3\sqrt {16} {\rm{ \;}} - 2\sqrt 9 {\rm{ \;}} + \sqrt 4 }\\{A = 3\sqrt {{4^2}} {\rm{ \;}} - 2\sqrt {{3^2}} {\rm{ \;}} + \sqrt {{2^2}} }\\{A = 3.4 - 2.3 + 2}\\{A = 12 - 6 + 2}\\{A = 6 + 2}\\{A = 8}\end{array}$

Vậy $A = 8.$

2. Tìm giá trị của tham số m để đường thẳng $\left( {{d_1}} \right):y = \left( {m - 1} \right)x - 2$ song song với đường thẳng $\left( {{d_2}} \right):y = 2x + 3$.

Hai đường thẳng $\left( {{d_1}} \right)$và $\left( {{d_2}} \right)$ song song với nhau khi và chỉ khi $\left\{ {\begin{array}{*{20}{l}}{m - 1 = 2}\\{ - 2 \ne 3{\mkern 1mu} {\mkern 1mu} \left( {luon{\mkern 1mu} {\mkern 1mu} dung} \right)}\end{array}} \right. \Leftrightarrow m = 3$

Vậy $m = 3$.

3. Giải hệ phương trình $\left\{ {\begin{array}{*{20}{l}}{3x + y = 10}\\{x - 2y = 1}\end{array}} \right.$

Ta có: $\left\{ {\begin{array}{*{20}{l}}{3x + y = 10}\\{x - 2y = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{3x + y = 10}\\{3x - 6y = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{7y = 7}\\{x = 2y + 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{y = 1}\\{x = 3}\end{array}} \right.$.

Vậy hệ phương trình có nghiệm duy nhất là: $\left( {x;y} \right) = \left( {3;1} \right).$

Câu 2 (VD):

Phương pháp:

1) Phân tích mẫu số tìm mẫu số chung, quy đồng và rút gọn biểu thức

2a) Thay m = 3 và giải phương trình bậc hai

2b) Áp dụng hệ thức viet.

Cách giải:

Với $x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1$ ta có:

$\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B = \frac{{x\sqrt x - 1}}{{x - 1}} - \frac{x}{{\sqrt x + 1}} + \frac{1}{{\sqrt x - 1}}}\\{ \Leftrightarrow B = \frac{{x\sqrt x - 1 - x\left( {\sqrt x - 1} \right) + \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{ \Leftrightarrow B = \frac{{x\sqrt x - 1 - x\sqrt x + x + \sqrt x + 1}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{ \Leftrightarrow B = \frac{{x + \sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{ \Leftrightarrow B = \frac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}}\\{ \Leftrightarrow B = \frac{{\sqrt x }}{{\sqrt x - 1}}}\end{array}$

Vậy với $x \ge 0,{\mkern 1mu} {\mkern 1mu} x \ne 1$ thì $B = \frac{{\sqrt x }}{{\sqrt x {\rm{ \;}} - 1}}$.

2. Cho phương trình ${x^2} - 2mx + 4m - 4 = 0{\mkern 1mu} {\mkern 1mu} \left( 1 \right)$ (x là ẩn số, m là tham số)

a) Giải phương trình (1) với m = 3.

Thay m = 3 vào phương trình (1) ta được: ${x^2} - 6x + 8 = 0$.

Ta có: $\Delta ' = {\left( { - 3} \right)^2} - 1.8 = 1 > 0$ nên phương trình có 2 nghiệm phân biệt: $\left[ {\begin{array}{*{20}{l}}{{x_1} = 3 + 1 = 4}\\{{x_2} = 3 - 1 = 2}\end{array}} \right.$.

Vậy khi m = 3 thì tập nghiệm của phương trình (1) là $S = \left\{ {2;4} \right\}$.

Để phương trình (1) có 2 nghiệm phân biệt ${x_1},{\mkern 1mu} {\mkern 1mu} {x_2}$ thoả mãn $\sqrt {{x_1}} {\rm{ \;}} + \sqrt {{x_2}} {\rm{ \;}} = 3\sqrt 2 $ thì

$\left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{x_1} \ge 0}\\{{x_2} \ge 0}\\{\sqrt {{x_1}} + \sqrt {{x_2}} = 3\sqrt 2 }\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{m^2} - 4m + 4 > 0}\\{{x_1} + {x_2} \ge 0}\\{{x_1}{x_2} \ge 0}\\{{{\left( {\sqrt {{x_1}} + \sqrt {{x_2}} } \right)}^2} = 18}\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{\left( {m - 2} \right)}^2} > 0}\\{2m \ge 0}\\{4m - 4 \ge 0}\\{{x_1} + {x_2} + 2\sqrt {{x_1}{x_2}} = 18}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m - 2 \ne 0}\\{m \ge 0}\\{m \ge 1}\\{2m + 2\sqrt {4m - 4} = 18}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m \ge 1,{\mkern 1mu} {\mkern 1mu} m \ne 2}\\{m + 2\sqrt {m - 1} = 9{\mkern 1mu} {\mkern 1mu} \left( * \right)}\end{array}} \right.} \right.$

Đặt $t = \sqrt {m - 1} {\mkern 1mu} {\mkern 1mu} \left( {t \ge 0,{\mkern 1mu} {\mkern 1mu} t \ne 1} \right)$ $ \Rightarrow {t^2} = m - 1 \Leftrightarrow m = {t^2} + 1$

Khi đó phương trình (*) trở thành ${t^2} + 1 + 2t = 9 \Leftrightarrow {t^2} + 2t - 8 = 0$.

Ta có $\Delta {'_t} = {1^2} - \left( { - 8} \right) = 9 > 0$ nên phương trình (*) có 2 nghiệm phân biệt

$\left[ {\begin{array}{*{20}{l}}{{t_1} = {\rm{ \;}} - 1 + 3 = 2{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\\{{t_1} = {\rm{ \;}} - 1 - 3 = {\rm{ \;}} - 4{\mkern 1mu} \left( {Ktm} \right)}\end{array}} \right.$

Với $t = 2 \Rightarrow \sqrt {m - 1} {\rm{ \;}} = 2 \Leftrightarrow m - 1 = 4 \Leftrightarrow m = 5{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)$.

Vậy m = 5.

Câu 3 (VD):

Phương pháp:

Gọi thời gian để đội thứ nhất làm riêng xong công việc là $x$ (ngày, $x \in \mathbb{N},x > 12$)

Biểu diễn thời gian mỗi ngày từng đội làm được theo x, lập phương trình tìm x.

Cách giải:

Gọi thời gian để đội thứ nhất làm riêng xong công việc là $x$ (ngày, $x \in \mathbb{N},x > 12$)

Khi làm riêng, để hoàn thành công việc trên thì đội thứ nhất cần nhiều thời gian hơn đội thứ hai là 10 ngày nên thời gian để đội thứ hai làm riêng xong công việc là $x - 10$ (ngày)

Mỗi ngày đội thứ nhất làm được: $\frac{1}{x}$ (công việc)

Mỗi ngày đội thứ hai làm được: $\frac{1}{{x - 10}}$ (công việc)

Mỗi ngày cả hai đội làm được $\frac{1}{{12}}$ (công việc)

Khi đó ta có phương trình: $\frac{1}{x} + \frac{1}{{x - 10}} = \frac{1}{{12}}$

$\begin{array}{*{20}{l}}{ \Leftrightarrow \frac{{12\left( {x - 10} \right)}}{{12x\left( {x - 10} \right)}} + \frac{{12x}}{{12x\left( {x - 10} \right)}} = \frac{{x\left( {x - 10} \right)}}{{12x\left( {x - 10} \right)}}}\\{ \Rightarrow 12\left( {x - 10} \right) + 12x = x\left( {x - 10} \right)}\\{ \Leftrightarrow 12x - 120 + 12x = {x^2} - 10x}\\{ \Leftrightarrow {x^2} - 34x + 120 = 0}\\{ \Leftrightarrow {x^2} - 30x - 4x + 120 = 0}\\{ \Leftrightarrow x\left( {x - 30} \right) - 4\left( {x - 30} \right) = 0}\\{ \Leftrightarrow \left( {x - 30} \right)\left( {x - 4} \right) = 0}\\{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x - 30 = 0}\\{x - 4 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 30{\mkern 1mu} {\mkern 1mu} ({\rm{TM}})}\\{x = 4{\mkern 1mu} {\mkern 1mu} ({\rm{KTM}})}\end{array}} \right.}\end{array}$

Vậy đội thứ nhất làm xong công việc trong 30 ngày, đội thứ hai làm xong công việc là 20 ngày.

Câu 4 (VD):

Phương pháp:

1. Áp dụng công thức tính thể tích hình nón, hình trụ

2. a) Tổng hai góc đối diện bằng ${180^0}$

b) Chứng minh $\Delta CKN$ và $\Delta CMA$ đồng dạng

c) Chứng minh $\angle NFK = \angle NKF$ từ đó suy ra tam giác cân.

Cách giải:

1. Một dụng cụ gồm hai phần: một phần có dạng hình trụ, phần còn lại có dạng hình nón với các kích thước cho như hình vẽ bên.

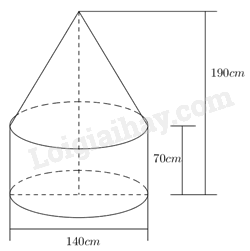
Chiều cao của phần dụng cụ có dạng hình nón là: $190 - 70 = 120{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {cm} \right).$

b) Tính thể tích dụng cụ đã cho (lấy $\pi {\rm{ \;}} = 3,14$ ).

Ta thấy đáy hình trụ có đường kính bằng 140cm nên bán kính $r = 70{\mkern 1mu} {\mkern 1mu} \left( {cm} \right)$.

Thể tích phần dụng cụ có dạng hình nón là:

${V_1} = \frac{1}{3}\pi .{r^2}.{h_1} = \frac{1}{3}.3,{14.70^2}.120 = 615{\mkern 1mu} {\mkern 1mu} 440{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)$.

Thể tích phần dụng cụ có dạng hình trụ là:

${V_2} = \pi .{r^2}.{h_2} = 3,{14.70^2}.70 = 1{\mkern 1mu} {\mkern 1mu} 077{\mkern 1mu} {\mkern 1mu} 020{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {c{m^3}} \right)$.

Thể tích dụng cụ đã cho là:

$V = {V_1} + {V_2} = 615{\mkern 1mu} {\mkern 1mu} 440{\mkern 1mu} + {\mkern 1mu} 1{\mkern 1mu} {\mkern 1mu} 077{\mkern 1mu} {\mkern 1mu} 020 = 1{\mkern 1mu} 692{\mkern 1mu} 460\left( {c{m^3}} \right)$.

2. Cho đường tròn tâm O, đường kính AB. Lấy điểm H nằm giữa O và B $(H \ne O;H \ne B)$, vẽ dây cung MN của đường tròn (O) vuông góc với AB tại H. Trên đường thẳng MN lấy điểm C nằm ngoài đường tròn (O) sao cho CM > CN. Đoạn thẳng AC cắt đường tròn (O) tại điểm $K{\mkern 1mu} {\mkern 1mu} \left( {K \ne A} \right)$. Hai dây cung MN và BK cắt nhau tại E.

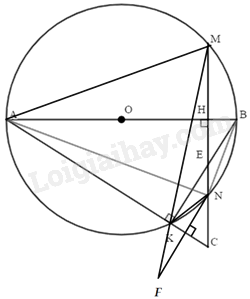
Ta có:

$\angle AKE = \angle AKB = {90^0}$ (góc nội tiếp chắn nửa đường tròn)

$\angle AHE = {90^0}$ (do $MN \bot AB$ tại H)

Xét tứ giác AHEK có: $\angle AKE + \angle HE = {90^0} + {90^0} = {180^0}$

Suy ra tứ giác AKEH nội tiếp đường tròn. (tứ giác có tổng hai góc đối bằng ${180^0}$)

b) Chứng minh CM.CN = CK.CA.

Vì AKNM nội tiếp đường tròn (O) $ \Rightarrow \angle CNK = \angle CAM$ (góc ngoài và góc trong tại đỉnh đối diện).

Xét $\Delta CKN$ và $\Delta CMA$ có:

$\begin{array}{*{35}{l}} \angle ACMchung \\ \angle CNK=\angle CAM\left( cmt \right) \\ \Rightarrow \Delta CKN\backsim \Delta CMA\left( g.g \right) \\\end{array}$

$ \Rightarrow \frac{{CK}}{{CM}} = \frac{{CN}}{{CA}} \Rightarrow CM.CN = CK.CA$ (đpcm) (cặp cạnh tương ứng tỉ lệ).

c) Từ điểm N vẽ đường thẳng vuông góc với đường thẳng AC, đường thẳng này cắt tia MK tại F. Chứng minh tam giác KFN là tam giác cân.

Do $NF \bot AC\left( {gt} \right),BK \bot AC$ (do $\angle BKA = {90^0}$, góc nội tiếp chắn nửa đường tròn)

$ \Rightarrow FN\parallel BK$ (từ vuông góc đến song song).

$ \Rightarrow \angle KNF = \angle BKN$ (hai góc so le trong bằng nhau) và $\angle NFK = \angle BKM$ (hai góc đồng vị bằng nhau)

Do $OB \bot MN$ tại H (giả thiết) nên H là trung điểm MN (tính chất đường kính vuông góc với dây cung)

Xét tam giác OMN có OH vừa là đường cao vừa là trung tuyến nên tam giác OMN cân tại O

=> OH đồng thời là phân giác

(góc nội tiếp)

$ \Rightarrow \angle NKB = \angle BKM$ (hai góc nội tiếp chắn 2 cung bằng nhau)

$ \Rightarrow NFK = \angle NKF$

$ \Rightarrow \Delta KNF$ cân tại K (định nghĩa) (đpcm).

Câu 5 (VDC):

Phương pháp:

1. Phân tích biểu thức về dạng $f\left( x \right).g\left( x \right) = m$

2. Chứng minh $\sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} = \sqrt {\frac{7}{4}{{\left( {a + b} \right)}^2} + \frac{1}{4}{{\left( {a - b} \right)}^2}} {\rm{ \;}} \ge \frac{{\sqrt 7 }}{2}\left( {a + b} \right)$

Cách giải:

1. Tìm tất cả các cặp số nguyên (x;y) thoả mãn $2{x^2} - x{y^2} - 2x + {y^2} + 5 = 0$.

Ta có:

$\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 2{x^2} - x{y^2} - 2x + {y^2} + 5 = 0}\\{ \Leftrightarrow \left( {2{x^2} - 2x} \right) - \left( {x{y^2} - {y^2}} \right) = {\rm{ \;}} - 5}\\{ \Leftrightarrow 2x\left( {x - 1} \right) - {y^2}\left( {x - 1} \right) = {\rm{ \;}} - 5}\\{ \Leftrightarrow \left( {x - 1} \right)\left( {2x - {y^2}} \right) = {\rm{ \;}} - 5}\end{array}$

Vì $x,{\mkern 1mu} {\mkern 1mu} y$ là số nguyên nên $x - 1$ và $2x - {y^2}$ cũng là số nguyên

Do đó $\left( {x - 1} \right)\left( {2x - {y^2}} \right) = {\rm{ \;}} - 5$ ta xét các trường hợp sau:

TH1: $\left\{ {\begin{array}{*{20}{l}}{x - 1 = 5}\\{2x - {y^2} = {\rm{ \;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{12 - {y^2} = {\rm{ \;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{{y^2} = 13{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.$.

TH2: $\left\{ {\begin{array}{*{20}{l}}{x - 1 = {\rm{ \;}} - 5}\\{2x - {y^2} = 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 4}\\{ - 8 - {y^2} = {\rm{ \;}} - 1}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {\rm{ \;}} - 4}\\{{y^2} = {\rm{ \;}} - 7{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.$.

TH3: $\left\{ {\begin{array}{*{20}{l}}{x - 1 = 1}\\{2x - {y^2} = {\rm{ \;}} - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{4 - {y^2} = {\rm{ \;}} - 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{{y^2} = 9 \Leftrightarrow y = {\rm{ \;}} \pm 3{\mkern 1mu} {\mkern 1mu} \left( {tm} \right)}\end{array}} \right.$

TH4: $\left\{ {\begin{array}{*{20}{l}}{x - 1 = {\rm{ \;}} - 1}\\{2x - {y^2} = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 0}\\{{y^2} = {\rm{ \;}} - 5{\mkern 1mu} {\mkern 1mu} \left( {ktm} \right)}\end{array}} \right.$.

Vậy có 2 cặp số nguyên (x;y) thoả mãn là (2;3) và (2;-3).

2. Biết a, b, c là ba số thực dương thoả mãn điều kiện: $\sqrt a {\rm{ \;}} + \sqrt b {\rm{ \;}} + \sqrt c {\rm{ \;}} = 3$.

Chứng minh $\sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} + \sqrt {2{b^2} + 3bc + 2{c^2}} {\rm{ \;}} + \sqrt {2{c^2} + 3ca + 2{a^2}} {\rm{ \;}} \ge 3\sqrt 7 $.

Ta có:

$\sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} = \sqrt {\frac{7}{4}{{\left( {a + b} \right)}^2} + \frac{1}{4}{{\left( {a - b} \right)}^2}} {\rm{ \;}} \ge \frac{{\sqrt 7 }}{2}\left( {a + b} \right)$

Tuơng tự ta có:

$\begin{array}{*{20}{l}}{\sqrt {2{b^2} + 3bc + 2{c^2}} {\rm{ \;}} \ge \frac{{\sqrt 7 }}{2}\left( {b + c} \right)}\\{\sqrt {2{c^2} + 3ca + 2{a^2}} {\rm{ \;}} \ge \frac{{\sqrt 7 }}{2}\left( {c + a} \right)}\end{array}$

Cộng vế theo vế 3 bất phương trình ta được:

$\begin{array}{*{20}{l}}{\sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} + \sqrt {2{b^2} + 3bc + 2{c^2}} {\rm{ \;}} + \sqrt {2{c^2} + 3ca + 2{a^2}} {\rm{ \;}} \ge \frac{{\sqrt 7 }}{2}\left( {a + b + b + c + c + a} \right)}\\{ \Rightarrow \sqrt {2{a^2} + 3ab + 2{b^2}} {\rm{ \;}} + \sqrt {2{b^2} + 3bc + 2{c^2}} {\rm{ \;}} + \sqrt {2{c^2} + 3ca + 2{a^2}} {\rm{ \;}} \ge \sqrt 7 \left( {a + b + c} \right) = 3\sqrt 7 {\mkern 1mu} {\mkern 1mu} \left( {dpcm} \right)}\end{array}$

Dấu “=” xảy ra $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a - b = 0}\\{b - c = 0}\\{c - a = 0}\\{\sqrt a {\rm{ \;}} + \sqrt b {\rm{ \;}} + \sqrt c {\rm{ \;}} = 3}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = b = c}\\{3\sqrt a {\rm{ \;}} = 3}\end{array}} \right. \Leftrightarrow a = b = c = 1$.

Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Ninh Bình năm 2023 timdapan.com"