Đề thi vào 10 môn Toán Nam Định năm 2019

Đề bài

Câu 1: Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {1 - m} \right)x + m + 1\) đồng biến trên \(\mathbb{R}.\)

A. \(m > 1\)                             B. \(m < 1\)                             C. \(m <  - 1\)                                     D. \(m >  - 1\)  

Câu 2: Phương trình \({x^2} - 2x - 1 = 0\) có hai nghiệm \({x_1},\,\,{x_2}.\) Tính \({x_1} + {x_2}.\)  

A. \({x_1} + {x_2} = 2\)                     B. \({x_1} + {x_2} = 1\)                      C. \({x_1} + {x_2} =  - 2\)                  D. \({x_1} + {x_2} =  - 1\)   

Câu 3: Cho điểm \(M\left( {{x_M};\,\,{y_M}} \right)\) thuộc đồ thị hàm số \(y =  - 3{x^2}.\) Biết \({x_M} =  - 2.\) Tính \({y_M}.\)  

A. \({y_M} = 6\)                                 B. \({y_M} =  - 6\)                              C. \({y_M} =  - 12\)                D. \({y_M} = 12\)    

Câu 4: Hệ phương trình \(\left\{ \begin{array}{l}x - y = 2\\3x + y = 1\end{array} \right.\) có bao nhiêu nghiệm?

A.  0                                        B.  1                                        C. 2                                         D. vô số.

Câu 5: Với các số \(a,\,\,b\) thỏa mãn \(a < 0,\,\,b < 0\) thì biểu thức \(a\sqrt {ab} \) bằng:

A.  \( - \sqrt {{a^2}b} \)                                 B. \(\sqrt {{a^3}b} \)                                      C. \(\sqrt {{a^2}b} \)                                  D. \( - \sqrt {{a^3}b} \)  

Câu 6: Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,\,\,AC = 4cm.\) Tính độ dài đường cao \(AH\) của tam giác \(ABC.\)  

A. \(AH = \dfrac{{12}}{7}cm\)                     B.  \(AH = \dfrac{5}{2}cm\)              C. \(AH = \dfrac{{12}}{5}cm\)               D.  \(AH = \dfrac{7}{2}cm\)  

Câu 7: Cho đường tròn tâm \(O\) bán kính \(R = 2cm\) và đường tròn tâm \(O'\) bán kính \(R' = 3cm.\) Biết \(OO' = 6cm.\) Số tiếp tuyến chung của hai đường tròn đã cho là:

A. 1                                         B. 2                                         C. 3                                         D. 4

Câu 8: Một quả bóng hình cầu có đường kính bằng \(4cm.\) Thể tích quả bóng là:

A. \(\dfrac{{32\pi }}{3}\,\,c{m^3}\)                          B. \(\dfrac{{32}}{3}\,\,c{m^3}\)                                C. \(\dfrac{{256\pi }}{3}\,\,c{m^3}\)                             D. \(\dfrac{{256}}{3}\,\,c{m^3}\)  

II. TỰ LUẬN (8 điểm)

Câu 1 (1,5 điểm)

a) Rút gọn biểu thức \(A = \sqrt {3 - 2\sqrt 2 }  - \sqrt {3 + 2\sqrt 2 } \).

b) Chứng minh rằng \(\left( {\dfrac{2}{{\sqrt a  + 3}} - \dfrac{1}{{\sqrt a  - 3}} + \dfrac{6}{{a - 9}}} \right)\left( {\sqrt a  + 3} \right) = 1\) với \(a \ge 0\) và \(a \ne 9\).

Câu 2 (1,5 điểm):

Cho phương trình \({x^2} - \left( {m - 2} \right)x - 6 = 0\,\,\,\,\,\left( 1 \right)\)  (với \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) với \(m = 0.\)

b) Chứng minh rằng với mọi giá trị của \(m\) phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.

c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_2^2 - {x_1}{x_2} + \left( {m - 2} \right){x_1} = 16.\)

Câu 3 (1 điểm):   Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} - xy + y - 7 = 0\\{x^2} + xy - 2y = 4\left( {x - 1} \right)\end{array} \right..\)

Câu 4 (3,0 điểm)

Qua điểm A nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là hai tiếp điểm). Gọi E là trung điểm của AC, F là giao điểm thứ hai của EB với đường tròn \(\left( O \right)\).

a) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp, tam giác \(CEF\) đồng dạng với tam giác \(BEC\).

b) Gọi K là giao điểm thứ hai của đường thẳng AF với đường tròn \(\left( O \right)\). Chứng minh \(BF.CK = BK.CF\).

c) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

Câu 5 (1 điểm):

Xét các số \(x,\,\,y,\,\,z\) thay đổi thỏa mãn \({x^3} + {y^3} + {z^3} - 3xyz = 2.\) Tìm giá trị nhỏ nhất của biểu thức:

\(P = \dfrac{1}{2}{\left( {x + y + z} \right)^2} + 4\left( {{x^2} + {y^2} + {z^2} - xy - yz - zx} \right).\) 

---

Lời giải chi tiết

PHẦN I: TRẮC NGHIỆM:

1. B	2. A	3. C	4. B
5. D	6. C	7. D	8. A

 

Câu 1 - Hàm số bậc nhất

Phương pháp:

Hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) đồng biến trên \(\mathbb{R}\) khi \(a > 0\) và nghịch biến trên \(\mathbb{R}\) khi \(a < 0.\)

Cách giải:

Hàm số \(y = \left( {1 - m} \right)x + m + 1\) đồng biến trên \(\mathbb{R} \Leftrightarrow 1 - m > 0 \Leftrightarrow m < 1.\)

Chọn B.

Câu 2 - Hệ thức Vi-ét và ứng dụng

Phương pháp:

Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) thì theo hệ thức Vi-et ta có: \({x_1} + {x_2} =  - \dfrac{b}{a}.\)

Cách giải:

Phương trình \({x^2} - 2x - 1 = 0\) có hai nghiệm \({x_1} + {x_2}.\)

Khi đó theo hệ thức Vi-et ta có: \({x_1} + {x_2} = 2.\)

Chọn A.

Câu 3 - Đồ thị hàm số y = ax^2 (a ≠ 0)

Phương pháp:

Điểm \(M\left( {{x_0};\,\,{y_0}} \right)\) thuộc đồ thị hàm số \(y = a{x^2}\,\,\,\left( {a \ne 0} \right) \Rightarrow {y_0} = ax_0^2.\)

Cách giải:  

Điểm \(M\left( {{x_M};\,\,{y_M}} \right)\) có hoành độ \({x_M} =  - 2\) và thuộc đồ thị hàm số \(y =  - 3{x^2}\)

\( \Rightarrow {y_M} =  - 3.{\left( { - 2} \right)^2} =  - 1.\)

Chọn C.

Câu 4 - Giải hệ phương trình bằng phương pháp cộng đại số

Phương pháp:

Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

Ta có: \(\left\{ \begin{array}{l}x - y = 2\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x = 3\\y = x - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{3}{4}\\y =  - \dfrac{5}{4}\end{array} \right.\)

Vậy hệ phương trình đã cho có nghiệm duy nhất.

Chọn B.

Câu 5 - Liên hệ giữa phép nhân và phép khai phương

Phương pháp:

Sử dụng công thức \(A\sqrt B  = \left\{ \begin{array}{l}\sqrt {{A^2}B} \,\,\,\,khi\,\,\,A \ge 0\\ - \sqrt {{A^2}B} \,\,\,khi\,\,\,A < 0\end{array} \right..\)

Cách giải:

Ta có: \(a\sqrt {ab}  =  - \sqrt {{a^2}.ab}  =  - \sqrt {{a^3}b} \) vì \(a < 0.\)

Chọn D.

Câu 6 - Một số hệ thức về cạnh và đường cao trong tam giác vuông

Phương pháp:

Sử dụng công thức hệ thức lượng trong tam giác vuông: \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}.\)

Cách giải:

 

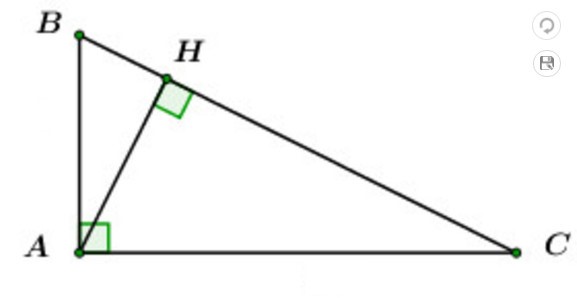
Áp dụng hệ thức lượng trong \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\) ta có:

\(\begin{array}{l}\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} + \dfrac{1}{{{4^2}}} = \dfrac{{25}}{{144}}\\ \Rightarrow A{H^2} = \dfrac{{144}}{{25}} \Rightarrow AH = \dfrac{{12}}{5}\,\,cm.\end{array}\)

Chọn C.

Câu 7 - Vị trí tương đối của hai đường tròn

Phương pháp:

Cho hai đường tròn \(\left( {O;\,\,R} \right)\) và \(\left( {O';\,\,R'} \right)\) khi đó ta có:

+) \(OO' > R + R'\) thì hai đường tròn nằm ngoài nhau hay hai đường tròn không có điểm chung.

\( \Rightarrow \) Hai đường tròn có \(4\) tiếp tuyến chung.

+) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn đựng nhau hay hai đường tròn không có điểm chung.

\( \Rightarrow \) Hai đường tròn không có tiếp tuyến chung.

+) \(\left| {R - R'} \right| < OO' < R + R'\) thì hai đường tròn cắt nhau hay hai đường tròn có hai điểm chung.

\( \Rightarrow \) Hai đường tròn có \(2\) tiếp tuyến chung.

+) \(OO' = R + R'\) thì hai đường tròn tiếp xúc ngoài hay hai đường tròn có một điểm chung.

\( \Rightarrow \) Hai đường tròn có \(1\) tiếp tuyến chung.

+) \(OO' < \left| {R - R'} \right|\) thì hai đường tròn tiếp xúc trong hay hai đường tròn có một điểm chung.

\( \Rightarrow \) Hai đường tròn có \(1\) tiếp tuyến chung.

Cách giải:

Ta có: \(OO' = 6cm\)

Lại có: \(\left\{ \begin{array}{l}R' = 3cm\\R = 2cm\end{array} \right. \Rightarrow R' + R = 3 + 2 = 5cm < OO'\)

\( \Rightarrow \) Hai đường tròn nằm ngoài nhau

\( \Rightarrow \) Hai đường tròn có \(4\) tiếp tuyến chung.

Chọn D.

Câu 8 - Hình cầu - Diện tích mặt cầu và thể tích mặt cầu

Phương pháp:

Thể tích mặt cầu bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\) 

Cách giải:

Bán kính của quả bóng là: \(4:2 = 2cm.\)

Thể tích của quả bóng đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}\,\,c{m^3}.\)

Chọn A.

PHẦN II: TỰ LUẬN

Câu 1 - Ôn tập chương 1: Căn bậc hai. Căn bậc ba

Phương pháp:

a) Sử dụng hằng đẳng thức.

b) Quy đồng, rút gọn.

Cách giải:

a) Rút gọn biểu thức \(A = \sqrt {3 - 2\sqrt 2 }  - \sqrt {3 + 2\sqrt 2 } \).

Ta có:

\(\begin{array}{l}3 - 2\sqrt 2  = {\left( {\sqrt 2 } \right)^2} - 2.\sqrt 2 .1 + {1^2} = {\left( {\sqrt 2  - 1} \right)^2}\\3 + 2\sqrt 2  = {\left( {\sqrt 2 } \right)^2} + 2.\sqrt 2 .1 + {1^2} = {\left( {\sqrt 2  + 1} \right)^2}\end{array}\)

\(\begin{array}{l} \Rightarrow A = \sqrt {3 - 2\sqrt 2 }  - \sqrt {3 + 2\sqrt 2 } \\\,\,\,\,\,\,A = \sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \sqrt {{{\left( {\sqrt 2  + 1} \right)}^2}} \\\,\,\,\,\,\,A = \left| {\sqrt 2  - 1} \right| - \left| {\sqrt 2  + 1} \right|\\\,\,\,\,\,\,A = \left( {\sqrt 2  - 1} \right) - \left( {\sqrt 2  + 1} \right)\,\,\left( {Do\,\,\sqrt 2  - 1 > 0;\,\,\sqrt 2  + 1 > 0} \right)\\\,\,\,\,\,A = \sqrt 2  - 1 - \sqrt 2  - 1 =  - 2\end{array}\) 

Vậy \(A =  - 2\).

b) Chứng minh rằng \(\left( {\dfrac{2}{{\sqrt a  + 3}} - \dfrac{1}{{\sqrt a  - 3}} + \dfrac{6}{{a - 9}}} \right)\left( {\sqrt a  + 3} \right) = 1\) với \(a \ge 0\) và \(a \ne 9\).

Với \(a \ge 0\) và \(a \ne 9\) ta có:

\(\begin{array}{l}VT = \left( {\dfrac{2}{{\sqrt a  + 3}} - \dfrac{1}{{\sqrt a  - 3}} + \dfrac{6}{{a - 9}}} \right)\left( {\sqrt a  + 3} \right)\\\,\,\,\,\,\,\, = \dfrac{{2\left( {\sqrt a  - 3} \right) - \left( {\sqrt a  + 3} \right) + 6}}{{\left( {\sqrt a  - 3} \right)\left( {\sqrt a  + 3} \right)}}\left( {\sqrt a  + 3} \right)\\\,\,\,\,\,\, = \dfrac{{2\sqrt a  - 6 - \sqrt a  - 3 + 6}}{{\sqrt a  - 3}}\\\,\,\,\,\,\, = \dfrac{{\sqrt a  - 3}}{{\sqrt a  - 3}} = 1 = VP\end{array}\)

Vậy \(\left( {\dfrac{2}{{\sqrt a  + 3}} - \dfrac{1}{{\sqrt a  - 3}} + \dfrac{6}{{a - 9}}} \right)\left( {\sqrt a  + 3} \right) = 1\) với \(a \ge 0\) và \(a \ne 9\).

Câu 2 - Ôn tập chương 4: Hàm số y = ax^2 (a ≠ 0) - Phương trình bậc hai một ẩn

Phương pháp:

a) Thay \(m = 0\) vào phương trình và giải phương trình bậc hai.

b) Chứng minh phương trình có \(\Delta  > 0\) với mọi \(m.\)

c) Áp dụng định lý Vi-et và biểu thức bài cho để làm bài toán.

Cách giải:

Cho phương trình \({x^2} - \left( {m - 2} \right)x - 6 = 0\,\,\,\,\,\left( 1 \right)\)  (với \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) với \(m = 0.\)

Thay \(m = 0\) vào phương trình \(\left( 1 \right)\) ta có: \(\left( 1 \right) \Leftrightarrow {x^2} + 2x - 6 = 0\)

Phương trình có: \(\Delta ' = 1 + 6 = 7 > 0\)

\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} =  - 1 + \sqrt 7 \\{x_2} =  - 1 - \sqrt 7 \end{array} \right..\)

Vậy với \(m = 0\) thì phương trình \(\left( 1 \right)\) có tập nghiệm: \(S = \left\{ { - 1 - \sqrt 7 ;\,\, - 1 + \sqrt 7 } \right\}.\)

b) Chứng minh rằng với mọi giá trị của \(m\) phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt.

Phương trình \(\left( 1 \right)\) có: \(\Delta  = {\left( {m - 2} \right)^2} + 4.6 = {\left( {m - 2} \right)^2} + 24\)

Vì \({\left( {m - 2} \right)^2} \ge 0\,\,\forall m \Rightarrow {\left( {m - 2} \right)^2} + 24 > 0\,\,\forall m \Leftrightarrow \Delta  > 0\,\,\forall m\)

Vậy phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt với mọi \(m.\)

c) Gọi \({x_1},\,\,{x_2}\) là hai nghiệm của phương trình \(\left( 1 \right).\) Tìm tất cả các giá trị của \(m\) để \(x_2^2 - {x_1}{x_2} + \left( {m - 2} \right){x_1} = 16.\)

Với mọi \(m\) thì  phương trình \(\left( 1 \right)\) luôn có hai nghiệm phân biệt \({x_1},\,\,{x_2}.\)

Áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m - 2\\{x_1}{x_2} =  - 6\end{array} \right..\)

Ta có \({x_1}\) là nghiệm của phương trình \(\left( 1 \right) \Rightarrow x_1^2 - \left( {m - 2} \right){x_1} - 6 = 0 \Leftrightarrow \left( {m - 2} \right){x_1} = x_1^2 - 6\,\,\,\left( * \right)\)

Theo đề bài ta có: \(x_2^2 - {x_1}{x_2} + \left( {m - 2} \right){x_1} = 16\,\,\,\,\left( {**} \right)\)

Thay \(\left( * \right)\)  vào \(\left( {**} \right)\) ta được:

\(\begin{array}{l}\left( {**} \right) \Leftrightarrow x_2^2 - {x_1}{x_2} + x_1^2 - 6 = 16\\ \Leftrightarrow x_1^2 + 2{x_1}{x_2} + x_2^2 - 3{x_1}{x_2} = 22\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2} = 22\\ \Leftrightarrow {\left( {m - 2} \right)^2} - 3.\left( { - 6} \right) = 22\\ \Leftrightarrow {\left( {m - 2} \right)^2} = 4\\ \Leftrightarrow \left[ \begin{array}{l}m - 2 = 2\\m - 2 =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 4\\m = 0\end{array} \right..\end{array}\)

Vậy \(m = 0,\,\,m = 4\) là các giá trị thỏa mãn bài toán.

Câu 3 - Hệ phương trình không mẫu mực

Phương pháp:

+) Cộng vế với vế của hệ phương trình.

+) Giải hệ phương trình bằng phương pháp thế.

Cách giải: 

Giải hệ phương trình \(\left\{ \begin{array}{l}{x^2} - xy + y - 7 = 0\\{x^2} + xy - 2y = 4\left( {x - 1} \right)\end{array} \right..\)

\(\begin{array}{l}\,\,\,\,\,\,\,\,\left\{ \begin{array}{l}{x^2} - xy + y - 7 = 0\\{x^2} + xy - 2y = 4\left( {x - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - y - 7 = 4x - 4\\{x^2} - xy + y - 7 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 2{x^2} - 4x - 3\,\,\,\,\left( 1 \right)\\{x^2} - x\left( {2{x^2} - 4x - 3} \right) + 2{x^2} - 4x - 3 - 7 = 0\,\,\,\,\left( 2 \right)\end{array} \right.\end{array}\)

Giải phương trình \(\left( 2 \right)\) ta được:

\(\begin{array}{l}\left( 2 \right) \Leftrightarrow {x^2} - 2{x^3} + 4{x^2} + 3x + 2{x^2} - 4x - 10 = 0\\ \Leftrightarrow  - 2{x^3} + 7{x^2} - x - 10 = 0\\ \Leftrightarrow 2{x^3} - 7{x^2} + x + 10 = 0\\ \Leftrightarrow 2{x^3} + 2{x^2} - 9{x^2} - 9x + 10x + 10 = 0\\ \Leftrightarrow 2{x^2}\left( {x + 1} \right) - 9x\left( {x + 1} \right) + 10\left( {x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {2{x^2} - 9x + 10} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {2{x^2} - 4x - 5x + 10} \right) = 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left( {x + 1} \right)\left[ {2x\left( {x - 2} \right) - 5\left( {x - 2} \right)} \right] = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {2x - 5} \right)\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\2x - 5 = 0\\x - 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = \dfrac{5}{2}\\x = 2\end{array} \right..\end{array}\)

+) Với \(x =  - 1 \Rightarrow \left( 1 \right) \Leftrightarrow y = 2.{\left( { - 1} \right)^2} - 4.\left( { - 1} \right) - 3 = 3.\)

+) Với \(x = \dfrac{5}{2} \Rightarrow \left( 1 \right) \Leftrightarrow y = 2.{\left( {\dfrac{5}{2}} \right)^2} - 4.\dfrac{5}{2} - 3 =  - \dfrac{1}{2}.\)

+) Với \(x = 2 \Rightarrow \left( 1 \right) \Leftrightarrow y = {2.2^2} - 4.2 - 3 =  - 3.\)

Vậy hệ phương trình có tập nghiệm: \(S = \left\{ {\left( { - 1;\,\,3} \right);\,\,\left( {2; - 3} \right);\,\,\left( {\dfrac{5}{2}; - \dfrac{1}{2}} \right)} \right\}.\)

Câu 4 - Ôn tập tổng hợp chương 1, 2, 3 - Hình học

Phương pháp:

a) Chứng minh tứ giác nội tiếp bằng các dấu hiệu nhận biết.

+) Chứng minh tam giác đồng dạng theo trường hợp góc – góc.

b) Chứng minh các tam giác đồng dạng và dựa vào tính chất hai tiếp tuyến cắt nhau để chứng minh đẳng thức bài yêu cầu.

Cách giải:

 

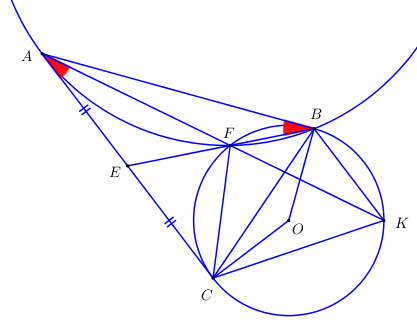
a) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp, tam giác \(CEF\) đồng dạng với tam giác \(BEC\).

+) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp:

Do \(AB,\,\,AC\) là tiếp tuyến của \(\left( O \right)\,\,\left( {gt} \right) \Rightarrow AB \bot OB;\,\,AC \bot OC \Rightarrow \angle OBA = \angle OCA = {90^0}\).

Xét tứ giác \(ABOC\) có: \(\angle OBA + \angle OCA = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(ABOC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

+) Chứng minh  

Xét đường tròn \(\left( O \right)\) ta có:

\(\angle EOF\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(CF.\)

\(\angle FBC\) là góc nội tiếp chắn cung \(CF.\)

\( \Rightarrow \angle ECF = \angle CBF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CF\))

Xét \(\Delta CEF\) và \(\Delta BEC\) ta có:

 

b) Gọi K là giao điểm thứ hai của đường thẳng AF với đường tròn \(\left( O \right)\). Chứng minh \(BF.CK = BK.CF\).

Xét tam giác \(ABF\) và tam giác \(AKB\) có:

\(\angle BAK\,\,\,chung\)

\(\angle ABF = \angle AKB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BF\));

 (các cặp cạnh tương ứng tỉ lệ).

Xét tam giác \(ACF\) và tam giác \(AKC\) có:

\(\angle CAK\) chung;

\(\angle ACF = \angle AKC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(CF\));

 (các cặp cạnh tương ứng tỉ lệ).

Mà \(AB = AC\) (tính chất 2 tiếp tuyến cắt nhau) nên \(\dfrac{{AF}}{{AB}} = \dfrac{{AF}}{{AC}}\) (3).

Từ (1), (2) và (3) suy ra \(\dfrac{{BF}}{{BK}} = \dfrac{{CF}}{{CK}} \Rightarrow BF.CK = BK.CF\).

c) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

Xét tam giác \(ECF\) và ta giác \(EBC\) có:

\(\angle BEC\) chung;

\(\angle ECF = \angle EBC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(CF\))

.

Mà \(EC = EA\,\,\left( {gt} \right) \Rightarrow E{A^2} = EB.EF \Rightarrow \dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\).

Xét tam giác \(BEA\) và tam giác \(AEF\) có:

\(\begin{array}{l} & \dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\,\,\left( {cmt} \right)\\ & \angle AEB\,\,\,\,chung\end{array}\)

  (hai góc tương ứng)

Mà góc \(\angle ABE\) là góc nội tiếp chắn cung \(AF\) của đường tròn ngoại tiếp tam giác \(ABF\); \(\angle FAE\) ở vị trí góc tạo bởi tiếp tuyến và dây cung chắn cung \(AF\)).

Vậy \(AE\) là  tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

Câu 5 - Tìm giá trị lớn nhất, giá trị nhỏ nhất

Phương pháp:

Biến đổi biểu thức bài cho, đặt \(x + y + z = t\,\,\left( {t > 0} \right).\)

Áp dụng bất đẳng thức Cô-si cho 3 số.

Cách giải:

Theo đề bài ta có: \({x^3} + {y^3} + {z^3} - 3xyz = 2\)

\(\begin{array}{l} \Leftrightarrow \left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - yz - zx} \right) = 2\\ \Leftrightarrow \left( {x + y + z} \right)\left( {2{x^2} + 2{y^2} + 2{z^2} - 2xy - 2yz - 2zx} \right) = 4\\ \Leftrightarrow \left( {x + y + z} \right)\left[ {\left( {{x^2} - 2xy + {y^2}} \right) + \left( {{y^2} - 2yz + {z^2}} \right) + \left( {{z^2} - 2zx + {x^2}} \right)} \right] = 4\\ \Leftrightarrow \left( {x + y + z} \right)\left[ {{{\left( {x - y} \right)}^2} + {{\left( {y - z} \right)}^2} + {{\left( {z - x} \right)}^2}} \right] = 4\,\,\,\,\left( * \right)\end{array}\)

Ta có: \({\left( {x - y} \right)^2} + {\left( {y - z} \right)^2} + {\left( {z - x} \right)^2} \ge 0\,\,\forall x,\,\,y,\,\,z\)

\( \Rightarrow x + y + z > 0.\)

Đặt \(x + y + z = t\,\,\,\left( {t > 0} \right) \Rightarrow {x^2} + {y^2} + {z^2} - xy - yz - zx = \dfrac{2}{t}.\)

\( \Rightarrow P = \dfrac{1}{2}{t^2} + \dfrac{8}{t} = \dfrac{{{t^2}}}{2} + \dfrac{4}{t} + \dfrac{4}{t}\)

Áp dụng bất đẳng thức Cô-si cho ba số dương \(\dfrac{{{t^2}}}{2};\,\,\dfrac{4}{t};\,\,\dfrac{4}{t}\) ta có:

\(P = \dfrac{{{t^2}}}{2} + \dfrac{4}{t} + \dfrac{4}{t} \ge 3\sqrt[3]{{\dfrac{{{t^2}}}{2}.\dfrac{4}{t}.\dfrac{4}{t}}} = 3.\sqrt[3]{8} = 6.\)

Dấu “=” xảy ra \( \Leftrightarrow \dfrac{{{t^2}}}{2} = \dfrac{4}{t} \Leftrightarrow {t^3} = 8 \Leftrightarrow t = 2\) \( \Rightarrow x + y + z = 2.\) 

Vậy \(Min\,\,P = 6\)  khi \(\left\{ \begin{array}{l}x + y + z = 2\\{x^3} + {y^3} + {z^3} - 3xyz = 2\end{array} \right..\)