Đề thi vào 10 môn Toán Khánh Hòa năm 2023

Đề bài

Câu 1: Không sử dụng máy tính cầm tay

a) Rút gọn biểu thức \(A = \sqrt {25}  + \sqrt {16}  - \sqrt 4 \)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + y = 8\\2x - y = 1\end{array} \right.\)

Câu 2: Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right):y = 6x + 2023\) và parabol \(\left( P \right):y = {x^2}\)

a) Vẽ parabol \(\left( P \right).\)

b) Chứng minh \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.

c) Gọi \({x_1}\) và \({x_2}\) là hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right).\) Tính \({x_1} + {x_2}\) và \({x_1} \cdot {x_2}.\) Từ đó lập phương trình bậc hai ẩn t có hai nghiệm \({t_1} = {x_1} + 2{x_2}\) và \({t_2} = {x_2} + 2{x_1}.\)

Câu 3: 

a) Hưởng ứng phong trào “Ngày Chủ nhật xanh” do Tỉnh đoàn phát động, Trường THCS X chọn 15 học sinh chia thành hai tổ tham gia trồng cây. Tổ 1 trồng được 30 cây, tổ II trồng được 36 cây. Biết rằng mỗi học sinh ở tổ I trồng được nhiều hơn mỗi học sinh ở tổ II là 1 cây. Hỏi mỗi tổ có bao nhiêu học sinh?

b) Gạch xây 3 lỗ (như hình vẽ) được làm bằng đất nung, thường được sử dụng trong các công trình xây dựng có dạng hình hộp chữ nhật với chiều dài 220 mm, chiều rộng 105 mm, chiều cao 60 mm. Mỗi lỗ là hình trụ có trục song song với chiều cao viên gạch, đường kính đáy là 14 mm. Tính thể tích phần đất nung của một viên gạch. Biết \(V = a \cdot b \cdot c;\,\,V = \pi  \cdot {r^2} \cdot h\) lần lượt là công thức tính hình hộp chữ nhật và hình trụ (trong đó a, b, c là ba kích thước của hình hộp chữ nhật, r là bán kính đường tròn đáy, h là chiều cao hình trụ; lấy \(\pi  \approx 3,14\)).

Câu 4: Cho đường tròn\(\left( O \right)\)đường kính AB và điểm C thuộc đường tròn sao cho \(AC < BC\) (C khác A). Vẽ CH vuông góc với \(AB\,\,\left( {H \in AB} \right).\)

a) Chứng minh \(\Delta \,ABC\) là tam giác vuông. Tính AC, biết AB = 4 cm, AH = 1 cm.

b) Trên tia đối của tia CA lấy điểm D sao cho \(CD = CA.\) Vẽ DE vuông góc với \(AB\,\,\left( {E \in AB} \right).\) Chứng minh  BECD là tứ giác nội tiếp.

c) Gọi I là giao điểm của DE và BC, K là điểm đối xứng của I qua C, tiếp tuyến của  tại C cắt KA tại M. Chứng minh KA là tiếp tuyến của \(\left( O \right)\)và đi qua trung điểm của CH.

Câu 5: Trong quá trình thiết kế công viên thiếu nhi, kĩ sư sử dụng mảnh đất hình chữ nhật có diện tích 600 m² để làm bãi đỗ xe. Một cạnh của mảnh đất được xây bằng tường gạch với mỗi mét chiều dài chi phí hết 280 000 đồng, ba cạnh còn lại được rào bằng một loại thép với mỗi mét chiều dài chi phí hết 140 000 đồng, trong đó có mở cổng rộng 5 m (như hình vẽ). Tìm chu vi của mảnh đất sao cho chi phí làm hàng rào là ít nhất.

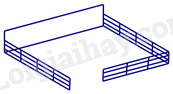
-----HẾT-----

---

Lời giải chi tiết

Câu 1 (TH):

Phương pháp:

a) Khai căn và thực hiện tính.

b) Giải hệ phương trình bằng phương pháp cộng đại số.

Cách giải:

a) \(A = \sqrt {25}  + \sqrt {16}  - \sqrt 4  = 5 + 4 - 2 = 7.\)

b) \(\left\{ \begin{array}{l}x + y = 8\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\x + y = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 5\end{array} \right..\)

Vậy hệ phương trình có nghiệm duy nhất là \(\left( {x;y} \right) = \left( {3;5} \right)\)

Câu 2 (VD):

Phương pháp:

a) Viết bảng giá trị và vẽ parabol (P).

b) Xét phương trình hoành độ và chứng minh \(\Delta  > 0\) hoặc chứng minh a.c < 0.

c) Áp dụng hệ thức vi-et \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{b}{a}\\{x_1} \cdot {x_2} = \frac{c}{a}\end{array} \right.\)

Cách giải:

a) Bảng giá trị

Đồ thị

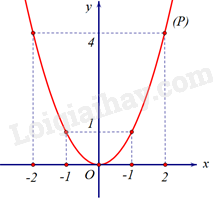
b) Phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right):\)

\({x^2} = 6x + 2023 \Leftrightarrow {x^2} - 6x - 2023 = 0\,\,\,\,\,\,\,\,\left( * \right)\)

Vì \(\Delta  = {\left( { - 6} \right)^2} - 4 \cdot 1 \cdot \left( { - 2023} \right) = 8128 > 0\) nên phương trình (*) có hai nghiệm phân biệt.

Vậy \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt.

Cách 2:

Ta có: \(a.c = 1.( - 2023) =  - 2023 < 0\)

Nên phương trình luôn có hai nghiệm phân biệt trái dấu

Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.

c) Theo Vi-et ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \frac{{ - 6}}{1} = 6\\{x_1} \cdot {x_2} =  - 2023.\end{array} \right.\)

Suy ra: \(\left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ =  (}}{x_1}{\rm{ +  2}}{x_2}{\rm{)  +   (}}{x_2}{\rm{ +  2}}{x_1})\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = {\rm{(}}{x_1}{\rm{ +  2}}{x_2}{\rm{)}}{\rm{.(}}{x_2}{\rm{ +  2}}{x_1})\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ =  }}{x_1}{\rm{ +  2}}{x_2}{\rm{  +   }}{x_2}{\rm{ +  2}}{x_1}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = {x_1}{x_2}{\rm{ +  2}}x_1^2{\rm{ +  2}}x_2^2 + 4{x_1}{x_2}\end{array} \right.\)                  

\( \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{x_1}{\rm{ +  3}}{x_2}{\rm{ }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5{x_1}{x_2}{\rm{ +  2}}\left( {x_1^2{\rm{ +  }}x_2^2} \right)\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{\rm{.(}}{x_1}{\rm{ +  }}{x_2}{\rm{) }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5{x_1}{x_2}{\rm{ +  2}}\left[ {{{\left( {{x_1}{\rm{ +  }}{x_2}} \right)}^2} - 2{x_1}{x_2}} \right]\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{\rm{.6 }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5.( - 2023){\rm{ +  2}}\left[ {{6^2} - 2.( - 2023)} \right]\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 18 }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} =  - 1951\end{array} \right.\)

Đặt  \({\rm{S =  }}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 18}}\)  ;  \({\rm{P =  }}{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} =  - 1951\)

Do \({{\rm{S}}^2} - 4.P = {18^2} - 4.( - 1951) = 8128 > 0\) nên theo định lí Vi-et đảo ta có \({{\rm{t}}_1}{\rm{ ; }}{{\rm{t}}_2}\) là hai nghiệm của phương trình bậc hai:  \({t^2} - S.t + P = 0\)

                                         \( \Leftrightarrow {t^2} - 18t - 1951 = 0\)

Vậy phương trình bậc hai ẩn t cần tìm là: \({t^2} - 18t - 1951 = 0\)

Câu 3 (VD):

Phương pháp:

a)

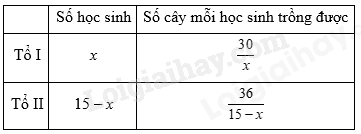
Mỗi học sinh ở tổ I trồng được nhiều hơn mỗi học sinh ở tổ II là 1 cây nên ta có phương trình:

\(\frac{{30}}{x} - \frac{{36}}{{15 - x}} = 1\)

b) Áp dụng công thức:

- Thể tích hình hộp chữ nhật: \(V = a.b.c\)

- Thể tích hình trụ: \(V = \pi {r^2}h\)

Cách giải:

a) Gọi số học sinh của Tổ I là \(x\) (học sinh) \(\left( {x \in N*;x < 15} \right)\)

Khi đó, số học sinh của Tổ II là \(15 - x\) (học sinh)

Mỗi học sinh tổ I trồng được \(\frac{{30}}{x}\) (cây)

Mỗi học sinh tổ II trồng được \(\frac{{36}}{{15 - x}}\) (cây)

Theo đề bài, ta có phương trình : \(\frac{{30}}{x} - \frac{{36}}{{15 - x}} = 1\)

\( \Leftrightarrow 30.(15 - x) - 36x = 1.x.(15 - x)\)

\( \Leftrightarrow 450 - 30x - 36x = 15x - {x^2}\)

\( \Leftrightarrow {x^2} - 15x + 450 - 30x - 36x = 0\)

\( \Leftrightarrow {x^2} - 81x + 450 = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}{x_1} = 75\,\,(L) & \\{x_2} = 6 & (tm)\end{array} \right.\)

Vậy tổ I có 6 học sinh; tổ II có 15 – 6 = 9 học sinh.

b) Thể tích viên gạch hình hộp chữ nhật khi chưa khoét lỗ là:

\({V_1} = a.b.c = 220.105.60 = 1386000\) (mm³)

Thể tích mỗi lỗ hình trụ trong viên gạch là:

\({V_2} = \pi {r^2}h = \pi .{\left( {\frac{{40}}{2}} \right)^2}.60 = 9231,6\) (mm³)

Thể tích phần đất nung của viên gạch là:

\(V = {V_1} - 3.{V_2} = 1386000 - 3.9231,6 = 1358305,2\)(mm³)

Vậy thể tích phần đất nung của viên gạch là 1358305,2 mm³.

Câu 4 (TH):

Phương pháp:

a) Áp dụng hệ thức lượng trong tam giác vuông để tính AC.

b) Tứ giác có hai đỉnh kề cùng nhìn một cạnh dưới một góc bằng nhau thì là tứ giác nội tiếp.

c) Chứng minh \(BM\) đi qua trung điểm của \(CH\) từ đó gọi \(U\) là giao điểm của \(CH\) và \(MB\), ta chứng minh \(MK = AM\) \( \Rightarrow CU = HU\) và kết luận.

Cách giải:

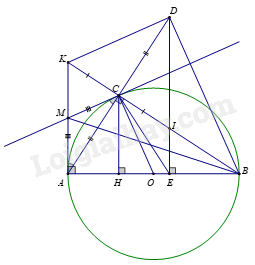
a)  Xét đường tròn (O) có \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn

\( \Rightarrow \)\(\widehat {ACB}\) = 90⁰ hay \(\Delta ABC\) vuông tại C

  \(\Delta ABC\) vuông tại \(C\) có \(CH\) là đường cao

\( \Rightarrow \)\(A{C^2} = AH.AB = 1.4 = 4\) (Hệ thức lượng trong tam giác vuông)

\( \Rightarrow AC = 2cm\)

b) Xét tứ giác \(BECD\) có \(\widehat {DCB} = \widehat {DEB} = {90^0}\)

 \( \Rightarrow \) Hai đỉnh \(C\) và \(E\) kề nhau cùng nhìn cạnh \(DB\) dưới 1 góc \({90^0}\)

Nên tứ giác \(BECD\) nội tiếp

c)  Tứ giác \(AKDI\) có \(CK = CI\) (\(K\) là điểm đối xứng của \(I\)qua \(C\)) và \(CA = CD\)

\( \Rightarrow \) Tứ giác \(AKDI\) là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường)

\( \Rightarrow \) \(AK\) // \(DI\) mà \(DI \bot AO\) tại \(E\)

\( \Rightarrow \) \(AK \bot AO\) tại \(A\)

Mà \(AO\) là bán kính của đường tròn \(\left( O \right)\) nên \(AK\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A\).

 Đường tròn \(\left( O \right)\)có \(MA,MC\) là 2 tiếp tuyến cắt nhau \( \Rightarrow \) \(MA = MC\) \(\left( 1 \right)\)

\( \Rightarrow \)\(\Delta MAC\) cân tại \(M\) \( \Rightarrow \) \(\widehat {MAC} = \widehat {MCA}\)

Mà \(\widehat {KCM} + \widehat {MCA} = {90^0}\) nên \(\widehat {KCM} + \widehat {MAC} = {90^0}\)

Mà \(\widehat {MKC} + \widehat {MAC} = {90^0}\) (\(\Delta AKC\) vuông tại \(C\)) nên \(\widehat {KCM} = \widehat {MKC}\)

\( \Rightarrow \)\(\Delta KMC\) cân tại \(M\) \( \Rightarrow \)\(MC = MK\) \(\left( 2 \right)\)

 Từ \(\left( 1 \right)\)và \(\left( 2 \right)\) \( \Rightarrow \) \(MA = MK\) hay \(BM\) đi qua trung điểm của \(CH\).

 Gọi \(U\) là giao điểm của \(CH\) và \(MB\).

 \(AK\) // \(CH\) (cùng \( \bot \) \(AB\))

\(MK\) // \(CU\)\( \Rightarrow \frac{{CU}}{{MK}} = \frac{{BU}}{{BM}}\)(Hệ quả định lý Talet) \(\left( 3 \right)\)

\(MA\)// \(UH\) \( \Rightarrow \frac{{HU}}{{AM}} = \frac{{BU}}{{BM}}\)(Hệ quả định lý Talet) \(\left( 4 \right)\)

Từ \(\left( 3 \right)\), \(\left( 4 \right)\) và \(MK = AM\) \( \Rightarrow CU = HU\) hay \(U\)là trung điểm của \(CH\)

Vậy \(BM\) đi qua trung điểm của \(CH\)

Câu 5 (VDC):

Phương pháp:

Áp dụng bất đẳng thức cô-si.

Cách giải:

Gọi x và y (m) lần lượt là độ dài cạnh được xây bằng tường và cạnh được rào bằng thép \(\left( {x,\,\,y > 0} \right)\)

Chu vi mảnh đất bằng \(2\left( {x + y} \right)\) (m)

Diện tích của mảnh đất là \(x \cdot y = 600\) (m²)

Chi phí xây tường gạch là \(280\,x\) (nghìn đồng)

Chi phí rào bằng thép là \(140\,\left( {2y + x - 5} \right)\) (nghìn đồng)

Tổng chi phí làm hàng rào là \(C = 420x + 280y - 700\) (nghìn đồng)

Áp dụng bất đẳng thức Cosi ta có:

     \(420x + 280y \ge 2\sqrt {420x \cdot 280y}  = 1\,680\,0\)

\( \Leftrightarrow C \ge 16800 - 700 = 1\,610\,0\)

Do đó \(\mathop {Min}\limits_{} C = 16\,100\, \Leftrightarrow \left\{ \begin{array}{l}420x = 280y\\xy = 600\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 2y\\x \cdot 3x = 1200\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 20\\y = 30\end{array} \right.\,\,\,\left( {TM} \right)\)

Vậy chu vi của mảnh đất để chi phí làm hàng rào nhỏ nhất là \(2\left( {x + y} \right) = 100\) (m)

-----HẾT-----