Đề thi vào 10 môn Toán Hậu Giang năm 2019
PHẦN I: TRẮC NGHIỆM (3 điểm) Câu 1: Điều kiện để hàm số
Đề bài
PHẦN I: TRẮC NGHIỆM (3 điểm)
Câu 1: Điều kiện để hàm số \(y = \left( { - m + 3} \right)x - 3\) đồng biến trên \(\mathbb{R}\) là:
A. \(m = 3\) B. \(m < 3\) C. \(m \ge 3\) D. \(x \ne 3\)
Câu 2: Cho hàm số \(y = - 3{x^2}.\) Kết luận nào sau đây đúng?
A. \(y = 0\) là giá trị lớn nhất của hàm số.
B. \(y = 0\) là giá trị nhỏ nhất của hàm số.
C. Không xác định được giá trị lớn nhất của hàm số trên.
D. Xác định được giá trị nhỏ nhất của hám số trên.
Câu 3: Điều kiện xác định của biểu thức \(\sqrt {2019 - \dfrac{{2019}}{x}} \) là:
A. \(x \ne 0\) B. \(x \ge 1\) C. \(\left[ \begin{array}{l}x \ge 1\\x < 0\end{array} \right.\) D. \(0 < x \le 1\)
Câu 4: Cho phương trình \(x - 2y = 2\,\,\,\,\,\left( 1 \right).\) Phương trình nào trong các phương trình sau đây kết hợp với \(\left( 1 \right)\) để được phương trình vô số nghiệm?
A. \(2x - 3y = 3\) B. \(2x - 4y = - 4\) C. \( - \dfrac{1}{2}x + y = - 1\) D. \(\dfrac{1}{2}x - y = - 1\)
Câu 5: Biểu thức \(\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt 5 \) có kết quả là:
A. \(3 + 2\sqrt 5 \) B. \(3 - 2\sqrt 5 \) C. \(2 - 3\sqrt 5 \) D. \( - 3\)
Câu 6: Cho hai phương trình \({x^2} - 2x + a = 0\) và \({x^2} + x + 2a = 0.\) Để hai phương trình cùng vô nghiệm thì:
A. \(a > 1\) B. \(a < 1\) C. \(a > \dfrac{1}{8}\) D. \(a < \dfrac{1}{8}\)
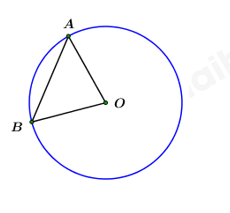
Câu 7: Cho đường tròn \(\left( {O;\,\,R} \right)\) và một dây cung \(AB = R.\) Khi đó số đo cung nhỏ \(AB\) là:
A. \({60^0}\) B. \({120^0}\) C. \({150^0}\) D. \({100^0}\)
Câu 8: Đường tròn là hình:
A. Không có trục đối xứng. B. Có một trục đối xứng.
C. Có hai trục đối xứng. D. Có vô số trục đối xứng.
Câu 9: Cho phương trình \({x^2} - x - 4 = 0\) có nghiệm \({x_1},\,\,{x_2}.\) Biểu thức \(A = x_1^3 + x_2^3\) có giá trị là:
A. \(A = 28\) B. \(A = - 13\) C. \(A = 13\) D. \(A = 18\)
Câu 10: Thể tích hình cầu thay đổi như thế nào nếu bán kính hình cầu tăng gấp 2 lần?
A. Tăng gấp 16 lần. B. Tăng gấp 8 lần.
C. Tăng gấp 4 lần. D. Tăng gấp 2 lần.
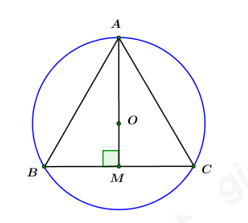
Câu 11: Diện tích hình tròn ngoại tiếp một tam giác đều cạnh \(a\) là:
A. \(\pi {a^2}\) B. \(\dfrac{{3\pi {a^2}}}{4}\) C. \(3\pi {a^2}\) D. \(\dfrac{{\pi {a^2}}}{3}\)
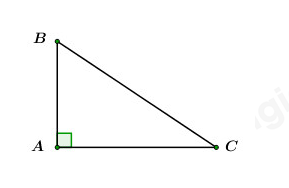
Câu 12: Cho tam giác \(ABC\) vuông tại \(A.\) Khi đó trong các khẳng định sau, khẳng định nào đúng?
A. \(\dfrac{{AB}}{{AC}} = \dfrac{{\cos C}}{{\cos B}}\) B. \(\sin B = \cos C\) C. \(\sin B = \tan C\) D. \(\tan B = \cos C\)
PHẦN II: TỰ LUẬN (7 điểm)
Câu 1 (1 điểm):
Rút gọn biểu thức sau: \(A = \dfrac{{4 + \sqrt 8 + \sqrt 2 - \sqrt 3 - \sqrt 6 }}{{2 + \sqrt 2 - \sqrt 3 }}.\)
Câu 2 (1,5 điểm):
Không sử dụng máy tính cầm tay, giải các phương trình và hệ phương trình sau:
a) \(5{x^2} + 13x - 6 = 0\) b) \({x^4} + 2{x^2} - 15 = 0\) c) \(\left\{ \begin{array}{l}3x - 4y = 17\\5x + 2y = 11\end{array} \right.\)
Câu 3 (1,5 điểm):
a) Trong mặt phẳng tọa độ \(Oxy\) vẽ parabol \(y = \dfrac{1}{2}{x^2}.\)
b) Tìm \(m\) để đường thẳng \(\left( d \right):\,\,\,y = \left( {m - 1} \right)x + \dfrac{1}{2}{m^2} + m\) đi qua điểm \(M\left( {1; - 1} \right).\)
Câu 4 (2,5 điểm) Cho đường tròn tâm \(\left( O \right)\) với dây \(AB\) cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M, N lần lượt là điểm chính giữa của cung nhỏ AB và AC. Gọi I là giao điểm của BN và CM. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K.
a) Chứng minh tứ giác BMHI nội tiếp.
b) Chứng minh \(MK.MN = MI.MC\).
c) Chứng minh tam giác AKI cân tại K.
Câu 5 (0,5 điểm): Với\(x \ne 0\), tìm giá trị nhỏ nhất của biểu thức \(A = \dfrac{{{x^2} - 3x + 2019}}{{{x^2}}}.\)
Lời giải
PHẦN I: TRẮC NGHIỆM (3 điểm)
|
1. B |
2. A |
3. C |
4. C |
5. B |
6. A |
|
7. A |
8. D |
9. C |
10. B |
11. D |
12. B |
Câu 1 (TH) - Hàm số bậc nhất
Phương pháp:
Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R} \Leftrightarrow a > 0.\)
Cách giải:
Hàm số \(y = \left( { - m + 3} \right)x - 3\) đồng biến trên \(\mathbb{R} \Leftrightarrow - m + 3 > 0 \Leftrightarrow m < 3.\)
Chọn B.
Câu 2 (TH) - Hàm số y = ax^2 (a ≠ 0)
Phương pháp:
Hàm số \(y = a{x^2}\) có \(a > 0\) đạt giá trị nhỏ nhất là \(y = 0\) và có \(a < 0\) thì hàm số đạt giá trị lớn nhất là \(y = 0.\)
Cách giải:
Ta có: \(y = - 3{x^2}\) có \(a = - 3 < 0 \Rightarrow \) hàm số đạt giá trị lớn nhất \(y = 0\) khi \(x = 0.\)
Chọn A.
Câu 3 (TH) - Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|
Phương pháp:
Biểu thức \(\sqrt {f\left( x \right)} \) xác định \( \Leftrightarrow f\left( x \right) \ge 0.\)
Cách giải:
Biểu thức \(\sqrt {2019 - \dfrac{{2019}}{x}} \) xác định
\( \Leftrightarrow 2019 - \dfrac{{2019}}{x} \ge 0 \Leftrightarrow \dfrac{{2019\left( {x - 1} \right)}}{x} \ge 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 \ge 0\\x > 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 \le 0\\x < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 1\\x < 0\end{array} \right..\)
Chọn C.
Câu 4 (VD) - Ôn tập chương 3: Hệ hai phương trình bậc nhất một ẩn
Phương pháp:
Cách 1: Hệ phương trình \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) có vô số nghiệm \( \Leftrightarrow \dfrac{a}{{a'}} = \dfrac{b}{{b'}} = \dfrac{c}{{c'}}.\)
Cách 2: Giải hệ phương trình gồm phương trình \(\left( 1 \right)\) với các phương trình ở các đáp án, hệ phương trình nào có vô số nghiệm thì chọn đáp án đó.
Cách giải:
Xét đáp án A ta có hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 2\\2x - 3y = 3\end{array} \right.\) có: \(\dfrac{1}{2} \ne \dfrac{{ - 2}}{{ - 3}} \Rightarrow \) loại đáp án A.
Xét đáp án B ta có hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 2\\2x - 4y = - 4\end{array} \right.\) có: \(\dfrac{1}{2} = \dfrac{{ - 2}}{{ - 4}} \ne \dfrac{2}{{ - 4}} \Rightarrow \) loại đáp án B.
Xét đáp án C ta có hệ phương trình: \(\left\{ \begin{array}{l}x - 2y = 2\\ - \dfrac{1}{2}x + y = - 1\end{array} \right.\) có: \(\dfrac{1}{{ - \dfrac{1}{2}}} = \dfrac{{ - 2}}{1} = \dfrac{2}{{ - 1}} = - 2 \Rightarrow \) chọn đáp án C.
Chọn C.
Câu 5 (TH) - Căn thức bậc hai và hằng đẳng thức √A^(2)=|A|
Phương pháp:
Sử dụng công thức: \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,\,A < 0\end{array} \right..\)
Cách giải:
Ta có: \(\sqrt {{{\left( {\sqrt 5 - 3} \right)}^2}} - \sqrt 5 = \left| {\sqrt 5 - 3} \right| - \sqrt 5 = 3 - \sqrt 5 - \sqrt 5 = 3 - 2\sqrt 5 .\,\,\,\,\left( {do\,\,\,\sqrt 5 - 3 < 0} \right).\)
Chọn B.
Câu 6 (TH) - Công thức nghiệm của phương trình bậc hai
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) vô nghiệm \( \Leftrightarrow \Delta < 0.\)
Cách giải:
Phương trình \({x^2} - 2x + a = 0\) vô nghiệm \( \Leftrightarrow \Delta {'_1} < 0 \Leftrightarrow 1 - a < 0 \Leftrightarrow a > 1.\)
Phương trình \({x^2} + x + 2a = 0\) vô nghiệm \( \Leftrightarrow {\Delta _2} < 0 \Leftrightarrow 1 - 8a < 0 \Leftrightarrow a > \dfrac{1}{8}.\)
Vậy với \(a > 1\) thì hai phương trình đã cho cùng vô nghiệm.
Chọn A.
Câu 7 (TH) - Góc ở tâm. Số đo cung
Phương pháp:
Công thức tính diện tích đường tròn bán kính \(R\) là: \(S = \pi {R^2}.\)
Cách giải:
Xét đường tròn \(\left( O \right)\) có dây cung \(AB = R\)
\( \Rightarrow \Delta ABC\) là tam giác đều cạnh \(R.\)
\( \Rightarrow \angle AOB = {60^0}\)
Mà \(\angle AOB\) là góc nội tiếp chắn cung
Chọn A.
Câu 8 (NB) - Sự xác định đường tròn. Tính chất đối xứng của đường tròn
Phương pháp:
Áp dụng lý thuyết sự xác định đường tròn và tính đối xứng của đường tròn để chọn đáp án đúng.
Cách giải:
Đường tròn là hình có vô số trục đối xứng vì mỗi trục đối xứng của đường tròn là một đườn kính của đường tròn.
Chọn D.
Câu 9 (TH) - Hệ thức Vi-ét và ứng dụng
Phương pháp:
Phương trình \(a{x^2} + bx + c = 0\,\,\,\,\left( {a \ne 0} \right)\) có hai nghiệm \({x_1},\,\,{x_2}.\)
Khi đó theo hệ thức Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right..\)
Cách giải:
Giả sử phương trình \({x^2} - x - 4 = 0\) có hai nghiệm \({x_1},\,\,{x_2}.\)
Khi đó áp dụng định lý Vi-et ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 4\end{array} \right..\)
\(\begin{array}{l} \Rightarrow A = x_1^3 + x_2^3 = {\left( {{x_1} + {x_2}} \right)^3} - 3{x_1}{x_2}\left( {{x_1} + {x_2}} \right)\\ = {1^3} - 3.\left( { - 4} \right) = 13.\end{array}\)
Chọn C.
Câu 10 (TH) - Hình cầu - Diện tích mặt cầu và thể tích mặt cầu
Phương pháp:
Công thức tính thể tích mặt cầu bán kính \(R\) là: \(V = \dfrac{4}{3}\pi {R^3}.\)
Cách giải:
Thể tích của hình cầu ban đầu là: \({V_1} = \dfrac{4}{3}\pi {R^3}.\)
Thể tích của hình cầu sau khi bán kính tăng lên \(2\) lần là: \({V_2} = \dfrac{4}{3}\pi {\left( {2R} \right)^3} = \dfrac{{32\pi {R^3}}}{3}.\)
\( \Rightarrow \dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{32}}{3}:\dfrac{4}{3} = 8.\)
Chọn B.
Câu 11 (VD) - Độ dài đường tròn, cung tròn
Phương pháp:
Công thức tính diện tích đường tròn bán kính \(R\) là: \(S = \pi {R^2}.\)
Cách giải:
Giả sử cho \(\Delta ABC\) đều cạnh \(a\) nội tiếp đường tròn \(\left( {O;\,\,R} \right).\)
Gọi \(M\) là trung điểm của \(BC.\)
Áp dụng định lý Pitago cho \(\Delta ABM\) vuông tại \(M\) ta có: \(\begin{array}{l}AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}.\\ \Rightarrow AO = R = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}.\\ \Rightarrow {S_{\left( O \right)}} = \pi {R^2} = \pi .{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)^2} = \dfrac{{\pi {a^2}}}{3}.\end{array}\)
Chọn D.
Câu 12 (NB) - Tỉ số lượng giác của góc nhọn
Phương pháp:
Sử dụng các công thức lượng giác của góc nhọn trong tam giác vuông.
Cách giải:
Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}\sin B = \cos C = \dfrac{{AC}}{{BC}}\\\cos B = \sin C = \dfrac{{AB}}{{BC}}\\\tan B = \cot C = \dfrac{{AC}}{{AB}}\\\cot B = \tan C = \dfrac{{AB}}{{AC}}\end{array} \right.\)
Chọn B.
PHẦN II: TỰ LUẬN (7 điểm)
Câu 1 (VD)
Phương pháp:
Sử dụng công thức \(\sqrt {{A^2}B} = \left| A \right|\sqrt B = \left\{ \begin{array}{l}A\sqrt B \,\,\,khi\,\,\,A \ge 0\\ - A\sqrt B \,\,\,khi\,\,\,A < 0\end{array} \right.;\,\,\sqrt {AB} = \sqrt A .\sqrt B \) rồi đặt nhân tử chung của tử số và rút gọn biểu thức.
Cách giải:
Rút gọn biểu thức sau: \(A = \dfrac{{4 + \sqrt 8 + \sqrt 2 - \sqrt 3 - \sqrt 6 }}{{2 + \sqrt 2 - \sqrt 3 }}.\)
\(\begin{array}{l}A = \dfrac{{4 + \sqrt 8 + \sqrt 2 - \sqrt 3 - \sqrt 6 }}{{2 + \sqrt 2 - \sqrt 3 }} = \dfrac{{4 + 2\sqrt 2 + \sqrt 2 - \sqrt 3 - \sqrt {2.3} }}{{2 + \sqrt 2 - \sqrt 3 }}\\\,\,\,\,\, = \dfrac{{4 + 3\sqrt 2 - \sqrt 3 - \sqrt {2.3} }}{{2 + \sqrt 2 - \sqrt 3 }} = \dfrac{{\left( {2 + \sqrt 2 - \sqrt 3 } \right) + \left( {2\sqrt 2 + 2 - \sqrt {2.3} } \right)}}{{2 + \sqrt 2 - \sqrt 3 }}\\\,\,\,\,\, = \dfrac{{2 + \sqrt 2 - \sqrt 3 }}{{2 + \sqrt 2 - \sqrt 3 }} + \dfrac{{\sqrt 2 \left( {2 + \sqrt 2 - \sqrt 3 } \right)}}{{2 + \sqrt 2 - \sqrt 3 }} = 1 + \sqrt 2 \end{array}\)
Vậy \(A = 1 + \sqrt 2 \).
Câu 2 (VD)
Phương pháp:
a) Giải phương trình bằng công thức nghiệm của phương trình bậc hai.
b) Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Giải phương trình ẩn \(t,\) đối chiếu với điều kiện rồi tìm ẩn \(x.\)
c) Giải hệ phương trình bằng phương pháp cộng đại số.
Cách giải:
a) \(5{x^2} + 13x - 6 = 0\)
Ta có: \(a = 5,\,\,b = 13,\,\,c = - 6.\)
\( \Rightarrow \Delta = {b^2} - 4ac = {13^2} + 4.5.6 = 289 > 0 \Rightarrow \sqrt \Delta = \sqrt {289} = 17.\)
\( \Rightarrow \) Phương trình có hai nghiệm phân biệt: \(\left[ \begin{array}{l}{x_1} = \dfrac{{ - 13 + 17}}{{2.5}} = \dfrac{4}{{10}} = \dfrac{2}{5}\\{x_2} = \dfrac{{ - 13 - 17}}{{2.5}} = \dfrac{{ - 30}}{{10}} = - 3\end{array} \right..\)
Vậy phương trình có tập nghiệm: \(S = \left\{ { - 3;\,\,\dfrac{2}{5}} \right\}.\)
b) \({x^4} + 2{x^2} - 15 = 0\)
Đặt \({x^2} = t\,\,\left( {t \ge 0} \right).\) Khi đó ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,{t^2} + 2t - 15 = 0 \Leftrightarrow {t^2} + 5t - 3t - 15 = 0\\ \Leftrightarrow t\left( {t + 5} \right) - 3\left( {t + 5} \right) = 0 \Leftrightarrow \left( {t + 5} \right)\left( {t - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}t + 5 = 0\\t - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = - 5\,\,\,\left( {ktm} \right)\\t = 3\,\,\,\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Với \(t = 3 \Rightarrow {x^2} = 3 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 3 \\x = - \sqrt 3 \end{array} \right..\)
Vậy phương trình đã cho có tập nghiệm \(S = \left\{ { - \sqrt 3 ;\,\,\,\sqrt 3 } \right\}.\)
c) \(\left\{ \begin{array}{l}3x - 4y = 17\\5x + 2y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - 4y = 17\\10x + 4y = 22\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}13x = 39\\5x + 2y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\5.3 + 2y = 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = - 2\end{array} \right.\)
Vậy hệ phương trình đã cho có nghiệm duy nhất \(\left( {x;\,\,y} \right) = \left( {3; - 2} \right).\)
Câu 3 (VD)
Phương pháp:
a) Lập bảng giá trị, vẽ đồ thị hàm số trên hệ trục tọa độ.
b) Thay tọa độ điểm \(M\left( {1; - 1} \right)\) vào phương trình đường thẳng \(\left( d \right)\) để tìm \(m.\)
Cách giải:
a) Trong mặt phẳng tọa độ \(Oxy\) vẽ parabol \(y = \dfrac{1}{2}{x^2}.\)
Ta có bảng giá trị:
|
\(x\) |
\( - 4\) |
\( - 2\) |
\(0\) |
\(2\) |
\(4\) |
|
\(y = \dfrac{1}{2}{x^2}\) |
\(8\) |
\(2\) |
\(0\) |
\(2\) |
\(8\) |
Vậy đồ thị hàm số \(y = \dfrac{1}{2}{x^2}\) là đường cong đi qua các điểm \(\left( { - 4;\,\,8} \right),\,\,\left( { - 2;\,\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {2;\,\,2} \right),\,\,\left( {4;\,\,8} \right)\) và nhận trục \(Oy\) làm trục đối xứng.
Ta có đồ thị hàm số:
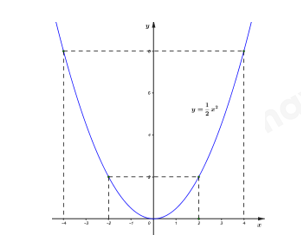
b) Tìm \(m\) để đường thẳng \(\left( d \right):\,\,\,y = \left( {m - 1} \right)x + \dfrac{1}{2}{m^2} + m\) đi qua điểm \(M\left( {1; - 1} \right).\)
Ta có điểm \(M\left( {1; - 1} \right)\) thuộc đường thẳng \(\left( d \right):\,\,\,y = \left( {m - 1} \right)x + \dfrac{1}{2}{m^2} + m\) nên thay tọa độ điểm \(M\) vào phương trình đường thẳng \(\left( d \right)\) ta được:
\(\begin{array}{l} - 1 = \left( {m - 1} \right).1 + \dfrac{1}{2}{m^2} + m \Leftrightarrow \dfrac{1}{2}{m^2} + m + m - 1 + 1 = 0\\ \Leftrightarrow \dfrac{1}{2}{m^2} + 2m = 0 \Leftrightarrow \dfrac{1}{2}m\left( {m + 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m + 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 4\end{array} \right..\end{array}\)
Vậy\(m = 0,\,\,m = - 4\) thỏa mãn bài toán.
Câu 4 (2,5 điểm) (VD):
Phương pháp:
a) Sử dụng dấu hiệu nhận biết để chứng minh tứ giác nội tiếp.
b) Chứng minh các tam giác đồng dạng rồi suy ra các tỉ lệ và đẳng thức tương ứng.
c) Góc có đỉnh nằm trong đường tròn có số đo bằng nửa tổng số đo hai cung bị chắn.
Cách giải
Cho đường tròn tâm \(\left( O \right)\) với dây \(AB\) cố định không phải đường kính. Gọi C là điểm thuộc cung lớn AB sao cho tam giác ABC nhọn. M, N lần lượt là điểm chính giữa của cung nhỏ AB và AC. Gọi I là giao điểm của BN và CM. Gọi I là giao điểm của BN và CM. Dây MN cắt AB và AC lần lượt tại H và K.
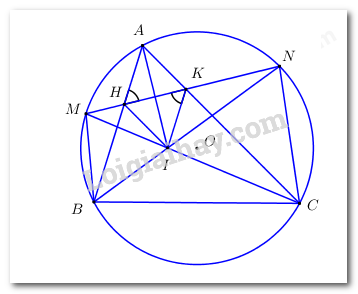
a) Chứng minh tứ giác BMHI nội tiếp.
Ta có: \(\angle ABN = \angle NMC\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
\( \Rightarrow HBI = \angle HMI \Rightarrow \) Tứ giác \(BMHI\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn 1 cạnh dưới các góc bằng nhau).
b) Chứng minh \(MK.MN = MI.MC\).
Ta có: \(\angle MNB = \angle ACM\) (trong 1 đường tròn, hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).
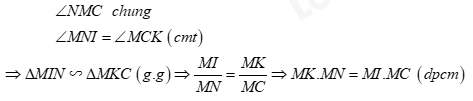
\( \Rightarrow \angle MNI = \angle MCK\).
Xét tam giác \(MIN\) và tam giác \(MKC\) có :
c) Chứng minh tam giác AKI cân tại K.
Ta có : \(\angle MNI = \angle MCK\,\,\left( {cmt} \right) \Rightarrow \) Tứ giác \(NCIK\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề cùng nhìn 1 cạnh dưới các góc bằng nhau).
\( \Rightarrow \angle HKI = \angle NCI = \angle NCM\) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp).
Ta có \(\angle NMC = \dfrac{{sdcungMN}}{2}\) (góc nội tiếp bằng nửa số đo cung bị chắn).
\(\angle AHN = \dfrac{{sdcungAN + sdcungBM}}{2} = \dfrac{{sdcungAN + sdcungAM}}{2} = \dfrac{{sdcungMN}}{2}\) (góc có đỉnh bên trong đường tròn).
\( \Rightarrow \angle NCM = \angle AHK \Rightarrow \angle HKI = \angle AHK\).
Mà 2 góc này ở vị trí 2 góc so le trong \( \Rightarrow AH//KI\).
Chứng minh hoàn toàn tương tự ta có \(\angle AKH = \angle KHI\).
Mà 2 góc này ở vị trí 2 góc so le trong \( \Rightarrow AK//HI\).
Xét tứ giác \(AHIK\) có : \(\left\{ \begin{array}{l}AH//KI\\AK//HI\end{array} \right. \Rightarrow \) Tứ giác \(AHIK\) là hình bình hành (1) (Tứ giác có các cặp cạnh đối song song).
Tứ giác \(BMHI\) là tứ giác nội tiếp \( \Rightarrow \angle MHB = \angle MIB\) (hai góc nội tiếp cùng chắn cung MB).
Tứ giác \(NCIK\) là tứ giác nội tiếp \( \Rightarrow \angle NKC = \angle KIC\) (hai góc nội tiếp cùng chắn cung NC).
Mà \(\angle MIB = \angle NIC\) (đối đỉnh) \( \Rightarrow \angle MHB = \angle NKI\).
\(\angle AHK = \angle AKH\) (do \(\angle MHB = \angle AHK;\,\,\angle NKC = \angle AKH\) đối đỉnh).
\( \Rightarrow \Delta AHK\) cân tại \(H \Rightarrow AH = AK\,\,\left( 2 \right)\).
Từ (1) và (2) \( \Rightarrow \) Tứ giác \(AHIK\) là hình thoi (Hình bình hành có 2 cạnh kề bằng nhau).
\( \Rightarrow KA = KI\) (các cạnh của hình thoi).
Vậy tam giác AKI cân tại K (đpcm).
Câu 5 (VDC):
Phương pháp :
Biến đổi biểu thức bài cho, đặt ẩn phụ, biến đổi biểu thức về dạng một bình phương công với một số rồi kết luận.
Cách giải:
Điều kiện : \(x \ne 0.\)
Ta có: \(A = \dfrac{{{x^2} - 3x + 2019}}{{{x^2}}} = 1 - \dfrac{3}{x} + \dfrac{{2019}}{{{x^2}}}\)
Đặt \(t = \dfrac{1}{x}\,\,\left( {t \ne 0} \right)\), khi đó ta có:
\(\begin{array}{l}A = 1 - 3t + 2019{t^2} = 2019\left( {{t^2} - \dfrac{1}{{673}}t} \right) + 1\\\,\,\,\,\, = 2019\left[ {{t^2} - 2t.\dfrac{1}{{1346}} + {{\left( {\dfrac{1}{{1346}}} \right)}^2}} \right] - 2019.{\left( {\dfrac{1}{{1346}}} \right)^2} + 1\\\,\,\,\,\, = 2019{\left( {t - \dfrac{1}{{1346}}} \right)^2} + \dfrac{{2689}}{{2692}}\end{array}\)
Ta có
\(\begin{array}{l}{\left( {t - \dfrac{3}{{4038}}} \right)^2} \ge 0\,\,\,\,\,\forall t \Leftrightarrow 2019{\left( {t - \dfrac{3}{{4038}}} \right)^2} \ge 0\,\,\,\,\forall t\\ \Leftrightarrow {\left( {t - \dfrac{3}{{4038}}} \right)^2} + \dfrac{{2689}}{{2692}} \ge \dfrac{{2689}}{{2692}}\,\,\,\,\forall t\\ \Rightarrow A \ge \dfrac{{2689}}{{2692}}\,\,\,\forall t\end{array}\)
Dấu "=" xảy ra \( \Leftrightarrow t = \dfrac{1}{{1346}}\,\,\,\left( {tm} \right)\).
Vậy \(\min A = \dfrac{{2689}}{{2692}}\) đạt được khi \(t = \dfrac{1}{{1346}} \Leftrightarrow x = 1346\,\,\,\left( {tm} \right).\,\,\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề thi vào 10 môn Toán Hậu Giang năm 2019 timdapan.com"