Đề thi vào 10 môn Toán Đắk Lắk năm 2023

Đề bài

Câu 1: a) Rút gọn biểu thức: \(E = 3\sqrt 5 {\rm{ \;}} - \sqrt {20} {\rm{ \;}} + \sqrt 5 \).

b) Giải phương trình: \({x^2} + 4x + 3 = 0\).

c) Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 3}\\{2x + y = 7}\end{array}} \right.\).

Câu 2: Cho biểu thức \(A = {\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right)^2} \cdot \left( {\frac{{\sqrt x {\rm{ \;}} - 1}}{{\sqrt x {\rm{ \;}} + 1}} + \frac{{\sqrt x {\rm{ \;}} + 1}}{{1 - \sqrt x }}} \right)\) với \(x > 0\) và \(x \ne 1\).

a) Rút gọn biểu thức \(A\).

b) Tìm tất cả các giá trị của \(x\) để \(A \ge 0\).

Câu 3: Cho hàm số \(y = {x^2}\) có đồ thị là đường parabol \((P)\) và hàm số \(y = 4mx + 5\) có đồ thị là đường thằng \((d)\), với \(m\) là tham số.

a) Tìm các giá trị của tham số \(m\) để đường thẳng \((d)\) và đường thẳng \((\Delta )\) song song với nhau, với \((\Delta )\) là đồ thị của hàm số \(y = (5 - m)x - 3\).

b) Tìm các giá trị của tham số \(m\) để đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thoả mãn \(x_2^2 + 4m{x_1} = 105\).

Câu 4: Một khu vườn hình chữ nhật có chiều rộng ngắn hơn chiều dài 45 m. Tính diện tích của khu vườn, biết rằng nếu chiều dài giảm 2 lần và chiều rộng tăng 3 lần thì chu vi khu vườn không thay đổi.

Câu 5: Cho nửa đường tròn tâm O đường kính AB. Gọi M là điểm chính giữa cung AB, E là điểm trên cung AM (E khác A và M). Lấy điểm F trên đoạn BE sao cho BF = AE. Gọi K là giao điểm của MO và BE.

a) Chứng minh rằng EAOK là tứ giác nội tiếp.

b) Chứng minh rằng \(\Delta EMF\) vuông cân.

c) Hai đường thẳng AE và OM cắt nhau tại D. Chứng minh rằng MK.ED = MD.EK.

Câu 6: Bút chì có dạng hình trụ, có đường kính đáy 8mm và chiều cao bằng 180mm. Thân bút chì được làm bằng gỗ, phần lõi được làm bằng thân chì. Phần lõi có dạng hình trụ có chiều cao bằng chiều dài bút và đáy là hình tròn có đường kính 2mm. Tính thể tích phần gỗ của 2024 chiếc bút chì (lấy \(\pi {\rm{ \;}} = 3,14\)).

Câu 7: Cho các số thực dương a, b, c thay đổi và thoả mãn điều kiện \(a + 9b + 6c = 2023\). Tìm giá trị lớn nhất của biểu thức:

\(P = \sqrt {3{a^2} + 63ab + 243{b^2}} {\rm{ \;}} + \sqrt {243{b^2} + 378bc + 108{c^2}} {\rm{ \;}} + \sqrt {108{c^2} + 42ca + 3{a^2}} \).

----- HẾT -----

---

Lời giải chi tiết

Câu 1 (VD):

Phương pháp:

1. Sử dụng căn bậc hai: \(\sqrt {{A^2}} \; = |A|\), nhóm hạng tử.

2. Bước 1: Tính giá trính của \(\Delta \) với \(\Delta \; = {{\rm{b}}^2} - 4{\rm{ac}}\)

Bước 2: Xét tập nghiệm của phương trình bằng việc sánh giá \(\Delta \) với 0

\(\Delta \; < 0 = \; > \) phương trình bậc 2 vô nghiệm

\(\Delta \; = 0 = \; > \) phương trình bậc 2 có nghiệm kép \({x_1} = {x_2} = \; - \frac{b}{{2a}}\)

\(\Delta \; > 0 = \; > \) phương trình (1) có 2 nghiệm phân biệt, ta dùng công thức nghiệm sau: \({x_{1,2}} = \frac{{ - b \pm \sqrt \Delta  {\rm{ \;}}}}{{2a}}\)

3. Sử dụng phương pháp thế hoặc trừ vế.

Cách giải:

a) Rút gọn biểu thức: \(E = 3\sqrt 5  - \sqrt {20}  + \sqrt 5 \).

\(\begin{array}{l}E = 3\sqrt 5  - \sqrt {20}  + \sqrt 5 \\ = 3\sqrt 5  - \sqrt {4.5}  + \sqrt 5 \\ = 3\sqrt 5  - 2\sqrt 5  + \sqrt 5 \\ = \left( {3 - 2 + 1} \right)\sqrt 5  = 2\sqrt 5 .\end{array}\)

Vậy \(E = 2\sqrt 5 \).

b) Giải phương trình: \({x^2} + 4x + 3 = 0\).

Xét phương trình \({x^2} + 4x + 3 = 0\) có \(a - b + c = 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} =  - 1\\{x_2} =  - \frac{c}{a} =  - 3\end{array} \right.\).

Vậy phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} =  - 1\\{x_2} =  - 3\end{array} \right.\).

c) Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{3x - y = 3}\\{2x + y = 7}\end{array}} \right.\).

Cộng vế với vế ta có \(\left\{ {\begin{array}{*{20}{l}}{5x = 10}\\{2x + y = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{2x + y = 7}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;3} \right).\)

Câu 2 (VD):

Phương pháp:

1. Quy đồng và rút gọn.

2. Giải phương trình \(A \ge 0\).

Cách giải:

a) Rút gọn biểu thức \(A\).

Với \(x > 0\) và \(x \ne 1\) ta có:

\(\begin{array}{l}A = {\left( {\frac{{\sqrt x }}{2} - \frac{1}{{2\sqrt x }}} \right)^2} \cdot \left( {\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} + \frac{{\sqrt x  + 1}}{{1 - \sqrt x }}} \right)\\ = {\left( {\frac{x}{{2\sqrt x }} - \frac{1}{{2\sqrt x }}} \right)^2} \cdot \left( {\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} - \frac{{\sqrt x  + 1}}{{\sqrt x  - 1}}} \right)\end{array}\)

\(\begin{array}{l}\, = {\left( {\frac{{x - 1}}{{2\sqrt x }}} \right)^2} \cdot \frac{{{{\left( {\sqrt x  - 1} \right)}^2} - {{\left( {\sqrt x  + 1} \right)}^2}}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\\,\,\,\, = \frac{{{{\left( {x - 1} \right)}^2}}}{{4x}} \cdot \frac{{x - 2\sqrt x  + 1 - x - 2\sqrt x  - 1}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\\,\,\,\, = \frac{{{{\left( {x - 1} \right)}^2}}}{{4x}} \cdot \frac{{ - 4\sqrt x }}{{x - 1}}\\\,\,\,\, = \frac{{1 - x}}{{\sqrt x }}\end{array}\)

Vậy \(A = \frac{{1 - x}}{{\sqrt x }}\).

b) Tìm tất cả các giá trị của \(x\) để \(A \ge 0\).

Ta có: \(A \ge 0 \Leftrightarrow \frac{{1 - x}}{{\sqrt x }} \ge 0\)

Vì \(\sqrt x  > 0\)nên \(\frac{{1 - x}}{{\sqrt x }} \ge 0 \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\)

Kết hợp với điều kiện \(x > 0\) và \(x \ne 1\) ta có: \(0 < x < 1\)

Vậy \(0 < x < 1\).

Câu 3 (VD):

Cách giải:

a) Tìm các giá trị của tham số \(m\) để đường thẳng \((d)\) và đường thẳng \((\Delta )\) song song với nhau, với \((\Delta )\) là đồ thị của hàm số \(y = (5 - m)x - 3\).

Để đường thẳng \((d)\) và đường thẳng \((\Delta )\) song song với nhau thì

\(\left\{ \begin{array}{l}5 - m = 4m\\ - 3 \ne 5\end{array} \right. \Leftrightarrow 5 - m = 4m \Leftrightarrow 5m = 5 \Leftrightarrow m = 1\)

Vậy với \(m = 1\) thì đường thẳng \((d)\) và đường thẳng \((\Delta )\) song song với nhau.

b) Tìm các giá trị của tham số \(m\) để đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thoả mãn \(x_2^2 + 4m{x_1} = 105\).

Xét phương trình hoành độ giao điểm của (d) và (P) là  \({x^2} = 4mx + 5 \Leftrightarrow {x^2} - 4mx - 5 = 0\)  (1)

Do \(a.c =  - 5 < 0\) nên phương trình (1) luôn có 2 nghiệm trái dấu \({x_1},{x_2}\)  hay (d) luôn cắt (P) tại 2 điểm phân biệt với mọi m 

Áp dụng hệ thức Viet ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 4m\\{x_1}{x_2} =  - 5\end{array} \right.\)

Do \({x_2}\) là nghiệm của (1) nên \(x_2^2 - 4m{x_2} - 5 = 0 \Leftrightarrow x_2^2 = 4m{x_2} + 5\)

Để \(x_2^2 + 4m{x_1} = 105\)

\(\begin{array}{l} \Leftrightarrow 4m{x_2} + 5 + 4m{x_1} = 105\\ \Leftrightarrow 4m\left( {{x_1} + {x_2}} \right) = 100\\ \Leftrightarrow 4m.4m = 100\\ \Leftrightarrow {m^2} = \frac{{25}}{4}\\ \Leftrightarrow \left[ \begin{array}{l}m = \frac{5}{2}\\m =  - \frac{5}{2}\end{array} \right.\left( {TM} \right)\end{array}\)

Vậy với \(m =  \pm \frac{5}{2}\) thì đường thẳng \((d)\) cắt parabol \((P)\) tại hai điểm phân biệt có hoành độ \({x_1},{x_2}\) thoả mãn \(x_2^2 + 4m{x_1} = 105\).

Câu 4 (VD):

Phương pháp:

Giải bài toán bằng cách lập phương trình.

Cách giải:

Gọi chiều dài khu vườn là \(x\)  (\(x > 45\), mét)

Vì chiều rộng ngắn hơn chiều dài 45 m nên chiều rộng khu vườn là \(x - 45\) (m)

Chu vi khu vườn là: \(2.\left( {x + x - 45} \right) = 2\left( {2x - 45} \right)\)

Chiều dài khu vườn khi giảm đi  2 lần là \(\frac{x}{2}\) (m)

Chiều rộng khu vườn khi tăng lên 3 lần là \(3\left( {x - 45} \right)\) (m)

Khi đó chu vi khu vườn là: \(2\left( {\frac{x}{2} + 3\left( {x - 45} \right)} \right) = 2\left( {\frac{7}{2}x - 135} \right)\)

Vì chu vi khu vườn không đổi nên ta có phương trình: \(2.\left( {2x - 45} \right) = 2.\left( {\frac{7}{2}x - 135} \right)\)

\(\begin{array}{l} \Leftrightarrow 2x - 45 = \frac{7}{2}x - 135\\ \Leftrightarrow \frac{3}{2}x = 90\\ \Leftrightarrow x = 60\,\,(TM)\end{array}\)

Suy ra chiều dài khu vườn là 60m, chiều rộng khu vườn là \(60 - 45 = 15\) (m)

Diện tích khu vườn là: \(60.15 = 900\left( {{m^2}} \right)\)

Vậy diện tích khu vườn là: \(900{m^2}.\)

Câu 5 (VD):

Cách giải:

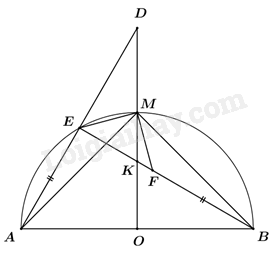
a) Chứng minh rằng EAOK là tứ giác nội tiếp.

Vì M là điểm chính giữa của cung AB nên \(OM \bot AB\) \( \Rightarrow \angle AOK = {90^0}\).

Ta có \(\angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \angle AEK = {90^0}\).

Xét tứ giác EAOK có: \(\angle AOK + \angle AEK = {90^0} + {90^0} = {180^0}\).

Mà E, O là hai đỉnh đối diện của tứ giác EAOK.

=> EAOK là tứ giác nội tiếp (dhnb) (đpcm).

b) Chứng minh rằng \(\Delta EMF\) vuông cân.

Nối AM, FM.

Vì M là điểm chính giữa cung AB nên số đo cung AM = số đo cung BM

=> AM = BM (hai dây căng hai cung bằng nhau thì bằng nhau).

Xét \(\Delta AEM\) và \(\Delta FBM\) có:

\(AE = BF\,\,\left( {gt} \right)\)

\(\angle EAM = \angle FBM\) (hai góc nội tiếp cùng chắn cung EM).

\(AM = BM\,\,\left( {cmt} \right)\)

\( \Rightarrow \Delta AEM = \Delta FBM\,\,\left( {c.g.c} \right)\)

\( \Rightarrow \angle AME = \angle BMF\) (hai góc tương ứng).

Ta có:

\(\angle AMB = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\(\begin{array}{l} \Rightarrow \angle AMF + \angle BMF = {90^0}\\ \Rightarrow \angle AMF + \angle AME = {90^0}\\ \Rightarrow \angle EMF = {90^0}\end{array}\)

\( \Rightarrow \Delta EMF\) vuông tại M.

Mà \(\angle MEF = \angle MEB = \frac{1}{2}\angle MOB = \frac{1}{2}{.90^0} = {45^0}\) (góc nội tiếp và góc ở tâm cùng chắn cung BM).

\( \Rightarrow \Delta EMF\) vuông cân tại M (dhnb) (đpcm).

c) Hai đường thẳng AE và OM cắt nhau tại D. Chứng minh rằng MK.ED = MD.EK.

Dễ thấy tứ giác AEMB nội tiếp (O) \( \Rightarrow \angle DEM = \angle ABM\) (góc ngoài và góc trong tại đỉnh đối diện).

Mà tam giác MAB có: \(\left\{ \begin{array}{l}\angle AMB = {90^0}\,\,\left( {cmt} \right)\\AM = BM\,\,\left( {cmt} \right)\end{array} \right.\) \( \Rightarrow \Delta AMB\) vuông cân tại M \( \Rightarrow \angle ABM = {45^0}\).

\( \Rightarrow \angle DEM = {45^0} = \angle MEF = \frac{1}{2}\angle DEK\).

\( \Rightarrow EM\) là phân giác trong của góc DEK.

Áp dụng định lí đường phân giác ta có: \(\frac{{MD}}{{MK}} = \frac{{ED}}{{EK}} \Rightarrow MK.ED = MD.EK\,\,\left( {dpcm} \right)\).

Câu 6 (VD):

Phương pháp:

Thể tích hình trụ \(V = \pi .{r_1}^2.h\)

Cách giải:

Bút chì có đường kính đáy 8mm nên bán kính đáy bằng 4mm.

Thể tích của cả cái bút chì (gồm cả phần lõi) là:

\({V_1} = \pi .{r_1}^2.h = 3,{14.4^2}.180 = 9043,2\left( {m{m^3}} \right)\)

Lõi bút chì có đường kính đáy 2mm nên bán kính đáy bằng 1mm.

Thể tích phần lõi bút là:

\({V_2} = \pi .{r_2}^2.h = 3,{14.1^2}.180 = 565,2\left( {m{m^3}} \right)\)

Tính thể tích phần gỗ của một chiếc bút chì là:

\(V = {V_1} - {V_2} = 9043,2 - 565,2 = 8478\left( {m{m^3}} \right)\)

Tính thể tích phần gỗ của 2024 chiếc bút chì là: \(2024.8478 = 17\,159\,472\left( {m{m^3}} \right)\).

Vậy thể tích phần gỗ của 2024 chiếc bút chì là: \(17\,159\,472\left( {m{m^3}} \right)\)

Câu 7 (VDC):

Cách giải:

Đặt \(x = a;y = 9b;z = 6c\); \(x,y,z > 0\)

Suy ra: \(x + y + z \le 2023\)

Khi đó: \(P = \sqrt {3{x^2} + 7xy + 3{y^2}}  + \sqrt {3{y^2} + 7yz + 3{z^2}}  + \sqrt {3{z^2} + 7zx + 3{x^2}} \)

\( = \sqrt {5{{\left( {x + y} \right)}^2} - 2{{\left( {x - y} \right)}^2}}  + \sqrt {5{{\left( {y + z} \right)}^2} - 2{{\left( {y - z} \right)}^2}}  + \sqrt {5{{\left( {z + x} \right)}^2} - 2{{\left( {z - x} \right)}^2}} \)

Vì \({\left( {x - y} \right)^2} \ge 0\); \({\left( {y - z} \right)^2} \ge 0\); \({\left( {z - x} \right)^2} \ge 0\) nên ta có:

\(\begin{array}{l}P \le \sqrt {5{{\left( {x + y} \right)}^2}}  + \sqrt {5{{\left( {y + z} \right)}^2}}  + \sqrt {5{{\left( {z + x} \right)}^2}} \\\,\,\,\, = \sqrt 5 \left( {x + y} \right) + \sqrt 5 \left( {y + z} \right) + \sqrt 5 \left( {z + x} \right)\\\,\,\,\, = 2\sqrt 5 \left( {x + y + z} \right) \le 2\sqrt 5 .2023 = 4046\sqrt 5 \end{array}\)

Dấu “=” xảy ra khi và chỉ khi \(x = y = z\) hay \(a = 9b = 6c = \frac{{2023}}{3}\)

Vậy giá trị lớn nhất của P là \(4046\sqrt 5 \) khi \(a = 9b = 6c = \frac{{2023}}{3}\).