Đề thi vào 10 môn Toán Bình Thuận năm 2021

Bài 1 (2,0 điểm): Giải phương trình và hệ phương trình sau:

Đề bài

Bài 1 (2,0 điểm): Giải phương trình và hệ phương trình sau:

a) \({x^2} + 3x - 4 = 0\) b) \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = - 4\end{array} \right.\)

Bài 2 (2,0 điểm): Rút gọn các biểu thức sau:

a) \(A = \left( {\sqrt {27} + 3\sqrt {12} - 2\sqrt 3 } \right):\sqrt 3 \) b) \(B = \left( {\frac{1}{{\sqrt x + 3}} + \frac{5}{{\sqrt x - 3}} + \frac{6}{{x - 9}}} \right):\frac{2}{{\sqrt x - 3}}\) với \(x \ge 0\) và \(x \ne 9\)

Bài 3 (1,5 điểm): Cho hàm số \(y = 2{x^2}\) có đồ thị \(\left( P \right)\)

a) Vẽ đồ thị \(\left( P \right)\) trên mặt phẳng tọa độ \(\left( {Oxy} \right)\)

b) Tìm tất cả các giá trị của tham số \(m\) để đường thẳng \(\left( d \right):y = 2mx + 1\) cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ là \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\) và \(\left| {{x_2}} \right| - \left| {{x_1}} \right| = 2021\).

Bài 4 (1,0 điểm): Một phân xưởng theo kế hoạch phải may \(1200\) bộ quần áo trong một thời gian quy định. Khi thực hiện, do cải tiến kỹ thuật nên mỗi ngày phân xưởng may thêm được \(10\) bộ quần áo và hoàn thành kế hoạch trước 4 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng may bao nhiêu bộ quần áo?

Bài 5 (1,0 điểm): Một cốc nước dạng hình trụ có chiều cao là \(15cm\), bán kính đáy là \(3cm\) và lượng nước ban đầu trong cốc cao \(10cm\). Thả chìm hoàn toàn vào cốc nước \(5\) viên bi thủy tinh hình cầu có cùng bán kính là \(1cm\). Hỏi sau khi thả \(5\) viên bi, mực nước trong cốc cách miệng cốc một khoảng bằng bao nhiêu?

(Giả sử độ dày của thành cốc và đáy cốc không đáng kể; kết quả làm tròn đến chứ số thập phân thứ hai).

Bài 6 (2,5 điểm) Từ điểm \(A\) nằm bên ngoài đường tròn \(\left( O \right)\) vẽ các tiếp tuyến \(AB,\,\,AC\) với đường tròn \(\left( O \right)\) (\(B,\,\,C\) là các tiếp điểm).

a) Chứng minh tứ giác \(ABOC\) nội tiếp.

b) Từ \(A\) vẽ cát tuyến \(AEF\) đến đường tròn \(\left( O \right)\) (với \(AE < AF\)). Chứng minh \(A{C^2} = AE.AF\).

c) \(OA\) cắt \(BC\) tại \(H\). Gọi \(M\) là trung điểm của đoạn thẳng \(HB\), tia \(OM\) cắt \(AB\) tại \(K\). Đặt \(\angle AOB = \alpha \). Chứng minh \({\cos ^2}\alpha = \frac{{KB}}{{KA}}\).

Bài 7 (0,5 điểm) Ba bạn Đào, Mai, Trúc mặc ba chiếc áo màu trắng, hồng, xanh và đeo ba cái khẩu trang cũng màu trắng, hồng, xanh. Biết rằng:

a) Trúc đeo khẩu trang màu xanh.

b) Chỉ có bạn Đào là có màu áo và màu khẩu trang giống nhau.

c) Màu áo và màu khẩu trang của bạn Mai đều không phải màu trắng.

Dựa vào các thông tin trên, em hãy cho biết mỗi bạn Đào, Mai, Trúc mặc áo màu gì và đeo khẩu trang màu gì?

Lời giải

Bài 1:

Phương pháp:

a) Sử dụng chú ý để giải phương trình bậc hai một ẩn \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) nếu có \(a + b + c = 0\) thì phương trình có hai nghiệm phân biệt \({x_1} = 1;{x_2} = \frac{c}{a}\).

b) Vận dụng phương pháp cộng đại số để tìm nghiệm của hệ phương trình

Cách giải

a) \({x^2} + 3x - 4 = 0\)

Ta có \( + b + c = 1 + 3 - 4 = 0\) nên phương trình có hai nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} = 1\\{x_2} = \frac{c}{a} = - 4\end{array} \right.\).

Vậy tập nghiệm của phương trình là \(S = \left\{ {1; - 4} \right\}\).

b) Ta có: \(\left\{ \begin{array}{l}x + 2y = 4\\x - 2y = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4y = 8\\x = 4 - 2y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 2\\x = 0\end{array} \right.\).

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {0;2} \right)\).

Bài 2:

Phương pháp:

a) Vận dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Thực hiện các phép với căn bậc hai

b) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a - \sqrt b } \right)\left( {\sqrt a + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức

Thực hiện các phép toán với các phân thức đại số để rút gọn biểu thức \(B\)

Cách giải:

a) \(A = \left( {\sqrt {27} + 3\sqrt {12} - 2\sqrt 3 } \right):\sqrt 3 \)

Ta có:

\(\begin{array}{l}A = \left( {\sqrt {27} + 3\sqrt {12} - 2\sqrt 3 } \right):\sqrt 3 \\\,\,\,\, = \left( {\sqrt {9.3} + 3\sqrt {3.4} - 2\sqrt 3 } \right):\sqrt 3 \\\,\,\,\,\, = \left( {3\sqrt 3 + 6\sqrt 3 - 2\sqrt 3 } \right):\sqrt 3 \\\,\,\,\,\, = 7\sqrt 3 :\sqrt 3 = 7\end{array}\)

Vậy \(A = 7\).

b) Với \(x \ge 0\) và \(x \ne 9\) ta có:

\(\begin{array}{l}B = \left( {\frac{1}{{\sqrt x + 3}} + \frac{5}{{\sqrt x - 3}} + \frac{6}{{x - 9}}} \right):\frac{2}{{\sqrt x - 3}}\\\,\,\,\, = \frac{{\sqrt x - 3 + 5\left( {\sqrt x + 3} \right) + 6}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}:\frac{2}{{\sqrt x - 3}}\\\,\,\,\, = \frac{{6\sqrt x + 18}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}.\frac{{\sqrt x - 3}}{2}\\\,\,\,\, = \frac{{6\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 3} \right)}}.\frac{{\sqrt x - 3}}{2}\\\,\,\,\, = 3\end{array}\)

Vậy với \(x \ge 0\) và \(x \ne 9\) thì \(B = 3\).

Bài 3

Phương pháp:

a) Nhận xét tính đồng biến, nghịch biến của hàm số \(y = 2{x^2}\)

Lập bằng giá trị tương ứng của \(x\) và \(y\), sau đó vẽ đồ thị.

b) Xét phương trình hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol

Giả sử hai nghiệm đó là \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\), sau đó theo hệ thức Vi – ét, tính được \({x_1} + {x_2};{x_1}.{x_2}\)

Lập luận và thay vào hệ thức của đề bài để tìm giá trị của \(m\).

Cách giải:

a) Hàm số có hệ số \(a = 2 > 0\) nên đồng biến với \(x > 0\) và nghịch biến với \(x < 0\).

Đồ thị hàm số đi qua gốc tọa độ \(O\left( {0;0} \right)\) và nhận \(Oy\) làm trục đối xứng.

Bảng giá trị:

\(x\)	\( - \frac{3}{2}\)	\( - 1\)	\(0\)	\(1\)	\(\frac{3}{2}\)
\(y = 2{x^2}\)	\(\frac{9}{2}\)	\(2\)	\(0\)	\(2\)	\(\frac{9}{2}\)

\( \Rightarrow \) Parabol \(y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - \frac{3}{2};\frac{9}{2}} \right);\,\,\left( { - 1;2} \right);\,\,\left( {0;0} \right);\,\,\left( {1;2} \right);\,\,\left( {\frac{3}{2};\frac{9}{2}} \right)\).

Đồ thị hàm số:

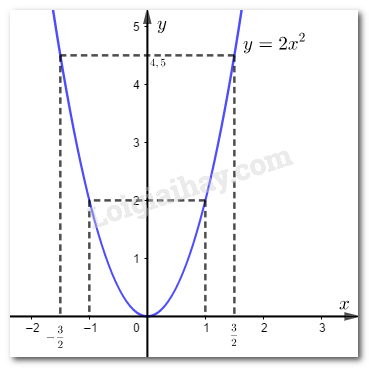
b) Hoành độ giao điểm của đường thẳng \(\left( d \right)\) và Parabol \(\left( P \right)\) là nghiệm của phương trình:

\(2{x^2} = 2mx + 1 \Leftrightarrow 2{x^2} - 2mx - 1 = 0\)

Ta có: \(\Delta ' = {\left( { - m} \right)^2} - 2.\left( { - 1} \right) = {m^2} + 2 > 0\) với mọi \(m \in \mathbb{R}\).

Suy ra đường thẳng \(\left( d \right)\) luôn cắt Parabol \(\left( P \right)\) tại hai điểm phân biệt.

Giả sử hai nghiệm đó là \({x_1},{x_2}\) thỏa mãn \({x_1} < {x_2}\).

Theo định lí Vi-et, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = m\\{x_1}{x_2} = \frac{{ - 1}}{2}\end{array} \right.\).

Vì tích \({x_1}{x_2} = \frac{{ - 1}}{2} < 0\) và \({x_1} < {x_2}\) nên \({x_1} < 0,{x_2} > 0\). Do đó ta có:

\(\left| {{x_2}} \right| - \left| {{x_1}} \right| = 2021 \Leftrightarrow {x_2} - \left( { - {x_1}} \right) = 2021 \Leftrightarrow {x_1} + {x_2} = 2021 \Rightarrow m = 2021\)

Vậy \(m = 2021\) là giá trị cần tìm.

Bài 4:

Phương pháp:

Giải bài toán bằng cách lập phương trình, cụ thể gọi \(x\) là số bộ quần áo phân xưởng may trong một ngày theo kế hoạch \(\left( {x \in \mathbb{N}*} \right)\), từ đó tính được số bộ quần áo may trong một ngày trong thực tế và thời gian tương ứng của thời gian may theo kế hoạch, thời gian may thực tế.

Vì phân xưởng hoàn thành kế hoạch trước 4 ngày nên lập được phương trình.

Giải phương trình, đối chiếu điều kiện và kết luận.

Cách giải:

Gọi \(x\) là số bộ quần áo phân xưởng may trong một ngày theo kế hoạch \(\left( {x \in \mathbb{N}*} \right)\).

Số bộ quần áo may trong một ngày trong thực tế là \(x + 10\) (bộ).

Thời gian may theo kế hoạch là \(\frac{{1200}}{x}\) ngày.

Thời gian may thực tế là \(\frac{{1200}}{{x + 10}}\) ngày.

Vì phân xưởng hoàn thành kế hoạch trước 4 ngày nên ta có phương trình: \(\frac{{1200}}{x} - \frac{{1200}}{{x + 10}} = 4\)

\(\begin{array}{l} \Leftrightarrow \frac{{1200.\left( {x + 10 - x} \right)}}{{x\left( {x + 10} \right)}} = \frac{{4x\left( {x + 10} \right)}}{{x\left( {x + 10} \right)}}\\ \Leftrightarrow \frac{{1200.10}}{{x\left( {x + 10} \right)}} = \frac{{4x\left( {x + 10} \right)}}{{x\left( {x + 10} \right)}}\\ \Rightarrow x\left( {x + 10} \right) = 3000\\ \Leftrightarrow {x^2} + 10x - 3000 = 0\,\,\left( 1 \right)\end{array}\)

Ta có: \(\Delta ' = {5^2} + 3000 = 3025 = {55^2} > 0\) nên phương trình (1) có 2 nghiệm phân biệt:

\(\left[ \begin{array}{l}{x_1} = \frac{{ - 5 + 55}}{1} = 50\,\,\,\,\,\,\left( {tm} \right)\\{x_2} = \frac{{ - 5 - 55}}{1} = - 60\,\,\left( {ktm} \right)\end{array} \right.\)

Vậy theo kế hoạch mỗi ngày phân xưởng may 50 bộ quần áo.

Bài 5:

Phương pháp:

Vận dụng công thức tính thể tích hình cầu để tính thể tích của một viên bi: \(V = \frac{4}{3}\pi {r^3}\)

Tính được mực nước dâng lên \( \to \) Tính được chiều cao của lượng nước dâng lên \( \to \) Tính được chiều cao của nước sau khi thả 5 viên bi vào cốc \( \to \) Tính được mực nước cách miệng cốc bao nhiêu cm.

Cách giải:

Thể tích của bi là \({V_{bi}} = 5.\frac{4}{3}\pi {r_{bi}}^3 = 5.\frac{4}{3}\pi .1 = \frac{{20}}{3}\pi \,\,\left( {c{m^3}} \right)\)

Mặt khác thể tích của bi bằng thể tích của nước dâng nên ta có:

\(\frac{{20}}{3}\pi = \pi {.3^2}.h \Rightarrow h = \frac{{20}}{{27}}\,\,\left( {cm} \right)\) (\(h\) là chiều cao lượng nước dâng lên).

Chiều cao của nước sau khi thả 5 viên bi vào trong cốc là \(10 + \frac{{20}}{{27}} = \frac{{290}}{{27}}\,\,\left( {cm} \right)\)

Mực nước cách miệng cốc một khoảng là \(15 - \frac{{290}}{{27}} = \frac{{115}}{{27}} \approx 4,26\,\,\left( {cm} \right)\)

Vậy mực nước trong cốc cách miệng cốc là \(4,26\) cm.

Bài 6

Phương pháp:

a) Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

b) Chứng minh \(\Delta AEC \sim \Delta ACF\,\,\left( {g.g} \right)\)\( \Rightarrow A{C^2} = AE.AF\)

c) Gọi \(N\) là trung điểm của \(AH\).

Kẻ đường thẳng vuông góc với \(AB\) cắt \(BN\) tại \(P\).

Chứng minh \(\Delta BAH \sim \Delta OBH\,\,\left( {g.g} \right)\) suy ra được \(\frac{{BA}}{{AN}} = \frac{{OB}}{{BM}}\)

Chứng minh \(\Delta BAN \sim \Delta OBM\,\,\left( {c.g.c} \right);\Delta BAP \sim \Delta OBK\,\,\left( {g.g} \right)\) suy ra được \(\frac{{BK}}{{AB}} = \frac{{AP.OB}}{{A{B^2}}}\)\( \Rightarrow \frac{{BK}}{{AB}} = \frac{{AN.O{B^2}}}{{NO.A{B^2}}}\)

Vận dụng hệ thức lương trong tam giác vuông

Cách giải:

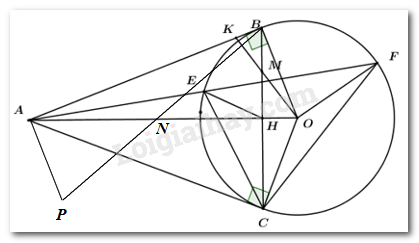
a) Vì \(AB,\,\,AC\) là các tiếp tuyến của \(\left( O \right)\) lần lượt tại \(A,\,\,B\) nên \(\angle OBA = \angle OCA = {90^0}\).

Xét tứ giác \(ABOC\) có: \(\angle ABO + \angle ACO = {180^0}\), suy ra tứ giác \(ABOC\) nội tiếp (dhnb).

b) Xét tam giác \(AEC\) và tam giác \(ACF\) có: \(\angle EAC = \angle FAC;\) \(\angle ACE = \angle CFA\) (góc nội tiếp và góc tạp bởi tiếp tuyến và dây cùng cùng chắn cung \(CE\)).

\( \Rightarrow \Delta AEC \sim \Delta ACF\,\,\left( {g.g} \right)\) \( \Rightarrow \frac{{AE}}{{AC}} = \frac{{AC}}{{FA}}\) (2 cạnh tương ứng).

\( \Rightarrow A{C^2} = AE.AF\) (đpcm).

c) Gọi \(N\) là trung điểm của \(AH\).

Kẻ đường thẳng vuông góc với \(AB\) cắt \(BN\) tại \(P\).

Xét \(\Delta BAH\) và \(\Delta OBH\) có:

\(\angle BHA = \angle OHB = {90^0}\);

\(\angle ABH = \angle BOH\) (cùng phụ với \(\angle OBH\))

\( \Rightarrow \Delta BAH \sim \Delta OBH\,\,\left( {g.g} \right)\)

\( \Rightarrow \frac{{BA}}{{AH}} = \frac{{OB}}{{BH}} \Rightarrow \frac{{BA}}{{2AN}} = \frac{{OB}}{{2BM}} \Rightarrow \frac{{BA}}{{AN}} = \frac{{OB}}{{BM}}\).

Xét \(\Delta BAN\) và \(\Delta OBM\) có: \(\frac{{BA}}{{AN}} = \frac{{OB}}{{BM}}\,\,\left( {cmt} \right)\), \(\angle BAN = \angle OBM\) (cùng phụ với \(\angle BOA\)).

\( \Rightarrow \Delta BAN \sim \Delta OBM\,\,\left( {c.g.c} \right)\) \( \Rightarrow \angle ABN = \angle BOM\) (2 cạnh tương ứng)

\(\begin{array}{l} \Rightarrow \Delta BAP \sim \Delta OBK\,\,\left( {g.g} \right)\\ \Rightarrow \frac{{AB}}{{OB}} = \frac{{AP}}{{BK}} \Rightarrow BK.AB = AP.OB \Rightarrow \frac{{BK}}{{AB}} = \frac{{AP.OB}}{{A{B^2}}}\end{array}\).

Vì \(AP//OB \Rightarrow \frac{{AP}}{{OB}} = \frac{{AN}}{{NO}}\) (định lí Ta-lét) \( \Rightarrow AP.OB = \frac{{AN}}{{NO}}.O{B^2}\)

\( \Rightarrow \frac{{BK}}{{AB}} = \frac{{AN.O{B^2}}}{{NO.A{B^2}}}\).

Lại có \(O{B^2} = OH.OA,\,\,A{B^2} = AH.AO\) (hệ thức lượng trong tam giác vuông)

\( \Rightarrow \frac{{BK}}{{AB}} = \frac{{AN.OH}}{{NO.AH}} = \frac{{\frac{1}{2}AH.OH}}{{NO.AH}} = \frac{{OH}}{{2NO}}\).

\( \Rightarrow \frac{{AB}}{{BK}} = \frac{{2NO}}{{OH}} \Rightarrow \frac{{AB - BK}}{{BK}} = \frac{{2NO - OH}}{{OH}}\)

\(\begin{array}{l} \Rightarrow \frac{{AK}}{{BK}} = \frac{{2\left( {NH + OH} \right) - OH}}{{OH}} = \frac{{2NH + OH}}{{OH}}\\ \Rightarrow \frac{{AK}}{{BK}} = \frac{{AH + OH}}{{OH}} = \frac{{AO}}{{OH}}\\ \Rightarrow \frac{{KB}}{{KA}} = \frac{{OH}}{{OA}}\end{array}\)

Lại có \(\frac{{OH}}{{OA}} = \frac{{OH.OA}}{{O{A^2}}} = \frac{{O{B^2}}}{{O{A^2}}} = {\cos ^2}\alpha \).

Vậy \(\frac{{KB}}{{KA}} = {\cos ^2}\alpha \) (đpcm).

Bài 7

Phương pháp:

Lập luận, giải thích từng trường hợp để có được kết luận.

Cách giải:

Vì chỉ có bạn Đào là có màu áo và màu khẩu trang giống nhau nên bạn Trúc đeo khẩu trang khác màu áo.

\( \Rightarrow \) Trúc mặc áo màu trắng hoặc hồng.

+) Nếu Trúc mặc áo màu hồng thì Mai mặc áo màu xanh (do Màu áo và màu khẩu trang của bạn Mai đều không phải màu trắng) và đeo khẩu trang màu hồng.

\( \Rightarrow \) Đào mặc áo trắng và đeo khẩu trang màu trắng.

+) Nếu Trúc mặc áo màu trắng \( \Rightarrow \) Đào mặc áo và đeo khẩu trang màu hồng.

\( \Rightarrow \) Mai mặc áo xanh và đeo khẩu trang màu trắng (vô lí).