Đề thi học kì 2 môn toán lớp 8 năm 2019 - 2020 trường THCS Bình Thọ

Đề bài

Bài 1 (3 điểm):

Giải các phương trình sau:

a) \(7x - 8 = 5x\)

b) \(\left( {3x + 1} \right)\left( {x - 7} \right) = 0\)

c) \(\dfrac{{x - 3}}{5} - \dfrac{{7x + 1}}{3} = \dfrac{{2x - 5}}{{15}}\) 

Bài 2 (1 điểm):

Giải bất phương trình: \(13x - 7 \le 24x + 15\)  

Bài 3 (2 điểm):

Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng là \(15m\). Nếu tăng chiều rộng \(5m\) và giảm chiều dài \(3m\) thì diện tích miếng đất tăng \(80{m^2}\). Tính kích thước miếng đất hình chữ nhật lúc đầu.

Bài 4 (1 điểm):

Sau khi xem bảng giá, mẹ bạn Lan đưa \(350\,\,000\) đồng nhờ An mua một cái bàn ủi và một bộ lau nhà. Hôm nay đúng đợt khuyến mãi, bàn ủi giảm \(10\% \), bộ lau nhà giảm \(20\% \) nên Lan chỉ phải trả \(300\,\,000\) đồng. Hỏi giá tiền một cái bàn ủi, một bộ lau nhà khi chưa giảm giá là bao nhiêu?

Bài 5 (3 điểm):

Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB < AC} \right)\). Kẻ đường cao \(AH\left( {H \in BC} \right)\).

a) Chứng minh \(\Delta BHA\) đồng dạng với \(\Delta BAC\).

b) Chứng minh \(A{H^2} = HB.HC\). 

c) Vẽ \(HM\) vuông góc với \(AC\) tại \(M\). Qua \(A\) vẽ đường thẳng song song với \(BC\) cắt đường thẳng \(HM\) tại \(I\), vẽ \(IN\) vuông góc với \(BC\) tại \(N\). Chứng minh rằng \(HM.IC = HC.MN\).

HẾT

LG bài 1

Phương pháp giải:

a) Chuyển vế đưa về giải phương trình bậc nhất một ẩn \(ax + b = 0\left( {a \ne 0} \right)\) \( \Leftrightarrow x =  - \dfrac{b}{a}\)

b) Giải phương trình tích \(A\left( x \right).B\left( x \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}A\left( x \right) = 0\\B\left( x \right) = 0\end{array} \right.\)

c) Qui đồng, bỏ mẫu rồi đưa về giải phương trình bậc nhất một ẩn

Lời giải chi tiết:

a) \(7x - 8 = 5x\)

\(\begin{array}{l} \Leftrightarrow 7x - 5x = 8\\ \Leftrightarrow 2x = 8\\ \Leftrightarrow x = 8:2\\ \Leftrightarrow x = 4\end{array}\)

Vậy phương trình có nghiệm \(x = 4.\)

b) \(\left( {3x + 1} \right)\left( {x - 7} \right) = 0\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}3x + 1 = 0\\x - 7 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3x =  - 1\\x = 7\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{1}{3}\\x = 7\end{array} \right.\end{array}\)

Vậy tập nghiệm của phương trình \(S = \left\{ { - \dfrac{1}{3};7} \right\}\)

c) \(\dfrac{{x - 3}}{5} - \dfrac{{7x + 1}}{3} = \dfrac{{2x - 5}}{{15}}\)

\( \Leftrightarrow \dfrac{{3\left( {x - 3} \right)}}{{15}} - \dfrac{{5\left( {7x + 1} \right)}}{{15}} = \dfrac{{2x - 5}}{{15}}\)

\(\begin{array}{l} \Leftrightarrow 3\left( {x - 3} \right) - 5\left( {7x + 1} \right) = 2x - 5\\ \Leftrightarrow 3x - 9 - 35x - 5 = 2x - 5\end{array}\) 

\(\begin{array}{l} \Leftrightarrow  - 32x - 14 = 2x - 5\\ \Leftrightarrow  - 32x + 2x =  - 5 + 14\\ \Leftrightarrow  - 30x = 9\\ \Leftrightarrow x =  - \dfrac{9}{{30}}\\ \Leftrightarrow x =  - \dfrac{3}{{10}}\end{array}\)

Vậy phương trình có nghiệm \(x =  - \dfrac{3}{{10}}\).

LG bài 2

Phương pháp giải:

Chuyển vế đưa về giải bất phương trình bậc nhất một ẩn

Lời giải chi tiết:

Ta có: \(13x - 7 \le 24x + 15\)

\(\begin{array}{l} \Leftrightarrow 13x - 24x \le 7 + 15\\ \Leftrightarrow  - 11x \le 22\\ \Leftrightarrow x \ge \dfrac{{ - 22}}{{11}}\\ \Leftrightarrow x \ge  - 2\end{array}\) 

Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x|x \ge  - 2} \right\}\)

LG bài 3

Phương pháp giải:

Giải bài toán bằng cách lập phương trình:

B1: Chọn ẩn và đặt điều kiện cho ẩn

B2: Lập phương trình và giải phương trình

B3: So sánh điều kiện và kết luận

Lời giải chi tiết:

Một miếng đất hình chữ nhật có chiều dài hơn chiều rộng là \(15m\). Nếu tăng chiều rộng \(5m\) và giảm chiều dài \(3m\) thì diện tích miếng đất tăng \(80{m^2}\). Tính kích thước miếng đất hình chữ nhật lúc đầu.

Gọi chiều rộng hình chữ nhật là \(x\) (m) \(\left( {x > 0} \right)\)

Chiều dài hình chữ nhật là \(x + 15\) (m)

Diện tích miếng đất hình chữ nhật ban đầu là: \(x\left( {x + 15} \right)\) \(\left( {{m^2}} \right)\)

Tăng chiều rộng 5m ta được chiều rộng mới là \(x + 5\) (m)

Giảm chiều dài 3m ta được chiều dài mới là \(x + 15 - 3 = x + 12\) (m)

Diện tích miếng đất mới là \(\left( {x + 5} \right)\left( {x + 12} \right)\) \(\left( {{m^2}} \right)\)

Vì diện tích hình chữ nhật mới tăng \(80{m^2}\) so với ban đầu nên ta có phương trình:

\(\left( {x + 5} \right)\left( {x + 12} \right) - x\left( {x + 15} \right) = 80\)

\( \Leftrightarrow {x^2} + 5x + 12x + 60\) \( - {x^2} - 15x = 80\)

\(\begin{array}{l} \Leftrightarrow 2x = 80 - 60\\ \Leftrightarrow 2x = 20\end{array}\)

\( \Leftrightarrow x = 10\) (thỏa mãn điều kiện) 

Vậy chiều rộng hình chữ nhật ban đầu là 10m

Chiều dài hình chữ nhật ban đầu là \(10 + 15 = 25m\)

LG bài 4

Phương pháp giải:

- Bước 1: Gọi ẩn và đặt điều kiện cho ẩn.

- Bước 2: Biểu diễn các đại lượng chưa biết và đã biết theo ẩn.

- Bước 3: Lập phương trình.

- Bước 4: Giải phương trình và kết luận nghiệm.

Lời giải chi tiết:

Gọi số tiền một cái bàn ủi ban đầu là \(x\) (đồng, \(0 < x < 350\,\,000\))

\( \Rightarrow \)Số tiền một bộ lau nhà ban đầu là \(350\,\,000 - x\) (đồng)

Giá tiền bàn ủi sau khi giảm \(10\% \) là: \(x - 10\% x = x - 0,1x\) \( = \left( {1 - 0,1} \right)x = 0,9x\)

Giá tiền bộ lau nhà sau khi giảm \(20\% \) là:

\(\begin{array}{l}\left( {350\,\,000 - x} \right) - 20\% .\left( {350\,\,000 - x} \right)\\ = \left( {350\,\,000 - x} \right) - 0,2\left( {350\,\,000 - x} \right)\\ = \left( {350\,\,000 - x} \right)\left( {1 - 0,2} \right)\\ = \left( {350\,\,000 - x} \right).0,8\\ = 280\,\,000 - 0,8x\end{array}\)

Sau khi giảm giá, An chỉ phải trả \(300\,\,000\) nên ta có phương trình: 

\(\begin{array}{l}0,9x + \left( {280\,\,000 - 0,8x} \right) = 300\,\,000\\ \Leftrightarrow 0,9x + 280\,\,000 - 0,8x = 300\,\,000\\ \Leftrightarrow 0,1x = 20\,000\\ \Leftrightarrow x = 200\,\,000\,\,\,\left( {TM} \right)\\ \Rightarrow y = 350\,\,000 - 200\,\,000 = 150\,\,000\end{array}\)

Vậy giá một cái bàn ủi ban đầu là \(200\,\,000\) đồng; giá một bộ lau nhà ban đầu là \(150\,\,000\) đồng.

LG bài 5

Phương pháp giải:

a) Chứng minh hai tam giác đồng dạng theo trường hợp góc - góc.

b) Từ câu a suy ra các tỉ số bằng nhau, từ đó suy ra đpcm.

c) Gọi D là giao điểm của IN và MC.

Chứng minh \(\Delta DMI \backsim \Delta DNC\) suy ra \(\Delta DNM \backsim \Delta DCI\)

Từ đó suy ra \(\widehat {DNM} = \widehat {DCI}\) và \(\widehat {HNM} = \widehat {MIC}\).

Chứng minh \(\Delta HNM \backsim \Delta HIC\) và suy ra đpcm.

Lời giải chi tiết:

Cho tam giác \(ABC\) vuông tại \(A\) \(\left( {AB < AC} \right)\). Kẻ đường cao \(AH\left( {H \in BC} \right)\).

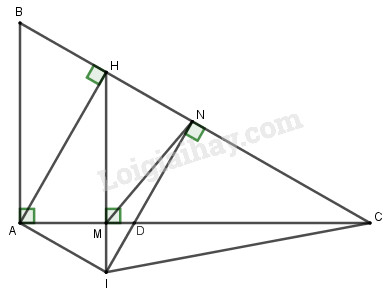
a) Chứng minh \(\Delta BHA\) đồng dạng với \(\Delta BAC\).

Tam giác ABC vuông tại A nên \(\widehat {BAC} = {90^0}\).

AH là đường cao của tam giác nên \(AH \bot BC \Rightarrow \widehat {AHB} = {90^0}\).

Xét \(\Delta BHA\) và \(\Delta BAC\) có:

\(\begin{array}{l}\widehat {BHA} = \widehat {BAC} = {90^0}\\\widehat B\,\,chung\end{array}\)

\( \Rightarrow \Delta BHA \backsim \Delta BAC\left( {g - g} \right)\) (đpcm)

b) Chứng minh \(A{H^2} = HB.HC\).

Theo câu a, \(\Delta BHA \backsim \Delta BAC\) \( \Rightarrow \widehat {BAH} = \widehat {BCA} = \widehat {HCA}\) (góc tương ứng)

Xét \(\Delta BHA\) và \(\Delta AHC\) có:

\(\begin{array}{l}\widehat {BHA} = \widehat {AHC} = {90^0}\\\widehat {BAH} = \widehat {HCA}\left( {cmt} \right)\\ \Rightarrow \Delta BHA \backsim \Delta AHC\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{BH}}{{AH}} = \dfrac{{HA}}{{HC}}\) (cạnh tương ứng)

\( \Rightarrow A{H^2} = HB.HC\) (đpcm).

c) Vẽ \(HM\) vuông góc với \(AC\) tại \(M\). Qua \(A\) vẽ đường thẳng song song với \(BC\) cắt đường thẳng \(HM\) tại \(I\), vẽ \(IN\) vuông góc với \(BC\) tại \(N\). Chứng minh rằng \(HM.IC = HC.MN\).

Gọi \(D\) là giao điểm của \(IN\) và \(MC\).

Xét \(\Delta DMI\) và \(\Delta DNC\) có:

\(\widehat {DMI} = \widehat {DNC} = {90^0}\)

\(\widehat {MDI} = \widehat {NDC}\) (đối đỉnh)

\( \Rightarrow \Delta DMI \backsim \Delta DNC\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{DM}}{{DN}} = \dfrac{{DI}}{{DC}}\) (cạnh tương ứng)

\( \Rightarrow \dfrac{{DM}}{{DI}} = \dfrac{{DN}}{{DC}}\)

Xét \(\Delta DMN\) và \(\Delta DIC\) có:

\(\widehat {MDN} = \widehat {IDC}\) (đối đỉnh)

\(\dfrac{{DM}}{{DI}} = \dfrac{{DN}}{{DC}}\left( {cmt} \right)\)

\( \Rightarrow \Delta DMN \backsim \Delta DIC\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {DNM} = \widehat {DCI}\) (góc tương ứng)

Lại có,

\(\begin{array}{l}\widehat {DNM} + \widehat {MNH} = {90^0}\\\widehat {DCI} + \widehat {CIM} = {90^0}\\ \Rightarrow \widehat {MNH} = \widehat {CIM} = \widehat {HIC}\end{array}\)

Xét \(\Delta HNM\) và \(\Delta HIC\) có:

\(\begin{array}{l}\widehat {MNH} = \widehat {HIC}\left( {cmt} \right)\\\widehat H\,\,chung\\ \Rightarrow \Delta HNM \backsim \Delta HIC\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{HM}}{{HC}} = \dfrac{{MN}}{{IC}}\) (cạnh tương ứng)

\( \Rightarrow HM.IC = HC.MN\)  (đpcm).

HẾT