Đề số 3 – Đề kiểm tra học kì 2 – Toán 9

Đề bài

Bài 1 (2,0 điểm):

Cho biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x  - 2}} + \dfrac{5}{{\sqrt x  + 2}} - \dfrac{{11\sqrt x  - 14}}{{x - 4}}\) với \(x \ge 0;x \ne 4\)

1. Rút gọn \(A.\)

2. Tìm các giá trị của \(x\)  để \(A <  - \dfrac{2}{3}.\)

Bài 2 (2,0 điểm):

1. Giải hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{{3x + y - 5}}{{x - y}} = 2\\x - 3y =  - 1\end{array} \right..\)

2. Trong vườn trường người ta xây một bồn hoa gồm hai hình tròn tâm \(A\)  và tâm \(B\) tiếp xúc ngoài với nhau, có \(AB = 3m\). Tính bán kính của mỗi hình tròn biết diện tích bồn hoa bằng \(4,68\pi {m^2}\) và bán kính hình tròn tâm \(A\) lớn hơn bán kính đường tròn tâm \(B.\)

Bài 3 (2,5 điểm):

Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right)\,:y = \left( {2m + 1} \right)x + 1 - {m^2}\,\) (với \(m\) là tham số).

1. Tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 1.\)

2. Tìm \(m\)  để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm nằm về hai phía của trục tung.

3. Tìm \(m\)  để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm phân biệt có tung độ là \({y_1};\,\,\,{y_2}\) thỏa mãn \({y_1} + {y_2} = 9.\)

Bài 4 (3 điểm):

Cho đường tròn \(\left( {O;R} \right)\) và dây cung \(BC\) cố định, \(A\) là điểm di động trên cung \(BC\) sao cho tam giác \(ABC\)nhọn. Hai đường phân giác trong của góc \(A\) và \(B\) cắt nhau ở \(I\)và thứ tự cắt đường tròn ở \(D,E\). Đường thẳng \(DE\) cắt \(BC,AC\) ở \(M,N\).

1. Chứng minh tứ giác \(AENI\) nội tiếp. Hãy chỉ ra một tứ giác nội tiếp tương tự.

2. Chứng minh tứ giác \(CMIN\) là hình thoi.

3. Chứng minh tam giác \(BDI\) cân. Tìm vị trí của \(A\) để \(AI\) có độ dài lớn nhất.

Bài 5 (0,5 điểm): 

Cho \(a,b,c\) là các số thực dương thỏa mãn: \(ab + bc + ac = 3abc.\) Tìm giá trị nhỏ nhất của biểu thức:

\(K = \dfrac{{{a^2}}}{{c\left( {{c^2} + {a^2}} \right)}} + \dfrac{{{b^2}}}{{a\left( {{a^2} + {b^2}} \right)}} \)\(\,+ \dfrac{{{c^2}}}{{b\left( {{b^2} + {c^2}} \right)}}\,.\)

LG bài 1

Phương pháp giải:

1. Quy đồng mẫu số rồi rút gọn biểu thức. 

2. Giải bất phương trình \(A <  - \dfrac{2}{3}\) để tìm \(x,\) đối chiếu với điều kiện rồi kết luận.

Lời giải chi tiết:

Cho biểu thức \(A = \dfrac{{\sqrt x }}{{\sqrt x  - 2}} + \dfrac{5}{{\sqrt x  + 2}} - \dfrac{{11\sqrt x  - 14}}{{x - 4}}\) với \(x \ge 0;x \ne 4\)

1. Rút gọn \(A.\)

Điều kiện xác định: \(x \ge 0;x \ne 4\)

\(\begin{array}{l}A = \dfrac{{\sqrt x }}{{\sqrt x  - 2}} + \dfrac{5}{{\sqrt x  + 2}} - \dfrac{{11\sqrt x  - 14}}{{x - 4}}\\\, = \dfrac{{\sqrt x }}{{\sqrt x  - 2}} + \dfrac{5}{{\sqrt x  + 2}} - \dfrac{{11\sqrt x  - 14}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right) + 5\left( {\sqrt x  - 2} \right) - \left( {11\sqrt x  - 14} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{x + 2\sqrt x  + 5\sqrt x  - 10 - 11\sqrt x  + 14}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{x - 4\sqrt x  + 4}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\,\\ = \dfrac{{{{\left( {\sqrt x  - 2} \right)}^2}}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}}.\end{array}\) 

Vậy \(A = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}}\)với \(x \ge 0;x \ne 4\).

2. Tìm các giá trị của \(x\)  để \(A <  - \dfrac{2}{3}.\)

Điều kiện xác định: \(x \ge 0;x \ne 4\)

\(\begin{array}{l}A <  - \dfrac{2}{3} \Leftrightarrow \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}} <  - \dfrac{2}{3}\\ \Leftrightarrow \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 2}} + \dfrac{2}{3} < 0\\ \Leftrightarrow \dfrac{{3\left( {\sqrt x  - 2} \right) + 2\left( {\sqrt x  + 2} \right)}}{{3\left( {\sqrt x  + 2} \right)}} < 0\\ \Leftrightarrow \dfrac{{5\sqrt x  - 2}}{{3\left( {\sqrt x  + 2} \right)}} < 0\end{array}\)

\( \Leftrightarrow 5\sqrt x  - 2 < 0\,\,\)(\(do:3\left( {\sqrt x  + 2} \right) > 0\) với mọi \(x \ge 0;x \ne 4\))

\( \Leftrightarrow \sqrt x  < \dfrac{2}{5} \Leftrightarrow x < \dfrac{4}{{25}}\)

Kết hợp với ĐKXĐ ta có: \(0 \le x < \dfrac{4}{{25}}\) thì \(A <  - \dfrac{2}{3}\)

LG bài 2

Phương pháp giải:

1. Đặt điều kiện, biến đổi hệ phương trình say đó giải hệ phương trình bằng phương pháp cộng đại số.

2. Gọi bán kính hình tròn tâm \(A\)  và tâm \(B\)  lần lượt là \(x;\,\,y\,\,\,\left( m \right),\,\,\,\left( {0 < y < x < 3} \right).\) 

Biểu diễn các dữ kiện đã biết theo hai ẩn đã gọi.

Lập hệ phương trình, giải hệ phương trình.

So sánh với điều kiện rồi kết luận.

Lời giải chi tiết:

1. Giải hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{{3x + y - 5}}{{x - y}} = 2\\x - 3y =  - 1\end{array} \right..\)

Điều kiện xác định:  \(x \ne y\)

\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{{3x + y - 5}}{{x - y}} = 2\\x - 3y =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x + y - 5 = 2\left( {x - y} \right)\\x - 3y =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x + y - 5 = 2x - 2y\\x - 3y =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 3y = 5\\x - 3y =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 3y + x - 3y = 5 + \left( { - 1} \right)\\x - 3y =  - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2x = 4\\3y = x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2\\3y = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\,\,\,\,\left( {tm} \right)\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {2;1} \right).\)

2. Trong vườn trường người ta xây một bồn hoa gồm hai hình tròn tâm \(A\)  và tâm \(B\) tiếp xúc ngoài với nhau, có \(AB = 3m\). Tính bán kính của mỗi hình tròn biết diện tích bồn hoa bằng \(4,68\pi {m^2}\) và bán kính hình tròn tâm \(A\) lớn hơn bán kính đường tròn tâm \(B.\)

Gọi bán kính hình tròn tâm \(A\)  và tâm \(B\)  lần lượt là \(x;\,\,y\,\,\,\left( m \right),\,\,\,\left( {0 < y < x < 3} \right).\)

Vì 2 đường tròn tiếp xúc ngoài với nhau nên: \(x + y = AB = 3\,\,\,\,\left( m \right)\,\,\,\,\,\left( 1 \right)\)

Diện tích của hai vườn hoa hình tròn tâm \(A\) và tâm \(B\) lần lượt là: \(\pi {x^2}\,\,\left( {{m^2}} \right)\) và \(\pi {y^2}\,\,\left( {{m^2}} \right).\)

Lại có diện tích bồn hoa bằng tổng diện tích của hai hình tròn bằng \(4,68\pi \left( {{m^2}} \right)\) nên:

\(\pi .{x^2} + \pi .{y^2} = 4,68\pi \left( {{m^2}} \right) \Rightarrow {x^2} + {y^2} = 4,68\,\,\,\left( 2 \right)\)

Từ (1) và (2) ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 3\\{x^2} + {y^2} = 4,68\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3 - y\\{\left( {3 - y} \right)^2} + {y^2} = 4,68\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3 - y\\2{y^2} - 6y + 4,32 = 0\,\,\,\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3 - y\\\left( {9y - 5} \right)\left( {6y - 5} \right) = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3 - y\\\left[ \begin{array}{l}y = 1,8\,\,\\y = 1,2\,\,\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 1,8\\y = 1,2\end{array} \right.\,\,\,\left( {tm\,\,do\,\,\,x > y} \right)\\\left\{ \begin{array}{l}x = 1,2\\y = 1,8\,\end{array} \right.\,\,\,\left( {ktm\,\,\,do\,\,\,x > y} \right)\end{array} \right..\end{array}\)

Vậy bán kính của hai khu vường hình tròn tâm \(A\) và tâm \(B\) lần lượt là: \(1,8m\) và \(1,2m.\)

LG bài 3

Phương pháp giải:

1. Thay \(m = 1\) để tìm phương trình đường thẳng \(\left( d \right)\), giải phương trình hoành độ giao điểm để tìm giao điểm của \(\left( P \right)\) và \(\left( d \right)\) để tìm hoành độ các giao điểm.

Thay hoành độ giao điểm vừa tìm được vào công thức hàm số của \(\left( d \right)\) hoặc \(\left( P \right)\) để tìm tung độ các giao điểm.

2. Hai điểm nằm về hai phía trục tung khi có các giao điểm có hoành độ trái dấu.

Khi đó phương trình hoành độ giao điểm có hai nghiệm trái dấu \( \Leftrightarrow ac < 0.\)

3. Xét phương trình hoành độ giao điểm \(\left( * \right)\)  của \(\left( d \right)\) và \(\left( P \right).\)

\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta  > 0.\)

Biểu diễn \(y_1;y_2\) theo \(x_1;x_2\) rồi sử dụng hệ thức Vi-et để có phương trình ẩn \(m\). Giải phương trình ta tìm được \(m\)

Lời giải chi tiết:

Cho parabol \(\left( P \right):\,\,\,y = {x^2}\) và đường thẳng \(\left( d \right)\,:y = \left( {2m + 1} \right)x + 1 - {m^2}\,\) (với \(m\) là tham số).

1. Tìm tọa độ các giao điểm của \(\left( P \right)\) và \(\left( d \right)\) khi \(m = 1.\)

Khi \(m = 1\) ta có: \(\left( d \right):\,\,\,y = 3x.\)

Xét phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( d \right)\) ta có:

\({x^2} = 3x \Leftrightarrow {x^2} - 3x = 0 \Leftrightarrow x\left( {x - 3} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y = 0 \Rightarrow O\left( {0;\,\,0} \right)\\x = 3 \Rightarrow y = 3.3 = 9 \Rightarrow A\left( {3;\,\,9} \right)\end{array} \right.\)

Vậy khi \(m = 1\) thì giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là hai điểm \(\left( {0;0} \right);\left( {3;9} \right)\).

2. Tìm \(m\)  để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm nằm về hai phía của trục tung.

Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) ta có:

\(\begin{array}{l}{x^2} = \left( {2m + 1} \right)x + 1 - {m^2}\\ \Leftrightarrow {x^2} - \left( {2m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\left( * \right)\end{array}\)

\(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt nằm về hai phía của trục tung \( \Leftrightarrow \left( * \right)\) có hai nghiệm trái dấu

\( \Leftrightarrow ac < 0 \Leftrightarrow {m^2} - 1 < 0\) \( \Leftrightarrow \left( {m - 1} \right)\left( {m + 1} \right) < 0 \Leftrightarrow  - 1 < m < 1.\)

Vậy \( - 1 < m < 1\) thỏa mãn bài toán.

3. Tìm \(m\)  để \(\left( P \right)\) cắt \(\left( d \right)\) tại hai điểm phân biệt có tung độ là \({y_1};\,\,\,{y_2}\) thỏa mãn \({y_1} + {y_2} = 9.\)

Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\) ta có:

\(\begin{array}{l}{x^2} = \left( {2m + 1} \right)x + 1 - {m^2}\\ \Leftrightarrow {x^2} - \left( {2m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\left( * \right)\end{array}\)

Đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \( \Leftrightarrow \left( * \right)\) có hai nghiệm phân biệt

\(\begin{array}{l} \Leftrightarrow \Delta  > 0 \Leftrightarrow {\left( {2m + 1} \right)^2} - 4\left( {{m^2} - 1} \right) > 0\\ \Leftrightarrow 4{m^2} + 4m + 1 - 4{m^2} + 4 > 0\\ \Leftrightarrow 4m + 5 > 0\\ \Leftrightarrow m >  - \dfrac{5}{4}.\end{array}\)

Vậy với \(m >  - \dfrac{5}{4}\) thì đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt \(A\left( {{x_1};\,\,x_1^2} \right),\,\,\,B\left( {{x_2};\,\,x_2^2} \right).\)

Áp dụng định lý Vi-ét ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m + 1\\{x_1}{x_2} = {m^2} - 1\end{array} \right..\)  

Theo đề bài ta có: \({y_1} + {y_2} = 9\)

\(\begin{array}{l} \Leftrightarrow x_1^2 + x_2^2 = 9\\ \Leftrightarrow x_1^2 + 2{x_1}{x_2} + x_2^2 - 2{x_1}{x_2} = 9\\ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - 9 = 0\\ \Leftrightarrow {\left( {2m + 1} \right)^2} - 2\left( {{m^2} - 1} \right) - 9 = 0\\ \Leftrightarrow 4{m^2} + 4m + 1 - 2{m^2} + 2 - 9 = 0\\ \Leftrightarrow 2{m^2} + 4m - 6 = 0\\ \Leftrightarrow {m^2} + 2m - 3 = 0\\ \Leftrightarrow {m^2} + 3m - m - 3 = 0\\ \Leftrightarrow m\left( {m + 3} \right) - \left( {m + 3} \right) = 0\\ \Leftrightarrow \left( {m + 3} \right)\left( {m - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m + 3 = 0\\m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m =  - 3\,\,\,\,\left( {ktm} \right)\\m = 1\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy \(m = 1\) thỏa mãn bài toán.

LG bài 4

Phương pháp giải:

1. Sử dụng các dấu hiệu nhận biết của tứ giác nội tiếp.

2. Sử dụng các dấu hiệu nhận biết hình thoi.

Lời giải chi tiết:

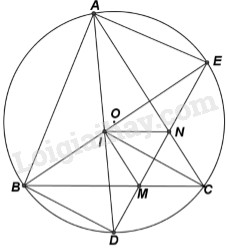
1. Chứng minh tứ giác \(AENI\) nội tiếp. Hãy chỉ ra một tứ giác nội tiếp tương tự.

Ta có \(AD;BE\) là phân giác của góc \(A\) và \(B\) nên:

 \(\left\{ \begin{array}{l}\angle BAD = \angle CAD\\\angle ABE = \angle CBE\end{array} \right.\)

\( \Rightarrow \left\{ \begin{array}{l}cung\,BD = cung\,CD\\cung\,AE = cung\,EC\end{array} \right.\) (tính chất góc nội tiếp bằng nhau thì chắn các cung bằng nhau).

Lại có: \(\angle DAC\) là góc nội tiếp chắn cung \(CD\) 

Và \(\angle BED\) là góc nội tiếp chắn cung \(BD\)

\( \Rightarrow \angle DAC = \angle BED\) (hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau).

Hay \(\angle IAN = \angle IEN.\)

Xét tứ giác \(IAEN\) ta có:

\(\angle IAN = \angle IEN\,\,\,\,\left( {cmt} \right)\)

Mà hai góc này là hai góc có đỉnh cùng kề cạnh \(AE\)

\( \Rightarrow IAEN\) là tứ giác nội tiếp (dhnb).

Chứng minh tương tự ta có tứ \(BDMI\) cũng là tứ giác nội tiếp.

2. Chứng minh tứ giác \(CMIN\) là hình thoi.

Do tứ giác \(AENI\) nội tiếp (cmt)  \( \Rightarrow \angle AEI = \angle ANI\) (hai góc nội tiếp cùng chắn cung \(AI\))

Lại có: \(\angle AEI = \angle ACB\) (hai góc nội tiếp cùng chắn cung \(AB\) của đường tròn \(\left( O \right)\))

\( \Rightarrow \angle ANI = \angle ACB\,\,\,\left( { = \angle AEI} \right)\)

Mà hai góc này là hai góc đồng vị

\( \Rightarrow NI//BC\,\,\,\,hay\,\,\,NI//CM\)

Tương tự ta chứng minh được \(\angle BMI = \angle ACB\,\,\,\,\left( {\angle BDI} \right)\)

\( \Rightarrow IM//AC\,\,\,\,\,hay\,\,\,\,\,IM//CN\)

Xét tứ giác \(IMCN\) có: \(\left\{ \begin{array}{l}NI//CM\\IM//CN\end{array} \right.\,\,\,\,\left( {cmt} \right)\)

\( \Rightarrow IMCN\) là hình bình hành  (dhnb).

Lại có hai đường phân giác trong của góc \(A\) và \(B\) cắt nhau ở \(I\) (gt)

\( \Rightarrow CI\) là đường phân giác của \(\angle BCA\) của \(\Delta ABC.\)

\( \Rightarrow CI\) là phân giác của góc \(\angle MCN\)

\( \Rightarrow \) Hình bình hành \(INCM\) có đường chéo \(CI\) là đường phân giác của \(\angle MCI\)

\( \Rightarrow IMCN\) là hình thoi. (đpcm)

3. Chứng minh tam giác \(BDI\) cân. Tìm vị trí của \(A\) để \(AI\) có độ dài lớn nhất.

Ta có tứ giác \(BIMD\) là tứ giác nội tiếp (cmt)

\( \Rightarrow \angle BID = \angle BMD\) (hai góc nội tiếp cùng chắn cung \(BD\))

Xét đường tròn \(\left( O \right)\) ta có:

\(\angle BMD\) là góc có đỉnh nằm trong đường tròn chắn cung \(BD\) và cung \(EC\)

\( \Rightarrow \angle BMD = \dfrac{1}{2}\left( {cung\,\,BD + cung\,EC} \right)\) \( = \dfrac{1}{2}\left( {cung\,\,CD + cung\,\,EC} \right) = \dfrac{1}{2}cung\,\,DE\)

Mà \(\angle EBD\) là góc nội tiếp chắn cung \(DE\)

\(\begin{array}{l} \Rightarrow \angle EBD = \angle IBD = \dfrac{1}{2}\,\,cung\,\,DE\\ \Rightarrow \angle IBD = \angle BMD\,\,\,\left( { = \dfrac{1}{2}\,\,cung\,\,DE} \right)\\ \Rightarrow \angle IBD = \angle BID\,\,\,\left( { = \angle BMD} \right)\end{array}\)

\( \Rightarrow \Delta BID\) cân tại \(D.\) (đpcm).

LG bài 5

Phương pháp giải:

Áp dụng bất đẳng thức Cô-si cho 2 số \(a,b\) không âm: \(a + b \ge 2\sqrt {ab} \)

Dấu “=” xảy ra khi \(a = b.\)

Lời giải chi tiết:

Có \(\dfrac{{{a^2}}}{{c({c^2} + {a^2})}} = \dfrac{{{a^2} + {c^2} - {c^2}}}{{c({c^2} + {a^2})}}\)\(\, = \dfrac{1}{c} - \dfrac{c}{{{c^2} + {a^2}}}\mathop  \ge \limits^{Cô-si} \dfrac{1}{c} - \dfrac{c}{{2\sqrt {{c^2}.\,\,{a^2}} }} \)\(\,= \dfrac{1}{c} - \dfrac{1}{{2a}}\)

\( \Rightarrow \dfrac{{{a^2}}}{{c({c^2} + {a^2})}} \ge \dfrac{1}{c} - \dfrac{1}{{2a}}\)

Và tương tự ta có:

\(\dfrac{{{b^2}}}{{a({a^2} + {b^2})}} \ge \dfrac{1}{a} - \dfrac{1}{{2b}}\)

\(\dfrac{{{c^2}}}{{c({c^2} + {b^2})}} \ge \dfrac{1}{b} - \dfrac{1}{{2c}}\)

\( \Rightarrow P \ge \left( {\dfrac{1}{c} - \dfrac{1}{{2a}}} \right) + \left( {\dfrac{1}{a} - \dfrac{1}{{2b}}} \right) \)\(\,+ \left( {\dfrac{1}{b} - \dfrac{1}{{2c}}} \right) = \dfrac{1}{2}\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \)\(\,= \dfrac{{ab + bc + ca}}{{2abc}} = \dfrac{3}{2}\)

\( \Rightarrow \) GTNN của \(P\) là \(\dfrac{3}{2}\) \( \Leftrightarrow a = b = c = 1\).

Nguồn sưu tầm