Đề số 3 – Đề kiểm tra học kì 2 – Toán 8
Đáp án và lời giải chi tiết Đề số 3 - Đề kiểm tra học kì 2 (Đề thi học kì 2) - Toán 8
Đề bài
Câu 1 (3,25 điểm): Giải các phương trình sau:
\(\begin{array}{l}a)\,\,2\left( {4x - 7} \right) = 3\left( {x + 1} \right) + 18\\b)\,\,\dfrac{{3x + 2}}{2} + \dfrac{{5 - 2x}}{3} = \dfrac{{11}}{6}\end{array}\)
\(\begin{array}{l}c)\,\,\left| {x - 1} \right| + 7 = 3x\\d)\,\,\dfrac{{x + 2}}{{x + 3}} + \dfrac{{2x - 1}}{{x - 3}} = \dfrac{{13x - 9}}{{{x^2} - 9}}\end{array}\)
Câu 2 (1,25 điểm): Giải bất phương trình và biểu diễn tập nghiệm trên trục số: \(\dfrac{{3x + 5}}{4} - \dfrac{{x - 4}}{6} \le \dfrac{{3x + 7}}{3}.\)
Câu 3 (1,5 điểm):
Một ô tô đi từ A đến B trong một thời gian dự định. Nếu xe chạy với vận tốc 40 km/h thì đến B chậm hơn 30 phút so với thời gian dự định. Nếu xe chạy với vận tốc 50 km/h thì đến B sớm hơn 24 phút so với thời gian dự đinh. Tính chiều dài quãng đường AB.
Câu 4 (1 điểm):
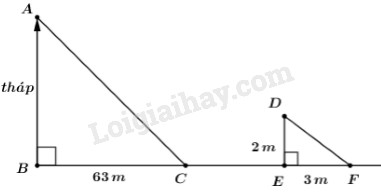
Bóng của một tháp trên mặt đất có độ dài 63m. Cùng thời điểm đó, một cây cột cao 2m cắm vuông góc với mặt đất có bóng dài 3m. Tính chiều cao của tháp.
Câu 5 (3 điểm):
Cho tam giác nhọn \(ABC\) có ba đường cao \(AD,\,\,BE\) và \(CF\) cắt nhau tại \(H.\)
a) Chứng minh: \(\Delta ABE \backsim \Delta ACF,\) từ đó suy ra \(AB.AF = AC.AE.\)
b) Chứng minh: \(DB.DC = DA.DH.\)
c) Gọi \(I\) là trung điểm của \(BC.\) Đường thẳng vuông góc với \(IH\) tại \(H\) cắt \(AB\) và \(AC\) lần lượt tại \(M\) và \(N.\) Chứng minh \(\Delta AHN \backsim \Delta BIH\) và \(H\) là trung điểm của \(MN.\)
LG câu 1
Phương pháp giải:
a) Sử dụng quy tắc chuyển vế đổi dấu để giải phương trình.
b) Quy đồng mẫu, khử mẫu, đưa phương trình về dạng \(ax + b = 0\) rồi giải phương trình.
c) Giải phương trình chứa dấu giá trị tuyệt đối: \(\left| {f\left( x \right)} \right| = g\left( x \right)\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\f\left( x \right) = g\left( x \right)\end{array} \right.\\\left\{ \begin{array}{l}f\left( x \right) < 0\\ - f\left( x \right) = g\left( x \right)\end{array} \right.\end{array} \right.\)
d) Giải phương trình chứa ẩn ở mẫu:
+) Đặt điều kiện.
+) Quy đồng khử mẫu rồi đưa phương trình về dạng \(ax + b = 0\) rồi giải phương trình.
+) Đối chiếu với điều kiện xác định rồi kết luận.
Lời giải chi tiết:
\(\begin{array}{l}a)\,\,\,2\left( {4x - 7} \right) = 3\left( {x + 1} \right) + 18\\ \Leftrightarrow 8x - 14 = 3x + 3 + 18\\ \Leftrightarrow 5x = 35\\ \Leftrightarrow x = 7.\end{array}\)
Vậy phương trình có nghiệm duy nhất \(x = 7.\)
\(\begin{array}{l}b)\,\,\,\dfrac{{3x + 2}}{2} + \dfrac{{5 - 2x}}{3} = \dfrac{{11}}{6}\\ \Leftrightarrow 3\left( {3x + 2} \right) + 2\left( {5 - 2x} \right) = 11\\ \Leftrightarrow 9x + 6 + 10 - 4x = 11\\ \Leftrightarrow 5x = 11 - 6 - 10\\ \Leftrightarrow 5x = - 5\\ \Leftrightarrow x = - 1.\end{array}\)
Vậy phương trình có nghiệm duy nhất \(x = - 1.\)
\(\begin{array}{l}c)\,\,\left| {x - 1} \right| + 7 = 3x\\ \Leftrightarrow \left| {x - 1} \right| = 3x - 7\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 \ge 0\\x - 1 = 3x - 7\end{array} \right.\\\left\{ \begin{array}{l}x - 1 < 0\\ - \left( {x - 1} \right) = 3x - 7\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x - 1 = 3x - 7\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\ - x + 1 = 3x - 7\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\3x - x = - 1 + 7\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x + 3x = 7 + 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\2x = 6\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\4x = 8\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x = 3\end{array} \right.\\\left\{ \begin{array}{l}x < 1\\x = 2\end{array} \right.\end{array} \right.\\ \Leftrightarrow x = 3.\end{array}\)
Vậy phương trình có nghiệm duy nhất \(x = 3.\)
\(d)\,\,\dfrac{{x + 2}}{{x + 3}} + \dfrac{{2x - 1}}{{x - 3}} = \dfrac{{13x - 9}}{{{x^2} - 9}}\) Điều kiện: \(x \ne 3;\,\,x \ne - 3.\)
\( \Leftrightarrow \,\,\dfrac{{x + 2}}{{x + 3}} + \dfrac{{2x - 1}}{{x - 3}} = \dfrac{{13x - 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
\( \Leftrightarrow \dfrac{{\left( {x + 2} \right)\left( {x - 3} \right) + \left( {2x - 1} \right)\left( {x + 3} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)\( = \dfrac{{13x - 9}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}\)
\( \Leftrightarrow \left( {x + 2} \right)\left( {x - 3} \right) + \left( {2x - 1} \right)\left( {x + 3} \right)\)\( = 13x - 9\)
\(\begin{array}{l} \Leftrightarrow {x^2} - x - 6 + 2{x^2} + 5x - 3 = 13x - 9\\ \Leftrightarrow 3{x^2} - 9x = 0\\ \Leftrightarrow 3x\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}3x = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\,\left( {tm} \right)\\x = 3\,\,\left( {ktm} \right)\end{array} \right.\end{array}\)
Vậy phương trình có nghiệm là \(x = 0.\)
LG câu 2
Phương pháp giải:
+) Quy đồng, khử mẫu của bất phương trình.
+) Giải bất phương trình bằng các quy tắc cơ bản.
+) Kết luận nghiệm của bất phương trình và biểu diễn tập nghiệm trên trục số.
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,\,\dfrac{{3x + 5}}{4} - \dfrac{{x - 4}}{6} \le \dfrac{{3x + 7}}{3}\\ \Leftrightarrow 3\left( {3x + 5} \right) - 2\left( {x - 4} \right) \le 4\left( {3x + 7} \right)\\ \Leftrightarrow 9x + 15 - 2x + 8 \le 12x + 28\\ \Leftrightarrow 12x - 9x + 2x \ge -28 + 15 + 8\\ \Leftrightarrow 5x \ge -5\\ \Leftrightarrow x \ge -1.\end{array}\)
Vậy bất phương trình có tập nghiệm \(S = \left\{ {x\,\,|\,\,x \ge -1} \right\}.\)
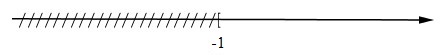
LG câu 3
Phương pháp giải:
Gọi chiều dài quãng đường AB là \(x\,\,\left( {km} \right),\,\,\left( {x > 0} \right).\)
Biểu diễn thời gian ô tô đi với vận tốc 40 km/h và khi đi với vận tốc 50 km/h.
Theo đề bài, biểu diễn mối quan hệ thời gian ô tô đi hết quãng đường với vận tốc khác nhau để lập phương trình.
Giải phương trình vừa lập được, đối chiếu với điều kiện xác định rồi kết luận.
Lời giải chi tiết:
Đổi 30 phút = \(\frac{1}{2}\) giờ và 24 phút = \(\frac{2}{5}\)giờ
Gọi chiều dài quãng đường AB là \(x\,\,\left( {km} \right),\,\,\left( {x > 0} \right).\)
Thời gian ô tô đi hết quãng đường AB với vận tốc \(40\,\,km/h\) là: \(\dfrac{x}{{40}}\,\,\,\left( h \right).\)
Thời gian ô tô đi hết quãng đường AB với vận tốc \(50\,\,km/h\) là: \(\dfrac{x}{{50}}\,\,\,\left( h \right).\)
Do nếu xe chạy với vận tốc 40 km/h thì đến B chậm hơn 30 phút so với thời gian dự định và nếu xe chạy với vận tốc 50 km/h thì đến B sớm hơn 24 phút so với thời gian dự đinh nên:
\(\begin{array}{l}\frac{x}{{40}} - \frac{1}{2} = \frac{x}{{50}} + \frac{2}{5}\\ \Leftrightarrow \frac{x}{{40}} - \frac{x}{{50}} = \frac{9}{{10}}\\ \Leftrightarrow \frac{x}{4} - \frac{x}{5} = 9\\ \Leftrightarrow 5x - 4x = 180\\ \Leftrightarrow x = 180.\end{array}\)
Vậy quãng đường AB dài \(180\,\,km.\)
LG câu 4
Phương pháp giải:
Sử dụng các định lý của tam giác đồng dạng để tính chiều cao của tháp.
Lời giải chi tiết:
Vì ở cùng 1 thời điểm nên \(\angle ACB = \angle DFE\)
\(\begin{array}{l} \Rightarrow \Delta ABC \backsim \Delta DEF\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AB}}{{DE}} = \dfrac{{BC}}{{EF}}\end{array}\)
\( \Leftrightarrow AB = \dfrac{{DE.BC}}{{EF}}\)\( = \dfrac{{2.63}}{3} = 42\,\left( m \right).\)
Vậy chiều cao của tháp là \(42\,m.\)
LG câu 5
Phương pháp giải:
a) Chứng minh hai tam giác đồng dạng theo TH góc – góc, từ đó suy ra các cặp cạnh tương ứng tỉ lệ.
b) Chứng minh \(\Delta DHB \backsim \Delta DAC\,\,\left( {g - g} \right)\) sau đó suy ra các cặp cạnh tương ứng tỉ lệ và suy ra đẳng thức cần chứng minh.
c) Chứng minh \(\Delta AHN \backsim \Delta BIH\,\,\left( {g - g} \right)\) và \(\Delta AHM \backsim \Delta CIH\,\,\,\left( {g - g} \right)\) để từ đó suy ra \(H\) là trung điểm của \(MN.\)
Lời giải chi tiết:
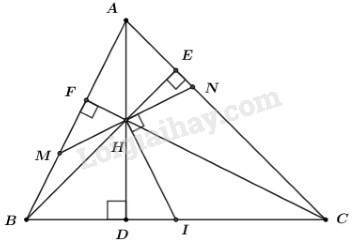
a) Chứng minh: \(\Delta ABE \backsim \Delta ACF,\) từ đó suy ra \(AB.AF = AC.AE.\)
Xét \(\Delta ABE\) và \(\Delta ACF\) ta có:
\(\begin{array}{l}\angle A\,\,\,\,chung\\\angle AEB = \angle AFC = {90^0}\\ \Rightarrow \Delta ABE \backsim \Delta ACF\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AB}}{{AC}} = \dfrac{{AE}}{{AF}}\\ \Leftrightarrow AB.AF = AC.AE\,\,\end{array}\)
b) Chứng minh: \(DB.DC = DA.DH.\)
Ta có: \(\angle DAC + \angle ACD = {90^0}\) (do \(\Delta ADC\) vuông tại D)
\(\angle EBC + \angle ACD = {90^0}\) (do \(\Delta BEC\) vuông tại E)
\( \Rightarrow \angle EBC = \angle DAC\) (cùng phụ với \(\angle ACD\))
Hay \(\angle DAC = \angle HBD.\)
Xét \(\Delta DAC\) và \(\Delta DBH\) ta có:
\(\begin{array}{l}\angle ADC = \angle HDB = {90^0}\\\angle HBD = \angle DAC\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta DAC \backsim \Delta DBH\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{DA}}{{DB}} = \dfrac{{DC}}{{DH}}\\ \Leftrightarrow DA.DH = DB.DC\end{array}\)
c) Gọi \(I\) là trung điểm của \(BC.\) Đường thẳng vuông góc với \(IH\) tại \(H\) cắt \(AB\) và \(AC\) lần lượt tại \(M\) và \(N.\) Chứng minh và \(H\) là trung điểm của \(MN.\)
Ta có: \(\angle EHN = \angle MHB\) (hai góc đối đỉnh)
Mà \(\angle ENH + \angle EHN = {90^0}\) (do \(\Delta EHN\) vuông tại \(E\))
\(\angle MHN + \angle BHI = {90^0}\,\) \(\,\left( {IH \bot MH} \right)\)
\( \Rightarrow \angle BHI = \angle ANH\) (tính chất bắc cầu).
Xét \(\Delta AHN\) và \(\Delta BIH\) ta có:
\(\begin{array}{l}\angle HAN = \angle HBI\,\,\,\left( {cmt} \right)\\\angle ANH = \angle BHI\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AHN \backsim \Delta BIH\,\,\left( {g - g} \right)\,\\ \Rightarrow \dfrac{{AH}}{{BI}} = \dfrac{{HN}}{{IH}} = \dfrac{{AN}}{{BH}}.\end{array}\)
Ta có: \(\angle FMH + \angle FHM = {90^0}\) (do \(\Delta FHM\) vuông tại \(F\))
\(\angle IHC + \angle CHN = {90^0}\,\,\,\left( {do\,\,\,IH \bot HN} \right)\)
Mà \(\angle FHM = \angle NHC\) (hai góc đối đỉnh)
\( \Rightarrow \angle IHC = \angle FMH.\)
Xét \(\Delta HMA\) và \(\Delta CIH\) ta có:
\(\angle MAH = \angle HCI\) (cùng phụ với \(\angle ABD\))
\(\begin{array}{l}\angle AMH = \angle IHC\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AHM \backsim \Delta CIH\,\,\,\left( {g - g} \right)\\ \Rightarrow \dfrac{{AH}}{{CI}} = \dfrac{{MA}}{{CH}} = \dfrac{{HM}}{{IH}}\end{array}\)
Lại có \(I\) là trung điểm của \(BC \Rightarrow BI = CI.\)
\( \Rightarrow \dfrac{{AH}}{{BI}} = \dfrac{{AH}}{{CI}}\) \( = \dfrac{{HN}}{{IH}} = \dfrac{{HM}}{{IH}}\)\( \Rightarrow HN = HM\)
Hay \(H\) là trung điểm của \(MN\,\) (đpcm)
Nguồn sưu tầm
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề số 3 – Đề kiểm tra học kì 2 – Toán 8 timdapan.com"







