Đề số 11 - Đề kiểm tra học kì 1 - Toán 7
Đáp án và lời giải chi tiết Đề số 11 - Đề kiểm tra học kì 1 (Đề thi học kì 1) - Toán 7
Đề bài
I. Phần trắc nghiệm (2 điểm): Hãy chọn đáp án đúng trong các câu sau:
Câu 1 :Công thức cho ta quan hệ tỉ lệ nghịch giữa \(x\) và \(y\) là:
A.\(xy = 1,25\) B.\(\dfrac{x}{y} = 4\)
C.\(x + y = 5\) D.\(x - y = 3\)
Câu 2 : Căn bậc hai của \(16\) là:
A.\(4\) B.\( - 4\)
C.\( \pm 4\) D.\(196\)
Câu 3 : Số nào dưới đây viết được dưới dạng số thập phân hữu hạn:
A.\(\dfrac{3}{{22}}\) B.\(\dfrac{{21}}{{12}}\)
C.\(\dfrac{7}{3}\) D.\(\dfrac{5}{{14}}\)
Câu 4 : Tam giác \(ABC\) có \(\angle A:\angle B:\angle C = 2:3:4\). Số đo góc A bằng:
A.\({20^0}\) B.\({40^0}\)
C.\({60^0}\) D.\({80^0}\)
II. Tự luận (8 điểm):
Câu 5 :Tính hợp lý nếu có thể
\(\begin{array}{l}a)\,\,\dfrac{2}{{13}} \cdot \left( {\dfrac{{ - 5}}{3}} \right) + \dfrac{{11}}{{13}} \cdot \left( {\dfrac{{ - 5}}{3}} \right)\\b)\,\,\,{\left( { - \dfrac{1}{3}} \right)^2} + \,{\left( { - \dfrac{1}{3}} \right)^3}.27 + \,{\left( { - \dfrac{{2017}}{{2018}}} \right)^0}\\c)\,\,\left( {1,2 - \sqrt {\dfrac{1}{4}} } \right):1\dfrac{1}{{20}} + \left| {\dfrac{3}{4} - 1,25} \right| - {\left( {\dfrac{{ - 3}}{2}} \right)^2}\end{array}\)
Câu 6 :Tìm \(x\) biết:
\(a)\,\,\dfrac{3}{5}.\left( {2x - \dfrac{1}{3}} \right) + \dfrac{4}{{15}} = \,\dfrac{{12}}{{30}}\\b)\,\,{( - 0,2)^x} = \dfrac{1}{{25}}\\c)\,\,\left| {x - 1} \right| - \dfrac{3}{{12}} = {\left( { - \dfrac{1}{2}} \right)^2}\)
Câu 7 :Ba lớp 7A, 7B, 7C đã đóng góp một số sách để hưởng ứng việc xây dựng mỗi lớp có một thư viện riêng. Biết số sách góp được của lớp 7A, 7B, 7C tỉ lệ với \(6,\,\,4,\,\,5\) và tổng số sách góp được của lớp 7A với lớp 7B hơn số sách của lớp 7C là \(40\) quyển. Tính số sách của mỗi lớp góp được.
Câu 8 :Cho \(\Delta ABC\) có \(AB = AC,\,\,\,M\) là trung điểm của \(BC\).
a) Chứng minh \(\Delta AMB = \Delta AMC\).
b) Từ \(M\) kẻ \(ME \bot AB\,\,(E \in AB)\,,\,\,MF \bot AC\,\,(F \in AC)\,\). Chứng minh \(AE = AF\).
c) Chứng minh: \(EF\) // \(BC\).
Câu 9 (1 điểm): Tìm \(x,y,z\) biết rằng: \(\dfrac{x}{{y + z + 1}} = \dfrac{y}{{x + z + 1}} = \dfrac{z}{{x + y - 2}} = x + y + z\)
Lời giải chi tiết
I. Trắc nghiệm
|
1. A |
2. C |
3. B |
4. B |
II. TỰ LUẬN: (7 điểm)
Câu 5:
\(\begin{array}{l}a)\,\,\dfrac{2}{{13}} \cdot \left( {\dfrac{{ - 5}}{3}} \right) + \dfrac{{11}}{{13}} \cdot \left( {\dfrac{{ - 5}}{3}} \right)\,\,\,\\\,\,\,\, = \left( {\dfrac{{ - 5}}{3}} \right) \cdot \left( {\dfrac{2}{{13}} + \dfrac{{11}}{{13}}} \right)\,\,\,\,\\\,\,\,\, = \left( {\dfrac{{ - 5}}{3}} \right) \cdot \dfrac{{13}}{{13}}\,\,\,\,\\\,\,\,\, = \left( {\dfrac{{ - 5}}{3}} \right).1\,\,\,\,\,\,\,\\\,\,\,\, = \dfrac{{ - 5}}{3}\,\,\,\,\,\,\,\,\,\,\,\end{array}\)\(\begin{array}{l}\,b)\,\,\,{\left( { - \dfrac{1}{3}} \right)^2} + \,{\left( { - \dfrac{1}{3}} \right)^3}.27 + \,{\left( { - \dfrac{{2017}}{{2018}}} \right)^0}\\ = \dfrac{1}{9} + \,\left( {\dfrac{{ - 1}}{{27}}} \right).27 + 1\\ = \dfrac{1}{9} + ( - 1) + 1\\ = \dfrac{1}{9} + \left[ {( - 1) + 1} \right]\\ = \dfrac{1}{9} + 0\\ = \dfrac{1}{9}\end{array}\)
\(\begin{array}{l}c)\,\,\left( {1,2 - \sqrt {\dfrac{1}{4}} } \right):1\dfrac{1}{{20}} + \left| {\dfrac{3}{4} - 1,25} \right| - {\left( {\dfrac{{ - 3}}{2}} \right)^2}\\\,\, = \,\left( {\dfrac{{12}}{{10}} - \dfrac{1}{2}} \right):\dfrac{{21}}{{20}} + \left| {\dfrac{3}{4} - \dfrac{{125}}{{100}}} \right| - \dfrac{9}{4}\\\,\, = \,\left( {\dfrac{{12}}{{10}} - \dfrac{5}{{10}}} \right):\dfrac{{21}}{{20}} + \left| {\dfrac{3}{4} - \dfrac{5}{4}} \right| - \dfrac{9}{4}\\\,\, = \dfrac{7}{{10}} \cdot \dfrac{{20}}{{21}} + \left| {\dfrac{{ - 2}}{4}} \right| - \dfrac{9}{4}\,\,\\\,\, = \dfrac{{7.10.2}}{{10.7.3}} + \dfrac{2}{4} - \dfrac{9}{4}\\\,\, = \dfrac{2}{3} + \dfrac{2}{4} - \dfrac{9}{4}\\\, = \dfrac{8}{{12}} + \dfrac{6}{{12}} - \dfrac{{27}}{{12}}\\\, = \dfrac{{14}}{{12}} - \dfrac{{27}}{{12}}\\\, = \dfrac{{14 - 27}}{{12}} = \dfrac{{ - 13}}{{12}}\end{array}\)
Câu 6:
\(\begin{array}{l}a)\,\,\dfrac{3}{5}.\left( {2x - \dfrac{1}{3}} \right) + \dfrac{4}{{15}} = \,\dfrac{{12}}{{30}}\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow \dfrac{3}{5}.\left( {2x - \dfrac{1}{3}} \right) = \,\dfrac{{12}}{{30}} - \dfrac{4}{{15}}\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow \dfrac{3}{5}.\left( {2x - \dfrac{1}{3}} \right) = \,\dfrac{6}{{15}} - \dfrac{4}{{15}}\,\,\,\,\\\, \Leftrightarrow \dfrac{3}{5}.\left( {2x - \dfrac{1}{3}} \right) = \,\dfrac{2}{{15}}\,\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow \,2x - \dfrac{1}{3} = \dfrac{2}{{15}}:\dfrac{3}{5}\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow 2x - \dfrac{1}{3} = \dfrac{2}{9}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\, \Leftrightarrow 2x = \dfrac{2}{9} + \dfrac{1}{3}\,\,\,\,\,\,\,\\\, \Leftrightarrow \,2x = \dfrac{5}{9}\\\, \Leftrightarrow x = \dfrac{5}{9}:2\\\, \Leftrightarrow \,x = \dfrac{5}{{18}}\end{array}\)
\(\begin{array}{l}b)\,\,{( - 0,2)^x} = \dfrac{1}{{25}}\,\,\,\,\\ \Leftrightarrow {( - 0,2)^x} = 0,04\,\\ \Leftrightarrow \,{( - 0,2)^x} = {( - 0,2)^2}\,\\ \Leftrightarrow x = 2\,\,\end{array}\)
\(\begin{array}{l}c)\,\,\left| {x - 1} \right| - \dfrac{3}{{12}} = {\left( { - \dfrac{1}{2}} \right)^2}\\ \Leftrightarrow \left| {x - 1} \right| - \dfrac{1}{4} = \dfrac{1}{4}\\ \Leftrightarrow \left| {x - 1} \right| = \dfrac{1}{4} + \dfrac{1}{4}\\ \Leftrightarrow \left| {x - 1} \right| = \dfrac{1}{2}\\ \Rightarrow \left[ \begin{array}{l}x - 1 = \dfrac{1}{2}\\x - 1 = \dfrac{{ - 1}}{2}\end{array} \right.\,\, \Rightarrow \left[ \begin{array}{l}x = \dfrac{1}{2} + 1\\x = \dfrac{{ - 1}}{2} + 1\end{array} \right.\\\,\,\,\, \Rightarrow \left[ \begin{array}{l}x = \dfrac{3}{2}\\x = \dfrac{1}{2}\end{array} \right.\,\end{array}\)
Câu 7
Gọi số sách góp được của ba lớp7A, 7B, 7C lần lượt là \(x,\,\,y,\,\,z\,\,(x,\,\,y,\,\,z > 0,\;\;x,\;y,\;z \in Z)\) (quyển sách)
Theo đề bài số sách góp được của lớp 7A, 7B, 7C tỉ lệ với \(6,\,\,4,\,\,5\)nên \(\dfrac{x}{6} = \dfrac{y}{4} = \dfrac{z}{5}\)
Tổng số sách góp được của lớp 7A với lớp 7B hơn số sách của lớp 7C là \(40\) quyển nên ta có \(x + y - z = 40\).
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{x}{6} = \dfrac{y}{4} = \dfrac{z}{5} = \dfrac{{x + y - z}}{{6 + 4 - 5}} = \dfrac{{40}}{5} = 8\\ \Rightarrow x = 8.6 = 48\\\,\,\,\,\,\,\,y = 8.4 = 32\\\,\,\,\,\,\,z = 8.5 = 40\end{array}\)
Vậy lớp 7A góp được \(48\) quyển sách, lớp 7B góp được \(32\) quyển sách, lớp 7C góp được \(40\) quyển sách.
Câu 8
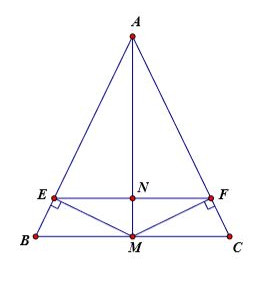
|
GT |
\(\Delta ABC\) có \(AB = AC,\,\,\,M\) là trung điểm của \(BC\). \(ME \bot AB\,\,(E \in AB)\,,\,\,MF \bot AC\,\,(F \in AC)\,\) |
|
KL |
a) \(\Delta AMB = \Delta AMC\). b) \(AE = AF\). c) \(EF\) // \(BC\). |
a) Xét \(\Delta AMB\)và \(\Delta AMC\)ta có:
\(\begin{array}{l}AB = AC\,\,\,(gt)\\AM\;\;chung\\MB = MC\,\,\,(gt)\end{array}\)
Vậy \(\Delta AMB = \Delta AMC\) (c.c.c)
b) Theo phần a) ta có \(\Delta AMB = \Delta AMC\)
\( \Rightarrow \angle MAB = \angle MAC\) (hai góc tương ứng)
Xét hai tam giác vuông \(EMA\) và \(FMA\) ta có:
\(\begin{array}{l}\angle MAB = \angle MAC\;\;\left( {cmt} \right)\\MA\;\;chung\end{array}\)
Vậy \(\Delta EMA = \Delta FMA\) (cạnh huyền – góc nhọn)
Suy ra \(AE = {\rm{AF}}\) (hai cạnh tương ứng).
c) Theo chứng minh ở phần a) ta có \(\Delta AMB = \Delta AMC\)suy ra \(\angle AMB = \angle AMC\) (hai góc tương ứng).
Mà hai góc này ở vị trí kề bù nên \(\angle AMB + \angle AMC = {180^0}\).
\( \Rightarrow \angle AMB = \angle AMC = {90^0}\,\,\, \Rightarrow AM \bot BC\,\,\,\,\,\,\,(1)\)
Gọi \(N\) là giao điểm của \(AM\) và \(EF\). Xét \(\Delta ANE\) và \(\Delta ANF\) ta có:
\(AN\) là cạnh chung
\( \Rightarrow \angle NAE = \angle NAF\) (hai góc tương ứng của \(\Delta AMB = \Delta AMC\))
\(AE = AF\) (theo chứng minh phần b)
Vậy \(\Delta ANE = \Delta ANF\) (c.g.c)
Suy ra \(\angle ANE = \angle ANF\) (hai góc tương ứng).
Mà hai góc này ở vị trí kề bù nên \(\angle ANE + \angle ANF = {180^0}\).
\( \Rightarrow \angle ANE = \angle ANF = {90^0}\,\,\, \Rightarrow EF \bot BC\,\,\,\,\,\,\,(2)\)
Từ \((1)\) và \((2)\) suy ra \(EF//BC\)(đpcm).
Câu 9
\(\dfrac{x}{{y + z + 1}} = \dfrac{y}{{x + z + 1}} = \dfrac{z}{{x + y - 2}} = x + y + z\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
+) Nếu \(x + y + z = 0\) thì từ \((1)\) suy ra \(x = y = z = 0\) .
+) Nếu \(x + y + z \ne 0\). Áp dụng tính chất của dãy tỉ số bằng nhau cho ba tỉ số ta được:
\(\begin{array}{l}\dfrac{x}{{y + z + 1}} = \dfrac{y}{{x + z + 1}} = \dfrac{z}{{x + y - 2}} = x + y + z\,\,\,\,\,\,\,\,\,\\ \Rightarrow x + y + z = \dfrac{{x + y + z}}{{y + z + 1 + x + z + 1 + x + y - 2}} = \dfrac{{x + y + z}}{{2.(x + y + z)}} = \dfrac{1}{2}\\ \Rightarrow x + y = \dfrac{1}{2} - z;\;\;\;x + z = \dfrac{1}{2} - y;\;\;\;y + z = \dfrac{1}{2} - x\end{array}\)
Khi đó \((1)\) trở thành:
\(\begin{array}{l}\;\;\;\;\dfrac{x}{{\dfrac{1}{2} - x + 1}} = \dfrac{y}{{\dfrac{1}{2} - y + 1}} = \dfrac{z}{{\dfrac{1}{2} - z - 2}} = \dfrac{1}{2}\\ \Leftrightarrow \dfrac{x}{{\dfrac{3}{2} - x}} = \dfrac{y}{{\dfrac{3}{2} - y}} = \dfrac{z}{{ - \dfrac{3}{2} - z}} = \dfrac{1}{2}\\ \Rightarrow \left\{ \begin{array}{l}2x = \dfrac{3}{2} - x\\2y = \dfrac{3}{2} - y\\2z = - \dfrac{3}{2} - z\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{1}{2}\\z = - \dfrac{1}{2}\end{array} \right.\end{array}\)
Vậy có hai bộ số \((x,y,z)\) thỏa mãn yêu cầu bài toán: \((0;0;0)\,\,;\,\,\left( {\dfrac{1}{2};\dfrac{1}{2}; - \dfrac{1}{2}} \right)\) .
Xem thêm: Lời giải chi tiết Đề kiểm tra học kì 1 (Đề thi học kì 1) môn Toán 7 tại TimDapAn.com
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề số 11 - Đề kiểm tra học kì 1 - Toán 7 timdapan.com"







