Đề thi học kì 2 Toán 6 - Đề số 8

Đề bài

Phần I: Trắc nghiệm (2 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.

Câu 1: Có ba bao đường: bao thứ nhất nặng 37,6kg; bao thứ hai nặng hơn bao thứ nhât 22,4kg; bao thứ ba nặng bằng \(\dfrac{3}{5}\) bao thứ hai. Cả ba bao đường có khối lượng là:

A. 97,6kg                         B. 96kg                                   C. 73,6kg                                D. 133,6kg

Câu 2: Trong cặp có một số quyển sách là: sách Toán, sách Tiếng Việt và sách Lịch sử. Lấy ngẫu nhiên 1 quyển từ cặp, xem là sách gì rồi trả lại. Lặp lại hoạt động đó 40 ta được kết quả như sau:

A. 0,25                             B. 0,75                                    C. 0,1                                      D. 0,9

Câu 3: Số bộ ba điểm thẳng hàng trong hình vẽ dưới là:

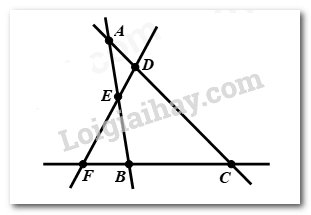
A. \(2\) bộ                        B. \(4\) bộ                               C. \(3\) bộ                               D. \(5\) bộ

Câu 4: Câu nào đúng?

A. Góc lớn hơn góc vuông là góc tù.

B. Góc nhỏ hơn góc bẹt là góc tù.

C. Góc lớn hơn góc nhọn là góc tù.

D. Góc lớn hơn góc vuông, nhỏ hơn góc bẹt là góc tù

Phần II. Tự luận

Bài 1: Thực hiện phép tính (Tính hợp lý nếu có thể).

a) \({\kern 1pt} {\kern 1pt} \dfrac{{ - 10}}{{13}} + \dfrac{5}{{17}} - \dfrac{3}{{13}} + \dfrac{{12}}{{17}} - \dfrac{{11}}{{20}}{\kern 1pt} {\kern 1pt} \)                                  b) \({\kern 1pt} {\kern 1pt} \dfrac{3}{4} + \dfrac{{ - 5}}{6} - \dfrac{{11}}{{ - 12}}\) 

c) \({\kern 1pt} {\kern 1pt} \left( {13\dfrac{4}{9} + 2\dfrac{1}{9}} \right) - 3\dfrac{4}{9}{\kern 1pt} \)                                                  d) \({\kern 1pt} {\kern 1pt} 1,25:\dfrac{{15}}{{20}} + \left( {25\% {\rm{\;}} - \dfrac{5}{6}} \right):4\dfrac{2}{3}\)

Bài 2: Tìm \(x\), biết:

a) \(\dfrac{{29}}{4}x - \dfrac{7}{6} = \dfrac{5}{4}\)                           b) \(2\dfrac{3}{5}:\left( {6x - \dfrac{1}{2}} \right) = \dfrac{{13}}{{10}}\)                              c) \(\dfrac{1}{3}.\left( {3x - 2} \right) + 25\% {\rm{\;}} = {\rm{\;}} - \dfrac{9}{6}\)

Bài 3: Một đoàn học sinh đi thi học sinh giỏi đều đạt giải. Trong đó số học sinh đạt giải nhất chiếm \(\dfrac{1}{2}\) tổng số học sinh; số học sinh đạt giải nhì bằng \(80\% \) số học sinh đạt giải nhất; còn lại có \(5\) học sinh đạt giải ba.

a) Tính tổng số học sinh của đoàn.

b) Tính số học sinh đạt giải nhất, giải nhì và tỉ số phần trăm số học sinh đạt giải từng loại so với tổng số học sinh đi thi.

Bài 4: Vẽ tia \(Ax\).Trên tia \(Ax\) lấy hai điểm \(M\) và \(B\) sao cho \(AM = 4cm,{\kern 1pt} {\kern 1pt} AB = 8cm\).

a) Điểm \(M\) có nằm giữa hai điểm \(A\) và \(B\) không? Vì sao?

b) So sánh \(MA\) và \(MB\).

c) \(M\) có là trung điểm của \(AB\) không? Vì sao?

d) Lấy điểm \(N\) thuộc tia \(Ax\) sao cho \(AN = 12cm\). So sánh \(BM\) và \(BN\).

Bài 5 (0,5 điểm) Tìm các số nguyên n để biểu thức sau nhận giá trị là số nguyên: \(A = \dfrac{{2n - 1}}{{3 - n}}\).

Lời giải

Phần I: Trắc nghiệm

Câu 1

Phương pháp:

Tính khối lượng của bao thứ hai, bao thứ ba, từ đó tính được khối lượng của ba bao đường.

Cách giải:

Bao thứ hai nặng: \(37,6 + 22,4 = 60\left( {kg} \right)\)

Bao thứ ba nặng: \(\dfrac{3}{5}.60 = 36\left( {kg} \right)\)

Cả ba bao đường nặng: \(37,6 + 60 + 36 = 133,6\left( {kg} \right)\)

Chọn D.

Câu 2

Phương pháp:

Áp dụng công thức tính xác suất thực nghiệm: \(\dfrac{{n(A)}}{n}\)

+ Bước 1: Xác định số lần không lấy được sách Tiếng Việt.

+ Bước 2: Tính xác suất thực nghiệm.

Cách giải:

Số lần không lấy được sách Tiếng Việt là: \(14 + 16 = 30\) (lần)

Xác suất thực nghiệm của sự kiện “ Không lấy được sách Tiếng Việt” là: \(\dfrac{{30}}{{40}} = 0,75\)

Chọn B.

Câu 3

Phương pháp:

Sử dụng khái niệm ba điểm thẳng hàng

Cách giải:

Có \(4\) bộ ba điểm thẳng hàng: \(\left( {A,E,B} \right);\left( {F;E,D,} \right);\left( {F,B,C} \right);\left( {A,D,C} \right)\)

Chọn B.

Câu 4

Phương pháp:

Dựa vào tính chất của các góc.

Cách giải:

- Góc lớn hơn góc vuông là góc tù hoặc góc bẹt.

- Góc nhỏ hơn góc bẹt là góc tù, góc vuông hoặc góc nhọn.

- Góc lớn hơn góc nhọn là góc tù, góc vuông hoặc góc bẹt.

- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù

Chọn D.

Phần II: Tự luận

Bài 1

Phương pháp:

Tính giá trị biểu thức theo các quy tắc:

- Biểu thức có dấu ngoặc thì ưu tiên tính trong ngoặc trước, ngoài ngoặc sau.

- Biểu thức có chứa các phép tính cộng, trừ, nhân, chia thì ta thực hiện phép tính nhân, chia trước, phép tính cộng, trừ sau.

Cách giải:

Bài 2

Phương pháp:

Áp dụng quy tắc chuyển vế: Khi chuyển một số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” đổi thành dấu “–” và dấu “–” thành dấu “+”.

Cách giải:

Bài 3

Phương pháp:

a) Quy tắc tìm giá trị phân số của một số cho trước : Muốn tìm \(\dfrac{m}{n}{\kern 1pt} \) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {m,n \in \mathbb{N},{\kern 1pt} {\kern 1pt} n \ne 0} \right).\)

b) Quy tắc tìm một số khi biết giá trị phân số của nó: Muốn tìm một số biết \(\dfrac{m}{n}\) của nó bằng \(a\), ta tính \(a:\dfrac{m}{n}{\kern 1pt} {\kern 1pt} \left( {m,n \in {\mathbb{N}^*}} \right)\).
Cách giải:

a) Đổi \(80\% {\rm{\;}} = \dfrac{4}{5}\).

Phân số chỉ số học sinh đạt giải ba so với số học sinh đạt giải nhất là: \(1 - \dfrac{4}{5} = \dfrac{1}{5}\) (số học sinh đạt giải nhất)

Số học sinh đạt giải nhất là: \(5:\dfrac{1}{5} = 25\) (học sinh)

Tổng số học sinh của đoàn đó là: \(25:\dfrac{1}{2} = 50\) (học sinh)

b) Theo câu ta có số học sinh đạt giải nhất là 25 học sinh.

Số học sinh đạt giải nhì là: \(25.80\% {\rm{\;}} = 20\) (học sinh)

Tỉ số phần trăm số học sinh đạt giải nhất so với tổng số học sinh đi thi là: \(25:50.100\% {\rm{\;}} = 50\% \)

Tỉ số phần trăm số học sinh đạt giải nhì so với tổng số học sinh đi thi là: \(20:50.100\% {\rm{\;}} = 40\% \)

Tỉ số phần trăm số học sinh đạt giải ba so với tổng số học sinh đi thi là: \(5:50.100\% {\rm{\;}} = 10\% \)

Bài 4

Phương pháp:

Dựa vào dấu hiệu nhận biết một điểm nằm giữa hai điểm và tính chất trung điểm của đoạn thẳng.

Cách giải:

a) Trên tia Ax ta có \(AM < AB{\kern 1pt} {\kern 1pt} \left( {4cm < 8cm} \right)\) suy ra điểm \(M\) nằm giữa hai điểm \(A\) và \(B\).

b) Theo câu a, điểm \(M\) nằm giữa hai điểm \(A\) và \(B\) nên ta có: \(AM + MB = AB\)\( \Rightarrow MB = AB - AM = 8 - 4 = 4cm\)

Vậy \(AM = MB = 4cm\).

c) Theo câu a và b ta có: \(M\) nằm giữa hai điểm \(A\) và \(B\) và \(MA = MB\).

Vậy \(M\) là trung điểm của đoạn thẳng AB.

b) Trên tia Ax ta có \(AB < AN{\kern 1pt} {\kern 1pt} \left( {8cm < 12cm} \right)\) suy ra điểm B nằm giữa hai điểm A và N

\(\begin{array}{*{20}{l}}{ \Rightarrow AB + BN = AN}\\{ \Rightarrow BN = AN - AB = 12 - 8 = 4cm}\end{array}\)

Vậy \(MB = \;BN = 4cm\).

Bài 5

Phương pháp:

Phân tích \(A = a + \dfrac{b}{{3 - n}}\), với \(a,\,\,b \in \mathbb{Z}\).

Để \(A \in \mathbb{Z}\) thì \(3 - n \in U\left( b \right)\).

Cách giải:

\(\begin{array}{l}A = \dfrac{{2n - 1}}{{3 - n}} = \dfrac{{2n - 6 + 5}}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{2n - 6}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, = \dfrac{{ - 2\left( { - n + 3} \right)}}{{ - n + 3}} + \dfrac{5}{{ - n + 3}}\\\,\,\,\,\, =  - 2 + \dfrac{5}{{ - n + 3}}\end{array}\)

Để A nhận giá trị nguyên thì \( - 2 + \dfrac{5}{{ - n + 3}} \in \mathbb{Z} \Rightarrow \dfrac{5}{{ - n + 3}} \in \mathbb{Z}\)\( \Rightarrow  - n + 3 \in \left\{ { \pm 1; \pm 5} \right\}\)

Ta có bảng giá trị sau:

Vậy \(n \in \left\{ {2;4; - 2;8} \right\}\).