Đề kiểm tra học kì 2 Toán 10 - Đề số 1 - Kết nối tri thức
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm). Câu 1. Xét hai đại lượng phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì là hàm số của
Đề bài
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
Câu 1. Xét hai đại lượng \(x,y\) phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì \(y\)là hàm số của \(x\)
A. \(y = 2x - 1\).
B. \(\left| y \right| = {x^2}\).
C. \({y^2} = x\).
D. \({y^2} = {x^2} + 1\).
Câu 2. Tập xác định \(D\) của hàm số \(f\left( x \right) = \sqrt {2 - x} + \frac{1}{{\sqrt {x - 1} }}\) là
A. \(D = \left( {1;{\rm{ }}2} \right]\).
B. \(D = \left( { - \infty ;1} \right) \cup \left[ {2; + \infty } \right)\).
C. \(D = \left( { - \infty ;2} \right]\backslash \left\{ 1 \right\}\).
D. \(D = \left( { - \infty ;2} \right]\).
Câu 3. Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Câu 4. Biết đồ thị hàm số \(y = {x^2} + 2x + m\) đi qua điểm \(A( - 1;4)\). Tính \(m\).
A. \(m = 6\).
B. \(m = 7\).
C. \(m = - 25\).
D. \(m = 5\).
Câu 5. Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\). Điều kiện cần và đủ để \(f\left( x \right) < 0,\forall x \in \mathbb{R}\) là
A. \(\left\{ \begin{array}{l}a < 0\\\Delta > 0\end{array} \right.\).
B. \(\left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\).
C. \(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\).
D. \(\left\{ \begin{array}{l}a < 0\\\Delta \ge 0\end{array} \right.\).
Câu 6. Tập nghiệm \(S\) của bất phương trình \( - 2{x^2} + 5x + 7 \le 0\) là
A. \(S = \left( { - \infty ; - 1} \right] \cup \left[ {\frac{7}{2}; + \infty } \right).\)
B. \(S = \left( { - 1;\frac{7}{2}} \right).\)
C. \(S = \left[ { - 1;\frac{7}{2}} \right].\)
D. \(S = \left( { - \infty ; - 1} \right) \cup \left( {\frac{7}{2}; + \infty } \right).\)
Câu 7. Phương trình \(\sqrt {{x^2} - x - 2} = \sqrt {2{x^2} + x - 1} \) có một nghiệm là
A. \(x = 3\).
B. \(x = 2\).
C. \(x = 1\).
D. \(x = - 1\).
Câu 8. Phương trình \(\sqrt {{x^2} - 5x + 4} = - 2x + 2\) có bao nhiêu nghiệm?
A. \(0\).
B. \(2\).
C. \(3\).
D. \(1\).
Câu 9. Trong mặt phẳng toạ độ, cho đường thẳng d có phương trình \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = - 3 + 2t\end{array} \right.\). Tọa độ một véctơ chỉ phương của đường thẳng d là
A. \(\overrightarrow {{n_3}} = (3;2).\)
B. \(\overrightarrow {{n_2}} = (2; - 3)\).
C. \(\overrightarrow {{n_4}} = (2;3)\).
D. \(\overrightarrow {{n_1}} = ( - 2; - 3)\).
Câu 10. Phương trình nào là phương trình tổng quát của đường thẳng?
A. \({y^2} = 3x\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 - 2t}\\{y = 1 + 3t{\rm{ }}}\end{array}} \right.\).
D. \(2x - y - 1 = 0\).
Câu 11. Trong mặt phẳng toạ độ, cho tam giác \(ABC\) có \(A(1;1),B(0;2),C( - 2;6)\). Viết phương trình tổng quát của trung tuyến \(AM\).
A. \(3x - 2y - 1 = 0\).
B. \(3x - 2y + 11 = 0\).
C. \(3x + 2y - 5 = 0\).
D. \(3x + 2y + 5 = 0\).
Câu 12. Trong mặt phẳng toạ độ, cho đường thẳng \(d\) có phương trình \(2x + y - 5 = 0\). Đường thẳng \(d\) song song với đường thẳng có phương trình nào dưới đây?
A. \(x - 2y - 5 = 0\).
B. \( - 2x - y + 5 = 0\).
C. \(2x + y + 5 = 0\).
D. \(x - 2y + 5 = 0\).
Câu 13. Trong mặt phẳng toạ độ, cho hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\). Khi đó góc \(\varphi \) giữa hai đường thẳng được xác định thông qua công thức
A. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
B. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
C. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
D. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
Câu 14. Tính khoảng cách từ điểm \(M\left( {3; - 1} \right)\) đến đường thẳng \(\Delta :4x--3y + 3 = 0\).
A. \(\frac{{18}}{{25}}\).
B. \(\frac{{18}}{5}\).
C. \(\frac{{9\sqrt {10} }}{5}\).
D. \(\frac{9}{5}\).
Câu 15. Trong mặt phẳng tọa độ, phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
B. \({x^2} + {y^2} - 4x + 6y - 12 = 0\).
C. \({x^2} - {y^2} - 2x - 8y + 20 = 0\).
D. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
Câu 16. Tìm tọa độ tâm \(I\) và tính bán kính \(R\) của đường tròn \((C):\,\,{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 9\).
A. \(I( - 2;5),\,\,R = 81.\)
B. \(I(2; - 5),\,\,R = 9.\)
C. \(I(2; - 5),\,\,R = 3.\)
D. \(I( - 2;5),\,\,R = 3.\)
Câu 17. Trong mặt phẳng tọa độ, cho điểm \(I\left( {1;1} \right)\) và đường thẳng \(\left( d \right):3x + 4y - 2 = 0\). Đường tròn tâm \(I\) và tiếp xúc với đường thẳng \(\left( d \right)\) có phương trình
A. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 25\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1\).
Câu 18. Cho đường tròn \(\left( C \right):{x^2} + {y^2} - 2x - 4y - 4 = 0\). Viết phương trình tiếp tuyến của đường tròn \(\left( C \right)\) tại điểm \(A\left( {1;5} \right)\).
A. \(y - 5 = 0\).
B. \(y + 5 = 0\).
C. \(x - 1 = 0\).
D. \(x - y - 6 = 0\).
Câu 19. Trong các phương trình sau, phương trình nào là phương trình chính tắc của hyperbol?
A. \(\frac{{{x^{\rm{2}}}}}{8} + \frac{{{y^{\rm{2}}}}}{4} = 1\).
B. \(\frac{{{x^{\rm{2}}}}}{4} - \frac{{{y^{\rm{2}}}}}{8} = - 1\).
C. \(\frac{{{x^{\rm{2}}}}}{8} + \frac{{{y^{\rm{2}}}}}{4} = - 1\).
D. \(\frac{{{x^{\rm{2}}}}}{8} - \frac{{{y^{\rm{2}}}}}{4} = 1\).
Câu 20. Phương trình chính tắc của \(\left( E \right)\) có độ dài trục lớn bằng \(6\), trục nhỏ bằng \(4\) là
A. \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
B. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\).
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
D. \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{16}} = 1\).
Câu 21. Một tổ có 7 học sinh nữ và 5 học sinh nam. Có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật?
A. \(35\).
B. \(7\).
C. \(5\).
D. \(12\).
Câu 22. Bạn An có 3 kiểu mặt đồng hồ đeo tay và 2 kiểu dây. Hỏi An có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 5.
B. 3.
C. 12.
D. 6.
Câu 23. Từ các chữ số \(1;2;3;5;6;9\) lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau?
A. \(432\). B. \(120\). C. \(240\). D. \(180\).
Câu 24. Cho hai số tự nhiên \(k,\,\,n\) thỏa mãn \(1 \le k \le n\). Số chỉnh hợp chập \(k\) của \(n\) phần tử là
A. \(C_n^k = \frac{{n!}}{{k!(n - k)!}}\).
B. \(A_n^k = \frac{{n!}}{{k!}}\).
C. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
D. \(C_n^k = \frac{{n!}}{{(n - k)!}}\).
Câu 25. Một tổ học sinh có 7 nam và 3 nữ. Trong giờ học thể dục thầy giáo yêu cầu tổ xếp thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp?
A. \(3!\). B. \(3!.4!\). C. \(10!\). D. \(7!.\)
Câu 26. Số tập con có \(9\) phần tử của tập hợp có \(15\) phần tử là
A. \(\frac{{15!}}{{9!}}\).
B. \(5004\).
C. \(5005\).
D. \(A_{15}^9\).
Câu 27. Tổ một của lớp 11/3 có 8 học sinh trong đó có bạn Nam. Hỏi có bao nhiêu cách chọn 4 học sinh trực lớp trong đó phải có Nam?
A. \(35\). B. \(56\). C. \(70.\) D. \(210\).
Câu 28. Tổ \(1\) lớp 11/3 có \(6\) học sinh nam và \(5\) học sinh nữ. Giáo viên chủ nhiệm cần chọn ra \(4\) học sinh của tổ \(1\) để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn \(4\) học sinh trong đó có ít nhất một học sinh nam?
A. \(600\). B. \(25\). C. \(325\). D. \(30\).
Câu 29. Trong khai triển nhị thức Newton của \({\left( {3x - 1} \right)^4}\) có bao nhiêu số hạng?
A. \(6\). B. \(3\). C. \(5\). D. \(4\).
Câu 30. Tung ngẫu nhiên 1 đồng xu cân đối và đồng chất 2 lần. Số phần tử của không gian mẫu \(n\left( \Omega \right)\) bằng
A. \(4\). B. \(8\). C. \(2\). D. \(36\).
Câu 31. Gieo một con súc sắc cân đối và đồng chất. Xác suất để mặt có số chấm chẵn xuất hiện là
A. \(1\).
B. \(\frac{1}{2}\).
C. \(\frac{1}{3}\).
D. \(\frac{1}{6}\).
Câu 32. Một lớp có \(20\) học sinh nam và \(18\) học sinh nữ. Chọn ngẫu nhiên \(1\) học sinh. Tính xác suất chọn được \(1\) học sinh nữ.
A. \(\frac{{10}}{{19}}.\)
B. \(\frac{1}{{18}}.\)
C. \(\frac{9}{{19}}.\)
D. \(\frac{1}{{38}}.\)
Câu 33. Gieo 1 con súc sắc 2 lần. Xác suất của biến cố \(A\) sao cho tổng số chấm xuất hiện trong 2 lần gieo không nhỏ hơn 8 là
A. \(P\left( A \right) = \frac{{13}}{{36}}\).
B. \(P\left( A \right) = \frac{5}{{18}}\).
C. \(P\left( A \right) = \frac{5}{{12}}\).
D. \(P\left( A \right) = \frac{2}{9}\).
Câu 34. Trên kệ có 5 quyển sách toán, 3 quyển sách lý và 4 quyển sách hóa. Lấy ngẫu nhiên 3 quyển. Xác suất để 3 quyển lấy ra có ít nhất 1 quyển sách toán là
A. \(\frac{{41}}{{55}}\).
B. \(\frac{7}{{44}}\).
C. \(\frac{{14}}{{55}}\).
D. \(\frac{{37}}{{44}}\).
Câu 35. Có 2 cái hộp: Hộp thứ nhất có 5 bi xanh và 4 bi đỏ; hộp thứ hai có 4 bi xanh và 3 bi đỏ. Lấy ngẫu nhiên cùng một lúc mỗi hộp 2 bi. Tính xác suất để lấy được đúng 1 bi xanh.
A. \(\frac{{20}}{{63}}\).
B. \(\frac{{41}}{{756}}\).
C. \(\frac{4}{{63}}\).
D. \(\frac{{11}}{{63}}\).
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \sqrt {x - 2m + 1} \) xác định trên khoảng \(\left( {1; + \infty } \right)\).
Câu 37. Trong mặt phẳng tọa độ, cho hai điểm \(A(4; - 1);B( - 2;5).\) Viết phương trình đường tròn đường kính \(AB\).
Câu 38. Một nhóm có 9 học sinh gồm 6 học sinh nam (trong đó có Hiệp) và 3 học sinh nữ. Xếp 9 học sinh đó thành một hàng ngang. Tính xác suất để Hiệp không đứng cạnh bạn nữ nào.
Câu 39. Trong mặt phẳng tọa độ, cho hình chữ nhật \(ABCD\) biết \(BC\) có phương trình \(6x - 7y + 32 = 0\), hình chiếu vuông góc của \(A\) lên \(BD\) là \(K\left( {1;3} \right)\) và đường thẳng \(BD\) đi qua điểm \(H\left( { - 1;\frac{5}{2}} \right)\). Tìm tọa độ điểm \(A\).
---------- HẾT ----------
Lời giải
HƯỚNG DẪN GIẢI CHI TIẾT
THỰC HIỆN: BAN CHYÊN MÔN LOIGIAIHAY.COM
I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).
|
1.A |
2.A |
3.A |
4.D |
5.B |
6.A |
7.C |
|
8.B |
9.A |
10.D |
11.C |
12.C |
13.B |
14.A |
|
15.B |
16.D |
17.C |
18.A |
19.D |
20.C |
21.D |
|
22.D |
23.B |
24.C |
25.C |
26.C |
27.A |
28.C |
|
29.C |
30.A |
31.B |
32.C |
33.C |
34.D |
35.D |
Câu 1. Xét hai đại lượng \(x,y\) phụ thuộc vào nhau theo các hệ thức dưới đây. Trường hợp nào thì \(y\) là hàm số của \(x\)?
A. \(y = 2x - 1\).
B. \(\left| y \right| = {x^2}\).
C. \({y^2} = x\).
D. \({y^2} = {x^2} + 1\).
Phương pháp
Khái niệm hàm số: Nếu với mỗi giá trị của \(x\) thuộc tập hợp số \(D\) có một và chỉ một giá trị tương ứng của \(y\) thuộc tập số thực \(\mathbb{R}\) thì ta có một hàm số.
Lời giải
Ta có \(y = 2x - 1\).
Chọn A.
Câu 2. Tập xác định \(D\) của hàm số \(f\left( x \right) = \sqrt {2 - x} + \frac{1}{{\sqrt {x - 1} }}\) là
A. \(D = \left( {1;{\rm{ }}2} \right]\).
B. \(D = \left( { - \infty ;1} \right) \cup \left[ {2; + \infty } \right)\).
C. \(D = \left( { - \infty ;2} \right]\backslash \left\{ 1 \right\}\).
D. \(D = \left( { - \infty ;2} \right]\).
Phương pháp
-Phân thức xác định khi mẫu thức khác 0
- Căn thức xác định khi biểu thức trong căn lớn hơn bằng 0.
Lời giải
Hàm số xác định khi \(\left\{ \begin{array}{l}2 - x \ge 0\\x - 1 > 0\end{array} \right. \Leftrightarrow 1 < x \le 2\).
Vậy tập xác định của hàm số đã cho \(D = \left( {1;{\rm{ }}2} \right]\).
Chọn A.
Câu 3. Trục đối xứng của đồ thị hàm số \(y = a{x^2} + bx + c\), \((a \ne 0)\) là đường thẳng nào dưới đây?
A. \(x = - \frac{b}{{2a}}.\)
B. \(x = - \frac{c}{{2a}}.\)
C. \(x = - \frac{\Delta }{{4a}}.\)
D. \(x = \frac{b}{{2a}}\).
Phương pháp
Hàm số bậc hai \(y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng có phương trình \(x = - \frac{b}{{2a}}.\)
Lời giải
Hàm số bậc hai \(y = a{x^2} + bx + c\) có trục đối xứng là đường thẳng có phương trình \(x = - \frac{b}{{2a}}.\)
Chọn A.
Câu 4. Biết đồ thị hàm số \(y = {x^2} + 2x + m\) đi qua điểm \(A( - 1;4)\). Tính \(m\).
A. \(m = 6\). B. \(m = 7\). C. \(m = - 25\). D. \(m = 5\).
Phương pháp
Thay tọa độ điểm A vào hàm số để tìm m
Lời giải
Đồ thị hàm số \(y = {x^2} + 2x + m\) đi qua điểm \(A( - 1;4)\) nên \(4 = {\left( { - 1} \right)^2} + 2\left( { - 1} \right) + m \Leftrightarrow m = 5\).
Chọn D.
Câu 5. Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right)\). Điều kiện cần và đủ để \(f\left( x \right) < 0,\forall x \in \mathbb{R}\) là
A. \(\left\{ \begin{array}{l}a < 0\\\Delta > 0\end{array} \right.\).
B. \(\left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\).
C. \(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\).
D. \(\left\{ \begin{array}{l}a < 0\\\Delta \ge 0\end{array} \right.\).
Phương pháp
\(f\left( x \right) = a{x^2} + bx + c < 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\).
Lời giải
\(f\left( x \right) = a{x^2} + bx + c < 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta < 0\end{array} \right.\).
Chọn B.
Câu 6. Tập nghiệm \(S\) của bất phương trình \( - 2{x^2} + 5x + 7 \le 0\) là
A. \(S = \left( { - \infty ; - 1} \right] \cup \left[ {\frac{7}{2}; + \infty } \right).\)
B. \(S = \left( { - 1;\frac{7}{2}} \right).\)
C. \(S = \left[ { - 1;\frac{7}{2}} \right].\)
D. \(S = \left( { - \infty ; - 1} \right) \cup \left( {\frac{7}{2}; + \infty } \right).\)
Phương pháp
Sử dụng dấu của tam thức bậc hai
Lời giải
Ta có :
\( - 2{x^2} + 5x + 7 \le 0 \Leftrightarrow x \le - 1\) hoặc \(x \ge \frac{7}{2}\).
Vậy tập nghiệm của bất phương trình đã cho \(S = \left( { - \infty ; - 1} \right] \cup \left[ {\frac{7}{2}; + \infty } \right).\)
Chọn A.
Câu 7. Phương trình \(\sqrt {{x^2} - x - 2} = \sqrt {2{x^2} + x - 1} \) có một nghiệm là
A. \(x = 3\).
B. \(x = 2\).
C. \(x = 1\).
D. \(x = - 1\).
Phương pháp
Bình phương 2 vế của phương trình
Lời giải
Bình phương 2 vế của phương trình đã cho, ta được
\({x^2} - x - 2 = 2{x^2} + x - 1 \Leftrightarrow {x^2} + 2x + 1 = 0 \Leftrightarrow x = - 1\)
Thử lại ta thấy \(x = - 1\) thỏa mãn.
Vậy tập phương trình đã cho có nghiệm \(x = - 1\).
Chọn D.
Câu 8. Phương trình \(\sqrt {{x^2} - 5x + 4} = - 2x + 2\) có bao nhiêu nghiệm?
A. \(0\). B. \(2\). C. \(3\). D. \(1\).
Phương pháp
Bình phương 2 vế của phương trình
Lời giải
Bình phương 2 vế của phương trình đã cho, ta được
\({x^2} - 5x + 4 = {\left( { - 2x + 2} \right)^2} \Leftrightarrow 3{x^2} - 3x = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 0\end{array} \right.\)
Thử lại ta thấy \(x = - 1\); \(x = 0\) thỏa mãn.
Vậy phương trình đã cho có 2 nghiệm.
Chọn B.
Câu 9. Trong mặt phẳng toạ độ, cho đường thẳng d có phương trình \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = - 3 + 2t\end{array} \right.\). Tọa độ một véctơ chỉ phương của đường thẳng d là
A. \(\overrightarrow {{n_3}} = (3;2).\)
B. \(\overrightarrow {{n_2}} = (2; - 3)\).
C. \(\overrightarrow {{n_4}} = (2;3)\).
D. \(\overrightarrow {{n_1}} = ( - 2; - 3)\).
Phương pháp
Đường thẳng d có phương trình tham số \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.\) có một véctơ chỉ phương \(\overrightarrow u = \left( {a;b} \right)\)
Lời giải
Đường thẳng d có phương trình \(\left\{ \begin{array}{l}x = - 2 + 3t\\y = - 3 + 2t\end{array} \right.\) có một véctơ chỉ phương \(\overrightarrow {{n_3}} = (3;2).\)
Chọn A.
Câu 10. Phương trình nào là phương trình tổng quát của đường thẳng?
A. \({y^2} = 3x\).
B. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x = 3 - 2t}\\{y = 1 + 3t{\rm{ }}}\end{array}} \right.\).
D. \(2x - y - 1 = 0\).
Phương pháp
Phương trình tổng quát của đường thẳng có dạng: \(ax + by + c = 0\)
Lời giải
Ta có \({y^2} = 3x\) là phương trình parabol;
\(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) là phương trình elip;
\(\left\{ {\begin{array}{*{20}{l}}{x = 3 - 2t}\\{y = 1 + 3t{\rm{ }}}\end{array}} \right.\) là phương trình tham số của đường thẳng.
Chọn D.
Câu 11. Trong mặt phẳng toạ độ, cho tam giác \(ABC\) có \(A(1;1),B(0;2),C( - 2;6)\). Viết phương trình tổng quát của trung tuyến \(AM\).
A. \(3x - 2y - 1 = 0\).
B. \(3x - 2y + 11 = 0\).
C. \(3x + 2y - 5 = 0\).
D. \(3x + 2y + 5 = 0\).
Phương pháp
Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
\(M\) là trung điểm của \(BC\) nên \(M\left( { - 1;4} \right)\).
Đường trung tuyến \(AM\) đi qua \(A,M\) nên nhận \(\overrightarrow {AM} = \left( { - 2;3} \right)\) làm véctơ chỉ phương. Suy ra \(AM\) có một véctơ pháp tuyến \(\overrightarrow n = \left( {3;2} \right)\).
Vậy \(AM\) có phương trình tổng quát \(3\left( {x - 1} \right) + 2\left( {y - 1} \right) = 0\) hay \(3x + 2y - 5 = 0\).
Chọn C.
Câu 12. Trong mặt phẳng toạ độ, cho đường thẳng \(d\) có phương trình \(2x + y - 5 = 0\). Đường thẳng \(d\) song song với đường thẳng có phương trình nào dưới đây?
A. \(x - 2y - 5 = 0\).
B. \( - 2x - y + 5 = 0\).
C. \(2x + y + 5 = 0\).
D. \(x - 2y + 5 = 0\).
Phương pháp
Sử dụng công thức vị trí tương đối của hai đường thẳng.
Lời giải
Ta có \(\left\{ \begin{array}{l}2x + y - 5 = 0\\2x + y + 5 = 0\end{array} \right.\) vô nghiệm nên đường thẳng \(d\) có phương trình \(2x + y - 5 = 0\) song song với đường thẳng có phương trình \(2x + y + 5 = 0\).
Chọn C.
Câu 13. Trong mặt phẳng toạ độ, cho hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\). Khi đó góc \(\varphi \) giữa hai đường thẳng được xác định thông qua công thức
A. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
B. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
C. \(\cos \varphi = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
D. \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} + \sqrt {a_2^2 + b_2^2} }}\).
Phương pháp
Góc \(\varphi \) giữa hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\) được tính theo công thức \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
Lời giải
Góc \(\varphi \) giữa hai đường thẳng \({d_1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({d_2}:{a_2}x + {b_2}y + {c_2} = 0\) được tính theo công thức \(\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\).
Chọn B.
Câu 14. Tính khoảng cách từ điểm \(M\left( {3; - 1} \right)\) đến đường thẳng \(\Delta :4x--3y + 3 = 0\).
A. \(\frac{{18}}{{25}}\).
B. \(\frac{{18}}{5}\).
C. \(\frac{{9\sqrt {10} }}{5}\).
D. \(\frac{9}{5}\).
Phương pháp
Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Khoảng cách từ điểm \(M\left( {3; - 1} \right)\) đến đường thẳng \(\Delta :4x--3y + 3 = 0\)
\(d\left( {M,\Delta } \right) = \frac{{\left| {4.3 - 3\left( { - 1} \right) + 3} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{18}}{5}\)
Chọn A.
Câu 15. Trong mặt phẳng tọa độ, phương trình nào sau đây là phương trình của một đường tròn?
A. \({x^2} + 2{y^2} - 4x - 8y + 1 = 0\).
B. \({x^2} + {y^2} - 4x + 6y - 12 = 0\).
C. \({x^2} - {y^2} - 2x - 8y + 20 = 0\).
D. \(4{x^2} + {y^2} - 10x - 6y - 2 = 0\).
Phương pháp
Phương trình có dạng \({x^2} + {y^2} - 2ax - 2by + c = 0\) với \({a^2} + {b^2} - c > 0\) là phương trình của một đường tròn.
Lời giải
Phương trình của một đường tròn là \({x^2} + {y^2} - 4x + 6y - 12 = 0\)
Chọn B.
Câu 16. Tìm tọa độ tâm \(I\) và tính bán kính \(R\) của đường tròn \((C):\,\,{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 9\).
A. \(I( - 2;5),\,\,R = 81.\)
B. \(I(2; - 5),\,\,R = 9.\)
C. \(I(2; - 5),\,\,R = 3.\)
D. \(I( - 2;5),\,\,R = 3.\)
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
Đường tròn \((C):\,\,{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) có tâm \(I\left( {a;b} \right)\), bán kính \(R\) nên đường tròn \((C):\,\,{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 9\) có tâm \(I\left( { - 2;5} \right)\), bán kính \(R = 3\).
Chọn D.
Câu 17. Trong mặt phẳng tọa độ, cho điểm \(I\left( {1;1} \right)\) và đường thẳng \(\left( d \right):3x + 4y - 2 = 0\). Đường tròn tâm \(I\) và tiếp xúc với đường thẳng \(\left( d \right)\) có phương trình
A. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\).
B. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 25\).
C. \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
D. \({\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 1\).
Phương pháp
- Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)
- Khoảng cách từ điểm \(M({x_0};{y_0})\) đến đường thẳng \(\Delta :{\rm{ }}ax + by + c = 0\) là: \(d(M,\Delta ) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)
Lời giải
Đường tròn tâm \(I\left( {1;1} \right)\), tiếp xúc với đường thẳng \(\left( d \right)\) có bán kính \(R = d\left( {I,d} \right) = \frac{{\left| {3.1 + 4.1 - 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 1\) nên có phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\).
Chọn C.
Câu 18. Cho đường tròn \(\left( C \right):{x^2} + {y^2} - 2x - 4y - 4 = 0\). Viết phương trình tiếp tuyến của đường tròn \(\left( C \right)\) tại điểm \(A\left( {1;5} \right)\).
A. \(y - 5 = 0\).
B. \(y + 5 = 0\).
C. \(x - 1 = 0\).
D. \(x - y - 6 = 0\).
Phương pháp
Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
Đường tròn \(\left( C \right)\) có tâm \(I\left( {1;2} \right)\). Tiếp tuyến của \(\left( C \right)\) tại điểm \(A\left( {1;5} \right)\) có vectơ pháp tuyến \(\overrightarrow {IA} = \left( {0;3} \right)\), nên có phương trình \(0\left( {x - 1} \right) + 3\left( {y - 5} \right) = 0 \Leftrightarrow y - 5 = 0\).
Chọn A.
Câu 19. Trong các phương trình sau, phương trình nào là phương trình chính tắc của hyperbol?
A. \(\frac{{{x^{\rm{2}}}}}{8} + \frac{{{y^{\rm{2}}}}}{4} = 1\).
B. \(\frac{{{x^{\rm{2}}}}}{4} - \frac{{{y^{\rm{2}}}}}{8} = - 1\).
C. \(\frac{{{x^{\rm{2}}}}}{8} + \frac{{{y^{\rm{2}}}}}{4} = - 1\).
D. \(\frac{{{x^{\rm{2}}}}}{8} - \frac{{{y^{\rm{2}}}}}{4} = 1\).
Phương pháp
Phương trình \(\frac{{{x^{\rm{2}}}}}{{{a^2}}} - \frac{{{y^{\rm{2}}}}}{{{b^2}}} = 1\), với \(a,b > 0\) là phương trình chính tắc của hyperbol.
Lời giải
Phương trình \(\frac{{{x^{\rm{2}}}}}{8} - \frac{{{y^{\rm{2}}}}}{4} = 1\) là phương trình chính tắc của hyperbol.
Chọn D.
Câu 20. Phương trình chính tắc của \(\left( E \right)\) có độ dài trục lớn bằng \(6\), trục nhỏ bằng \(4\) là
A. \(\frac{{{x^2}}}{9} - \frac{{{y^2}}}{4} = 1\).
B. \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{16}} = 1\).
C. \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
D. \(\frac{{{x^2}}}{{36}} - \frac{{{y^2}}}{{16}} = 1\).
Phương pháp
Phương trình \(\frac{{{x^{\rm{2}}}}}{{{a^2}}} + \frac{{{y^{\rm{2}}}}}{{{b^2}}} = 1\), với \(a,b > 0\) là phương trình chính tắc của elip (E)
Lời giải
\(\left( E \right)\) có độ dài trục lớn bằng \(6\), trục nhỏ bằng \(4\) \( \Rightarrow \left\{ \begin{array}{l}2a = 6\\2b = 4\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 3\\b = 2\end{array} \right.\)
Vậy \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\).
Chọn C.
Câu 21. Một tổ có 7 học sinh nữ và 5 học sinh nam. Có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật?
A. \(35\).
B. \(7\).
C. \(5\).
D. \(12\).
Phương pháp
Áp dụng quy tắc cộng
Lời giải
Chọn 1 học sinh nữ có 7 cách.
Chọn 1 học sinh nam có 5 cách.
Theo quy tắc cộng, ta có 7 + 5 = 12 cách.
Chọn D.
Câu 22. Bạn An có 3 kiểu mặt đồng hồ đeo tay và 2 kiểu dây. Hỏi An có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 5. B. 3. C. 12. D. 6.
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Chọn 1 mặt đồng hồ có 3 cách.
Chọn 1 dây có 2 cách.
Theo quy tắc nhân, ta có 3.2 = 6 cách.
Chọn D.
Câu 23. Từ các chữ số \(1;2;3;5;6;9\) lập được bao nhiêu số tự nhiên chẵn gồm 4 chữ số đôi một khác nhau?
A. \(432\). B. \(120\). C. \(240\). D. \(180\).
Phương pháp
Áp dụng quy tắc nhân
Lời giải
Gọi số cần lập là \(\overline {abcd} \).
Chọn \(d\) có 2 cách; chọn \(a\) có 5 cách; chọn \(b\) có 4 cách; chọn \(c\) có 3 cách.
Theo quy tắc nhân, ta có 2.5.4.3 = 120 số cần lập.
Chọn B.
Câu 24. Cho hai số tự nhiên \(k,\,\,n\) thỏa mãn \(1 \le k \le n\). Số chỉnh hợp chập \(k\) của \(n\) phần tử là
A. \(C_n^k = \frac{{n!}}{{k!(n - k)!}}\).
B. \(A_n^k = \frac{{n!}}{{k!}}\).
C. \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
D. \(C_n^k = \frac{{n!}}{{(n - k)!}}\).
Phương pháp
Số chỉnh hợp chập \(k\) của \(n\) phần tử được tính theo công thức \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
Lời giải
Số chỉnh hợp chập \(k\) của \(n\) phần tử được tính theo công thức \(A_n^k = \frac{{n!}}{{\left( {n - k} \right)!}}\).
Chọn C.
Câu 25. Một tổ học sinh có 7 nam và 3 nữ. Trong giờ học thể dục thầy giáo yêu cầu tổ xếp thành một hàng dọc. Hỏi có bao nhiêu cách sắp xếp?
A. \(3!\). B. \(3!.4!\). C. \(10!\). D. \(7!.\)
Phương pháp
Áp dụng công thức hoán vị
Lời giải
Sắp xếp 10 học sinh thành một dọc có \(10!\) cách xếp.
Chọn C.
Câu 26. Số tập con có \(9\) phần tử của tập hợp có \(15\) phần tử là
A. \(\frac{{15!}}{{9!}}\).
B. \(5004\).
C. \(5005\).
D. \(A_{15}^9\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
Số tập con có \(9\) phần tử của tập hợp có \(15\) phần tử là \(C_{15}^9 = 5005\).
Chọn C.
Câu 27. Tổ một của lớp 11/3 có 8 học sinh trong đó có bạn Nam. Hỏi có bao nhiêu cách chọn 4 học sinh trực lớp trong đó phải có Nam?
A. \(35\). B. \(56\). C. \(70.\) D. \(210\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
+ Chọn Nam: có 1 cách
+ Chọn thêm 3 học sinh từ 7 học sinh còn lại: có \(C_7^3 = 35\) cách.
Vậy có \(1.C_7^3 = 35\) cách.
Chọn A.
Câu 28. Tổ \(1\) lớp 11/3 có \(6\) học sinh nam và \(5\) học sinh nữ. Giáo viên chủ nhiệm cần chọn ra \(4\) học sinh của tổ \(1\) để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn \(4\) học sinh trong đó có ít nhất một học sinh nam?
A. \(600\). B. \(25\). C. \(325\). D. \(30\).
Phương pháp
Áp dụng công thức tổ hợp
Lời giải
+ Chọn 4 học sinh bất kỳ từ 11 học sinh: có \(C_{11}^4 = 330\) cách.
+ Chọn 4 học sinh đều là nữ có \(C_5^4 = 5\) cách.
Vậy có \(330 - 5 = 325\) cách chọn \(4\) học sinh trong đó có ít nhất một học sinh nam.
Chọn C.
Câu 29. Trong khai triển nhị thức Newton của \({\left( {3x - 1} \right)^4}\) có bao nhiêu số hạng?
A. \(6\). B. \(3\). C. \(5\). D. \(4\).
Phương pháp
Sử dụng công thức khai triển nhị thức Newton
Lời giải
Trong khai triển nhị thức Newton của \({\left( {3x - 1} \right)^4}\) có \(4 + 1 = 5\) số hạng.
Chọn C.
Câu 30. Tung ngẫu nhiên 1 đồng xu cân đối và đồng chất 2 lần. Số phần tử của không gian mẫu \(n\left( \Omega \right)\) bằng
A. \(4\). B. \(8\). C. \(2\). D. \(36\).
Phương pháp
Sử dụng quy tắc đếm
Lời giải
\(\Omega = \left\{ {{\rm{SS}}{\rm{,SN}}{\rm{,NS}}{\rm{,NN}}} \right\}\) \( \Rightarrow n\left( \Omega \right) = 4\).
Chọn A.
Câu 31. Gieo một con súc sắc cân đối và đồng chất. Xác suất để mặt có số chấm chẵn xuất hiện là
A. \(1\).
B. \(\frac{1}{2}\).
C. \(\frac{1}{3}\).
D. \(\frac{1}{6}\).
Phương pháp
Công thức tính xác suất
Lời giải
\(\Omega = \left\{ {{\rm{1;2;3;4;5;6}}} \right\}\) \( \Rightarrow n\left( \Omega \right) = 6\).
Gọi \(A\) là biến cố: “mặt có số chấm chẵn xuất hiện” \( \Rightarrow A = \left\{ {2;4;6} \right\} \Rightarrow n\left( A \right) = 3\).
Xác suất để \(A\) xảy ra: \(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{6} = \frac{1}{2}\).
Chọn B.
Câu 32. Một lớp có \(20\) học sinh nam và \(22\) học sinh nữ. Chọn ngẫu nhiên \(1\) học sinh. Tính xác suất chọn được \(1\) học sinh nữ.
A. \(\frac{1}{{22}}.\)
B. \(\frac{1}{{20}}.\)
C. \(\frac{{11}}{{21}}.\)
D. \(\frac{{10}}{{21}}.\)
Phương pháp
Công thức tính xác suất
Lời giải
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = 20 + 22 = 42\).
Gọi \(A\) là biến cố: “chọn được \(1\) học sinh nữ” \( \Rightarrow n\left( A \right) = 22\).
Xác suất để \(A\) xảy ra: \(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{22}}{{42}} = \frac{{11}}{{21}}\).
Chọn C.
Câu 33. Gieo 1 con súc sắc 2 lần. Xác suất của biến cố \(A\) sao cho tổng số chấm xuất hiện trong 2 lần gieo không nhỏ hơn 8 là
A. \(P\left( A \right) = \frac{{13}}{{36}}\).
B. \(P\left( A \right) = \frac{5}{{18}}\).
C. \(P\left( A \right) = \frac{5}{{12}}\).
D. \(P\left( A \right) = \frac{2}{9}\).
Phương pháp
Công thức tính xác suất
Lời giải
\(n\left( \Omega \right) = 36\).
\(A = \{ \left( {2;6} \right),\left( {3;5} \right),\left( {3;6} \right),\left( {4;4} \right),\left( {4;5} \right),\left( {4;6} \right),\left( {5;3} \right),\left( {5;4} \right),\left( {5;5} \right),\left( {5;6} \right)\\\left( {6;2} \right),\left( {6;3} \right),\left( {6;4} \right),\left( {6;5} \right),\left( {6;6} \right)\} \)
\( \Rightarrow n\left( A \right) = 15\).
Xác suất để \(A\) xảy ra: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{15}}{{36}} = \frac{5}{{12}}\).
Chọn C.
Câu 34. Trên kệ có 5 quyển sách toán, 3 quyển sách lý và 4 quyển sách hóa. Lấy ngẫu nhiên 3 quyển. Xác suất để 3 quyển lấy ra có ít nhất 1 quyển sách toán là
A. \(\frac{{41}}{{55}}\).
B. \(\frac{7}{{44}}\).
C. \(\frac{{14}}{{55}}\).
D. \(\frac{{37}}{{44}}\).
Phương pháp
Công thức tính xác suất
Lời giải
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_{12}^3 = 220\).
Gọi \(A\) là biến cố: “có ít nhất một quyển sách Toán” \( \Rightarrow n\left( A \right) = 5.C_7^2 + C_5^2.7 + C_5^3 = 185\).
Xác suất để \(A\) xảy ra: \(\frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{185}}{{220}} = \frac{{37}}{{44}}\).
Chọn D.
Câu 35. Có 2 cái hộp: Hộp thứ nhất có 5 bi xanh và 4 bi đỏ; hộp thứ hai có 4 bi xanh và 3 bi đỏ. Lấy ngẫu nhiên cùng một lúc mỗi hộp 2 bi. Tính xác suất để lấy được đúng 1 bi xanh.
A. \(\frac{{20}}{{63}}\).
B. \(\frac{{41}}{{756}}\).
C. \(\frac{4}{{63}}\).
D. \(\frac{{11}}{{63}}\).
Phương pháp
Công thức tính xác suất
Lời giải
Số phần tử của không gian mẫu: \(n\left( \Omega \right) = C_9^2.C_7^2\).
Gọi \(A\) là biến cố: “lấy được đúng 1 bi xanh”.
+ Lấy đúng 1 viên bi xanh ở hộp thứ nhất: có \(5.4.C_3^2\) cách.
+ Lấy đúng 1 viên bi xanh ở hộp thứ hai: có \(4.3.C_4^2\) cách.
\( \Rightarrow n\left( A \right) = 5.4.C_3^2 + 4.3.C_4^2\).
Xác suất để \(A\) xảy ra: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{5.4.C_3^2 + 4.3.C_4^2}}{{C_9^2.C_7^2}} = \frac{{11}}{{63}}\).
Chọn D.
II. TỰ LUẬN (04 câu – 3,0 điểm)
Câu 36. Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = \sqrt {x - 2m + 1} \) xác định trên khoảng \(\left( {1; + \infty } \right)\).
Phương pháp
Căn thức xác định khi biểu thức trong căn lớn hơn bằng 0
Lời giải
+ Hàm số xác định khi \(x - 2m + 1 \ge 0 \Leftrightarrow x \ge 2m - 1\).
\( \Rightarrow \) tập xác định của hàm số \(D = \left[ {2m - 1; + \infty } \right)\).
+ Hàm số xác định trên khoảng \(\left( {1; + \infty } \right)\) khi \(\left( {1; + \infty } \right) \subset \left[ {2m - 1; + \infty } \right) \Leftrightarrow 2m - 1 \le 1 \Leftrightarrow m \le 1\).
Câu 37. Trong mặt phẳng tọa độ, cho hai điểm \(A(4; - 1);B( - 2;5).\) Viết phương trình đường tròn đường kính \(AB\).
Phương pháp
Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : \({(x - a)^2} + {(y - b)^2} = {R^2}\)
Lời giải
+ Gọi \(I\) là trung điểm \(AB \Rightarrow I\left( {1;2} \right)\).
+ Đường tròn đường kính \(AB\) có tâm \(I\left( {1;2} \right)\), bán kính \(R = \frac{{AB}}{2} = \frac{{\sqrt {{{\left( { - 2 - 4} \right)}^2} + {{\left( {5 + 1} \right)}^2}} }}{2} = 3\sqrt 2 \) nên có phương trình: \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 18\).
Câu 38. Một nhóm có 9 học sinh gồm 6 học sinh nam (trong đó có Hiệp) và 3 học sinh nữ. Xếp 9 học sinh đó thành một hàng ngang. Tính xác suất để Hiệp không đứng cạnh bạn nữ nào.
Phương pháp
Công thức tính xác suất
Lời giải
Số phần tử của không gian mẫu là: \(n\left( \Omega \right) = 9!\).
Gọi A là biến cố: “Hiệp không đứng cạnh bạn nữ nào”.
Có 2 trường hợp:
* Trường hợp 1: Hiệp đứng đầu hoặc cuối hàng.
+ Xếp chỗ ngồi cho Hiệp, có 2 cách.
+ Chọn 3 chỗ từ 7 chỗ không kề với Hiệp và xếp cho 3 bạn nữ, có \(A_7^3\) cách.
+ Xếp chỗ ngồi cho 5 bạn nam còn lại, có \(5!\) cách.
Suy ra trường hợp 1 có: 2.\(A_7^3\). \(5!\) = 50400 cách xếp.
* Trường hợp 2: Hiệp không đứng đầu hoặc cuối hàng.
+ Xếp chỗ ngồi cho Hiệp, có 7 cách.
+ Chọn 3 chỗ từ 6 chỗ không kề với Hiệp và xếp cho 3 bạn nữ, có \(A_6^3\) cách.
+ Xếp chỗ ngồi cho 5 bạn nam còn lại, có \(5!\) cách.
Suy ra trường hợp 2 có 7.\(A_6^3\).\(5!\) = 100800 cách xếp.
Khi đó, ta có số phần tử biến cố A: \(n\left( A \right) = 50400 + 100800 = 151200\).
Vậy xác suất cần tính: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{{12}}\).
Câu 39. Trong mặt phẳng tọa độ, cho hình chữ nhật \(ABCD\) biết \(BC\) có phương trình \(6x - 7y + 32 = 0\), hình chiếu vuông góc của \(A\) lên \(BD\) là \(K\left( {1;3} \right)\) và đường thẳng \(BD\) đi qua điểm \(H\left( { - 1;\frac{5}{2}} \right)\). Viết phương trình đường thẳng \(BD\) và tìm tọa độ điểm \(A\).
Phương pháp
Phương trình tổng quát của đường thẳng đi qua điểm \(A\left( {{x_0},{y_0}} \right)\) và nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vecto pháp tuyến là : \(d:a(x - {x_0}) + b(y - {y_0}) = 0\)
Lời giải
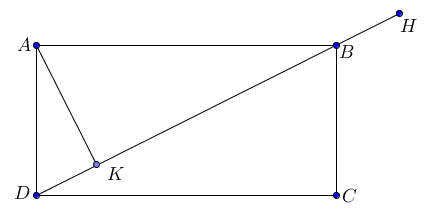
+ Đường thẳng \(BD\) đi qua 2 điểm \(H,K\) nên nhận vectơ \(\overrightarrow {HK} = \left( {2;\frac{1}{2}} \right)\) làm vectơ chỉ phương
\( \Rightarrow BD\) có 1 vectơ pháp tuyến \(\overrightarrow n = \left( {1; - 4} \right)\) nên \(BD\) có phương trình \(x - 4y + 11 = 0\).
+ \(B = BC \cap BD \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}6x - 7y + 32 = 0\\x - 4y + 11 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = 2\end{array} \right.\).
Suy ra \(B\left( { - 3;2} \right)\).
+ Đường thẳng \(AB\) vuông góc với \(BC\) nên \(AB\) có dạng \(7x + 6y + c = 0\).
\(AB\) đi qua điểm \(B\left( { - 3;2} \right)\) nên \(7\left( { - 3} \right) + 6.2 + c = 0 \Leftrightarrow c = 9\).
Vậy \(AB\) có phương trình\(7x + 6y + 9 = 0\)
+ Đường thẳng \(AK\) đi qua điểm \(K\) và vuông góc với \(BD\) nên có phương trình \(4x + y - 7 = 0\).
+ \(A = AB \cap AK \Rightarrow A\left( {3; - 5} \right)\).
---------- HẾT ----------
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra học kì 2 Toán 10 - Đề số 1 - Kết nối tri thức timdapan.com"







