Đề kiểm tra giữa kì 2 Toán 10 - đề số 6 có lời giải chi tiết

Đề bài

Câu 1 (5,0 điểm): Giải các bất phương trình sau:

a) \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)   

b) \(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\)     

c) \({\left( {\left| {x - 3} \right| - 1} \right)^2} > {x^2}\)

Câu 2 (1,5 điểm): Tìm \(m\) để bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý.

Câu 3 (2,0 điểm): Giải hệ bất phương trình: \(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\).

Câu 4 (1,5 điểm): Tìm \(m\) để phương trình \(m{x^2} - 2\left( {m + 1} \right)x + 2 = 0\) có nghiệm âm.

Lời giải chi tiết

Câu 1 (VD) - Bất phương trình

Phương pháp:

a) Tìm ĐKXĐ. Lập bảng xét dấu để tìm tập nghiệm của bất phương trình.

b) Quy đồng và áp dụng: Nếu \(\dfrac{a}{b} < 0\) và \(a > 0\) thì \(b < 0\).

c) Phá dấu giá trị tuyệt đối, giải các bất phương trình nhận được và kết luận tập nhiệm: \(\left| a \right| = \left\{ \begin{array}{l}a\,\,{\mathop{\rm khi}\nolimits} \,\,a \ge 0\\ - a\,\,{\mathop{\rm khi}\nolimits} \,\,a < 0\end{array} \right.\)

Cách giải:

Giải các bất phương trình sau:

a) \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)

\(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\)

ĐKXĐ: \(5 - {x^2} \ne 0 \Leftrightarrow x \ne  \pm \sqrt 5 \)

Ta có bảng xét dấu:

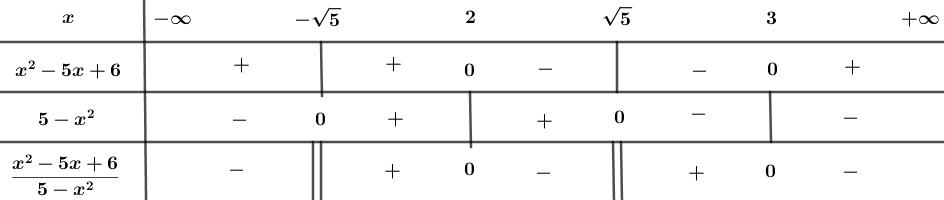
Để \(\dfrac{{{x^2} - 5x + 6}}{{5 - {x^2}}} \ge 0\) thì \(x \in \left( { - \sqrt 5 ;\,\,2} \right] \cup \left( {\sqrt 5 ;\,\,3} \right]\)

Vậy bất phương trình có tập nghiệm \(S = \left( { - \sqrt 5 ;\,\,2} \right] \cup \left( {\sqrt 5 ;\,\,3} \right]\).

b) \(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\)

\(\dfrac{1}{{x - 2}} - \dfrac{1}{{x - 1}} < 0\)                                                      ĐKXĐ: \(x \ne 1;\,\,x \ne 2\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{\left( {x - 1} \right) - \left( {x - 2} \right)}}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\\ \Leftrightarrow \dfrac{{x - 1 - x + 2}}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\\ \Leftrightarrow \dfrac{1}{{\left( {x - 1} \right).\left( {x - 2} \right)}} < 0\end{array}\)

\(\begin{array}{l} \Leftrightarrow \left( {x - 1} \right).\left( {x - 2} \right) < 0\,\,\,\left( {{\rm{vì }}\,\,1 > 0} \right)\\ \Leftrightarrow 1 < x < 2\end{array}\)

Vậy bất phương trình có tập nghiệm \(S = \left( {1;\,\,2} \right)\).

c) \({\left( {\left| {x - 3} \right| - 1} \right)^2} > {x^2}\)

TH1: \(x - 3 \ge 0 \Leftrightarrow x \ge 3\)

Bất phương trình \( \Leftrightarrow {\left( {x - 4} \right)^2} > {x^2}\)

\( \Leftrightarrow {x^2} - 8x + 16 > {x^2}\)

\( \Leftrightarrow  - 8x + 16 > 0\)

\( \Leftrightarrow x < 2\)

Mà \(x \ge 3 \Rightarrow x \in \left\{ \emptyset  \right\}\).

TH2: \(x - 3 < 0 \Leftrightarrow x < 3\)

Bất phương trình \( \Leftrightarrow {\left( {2 - x} \right)^2} > {x^2}\)

\( \Leftrightarrow 4 - 4x + {x^2} > {x^2}\)

\( \Leftrightarrow 4 - 4x > 0\)

\( \Leftrightarrow x < 1\)

Mà \(x < 3 \Rightarrow x < 1\).

Kết hợp cả hai trường hợp ta được tập nghiệm của bất phương trình là: \(S = \left( { - \infty ;\,\,1} \right)\)

Câu 2 (VD) - Bất phương trình

Phương pháp:

Áp dụng: \(f\left( x \right) = {a^2}x + bx + c \ge 0,\,\,\forall x \in \mathbb{R}\)\( \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\)

Cách giải:

Tìm \(m\) để bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý.

Bất phương trình \({x^2} - 2\left( {m - \dfrac{2}{3}} \right)x - m + \dfrac{{20}}{3} \ge 0\) có nghiệm tùy ý khi và chỉ khi \(\left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

+) \(a = 1 > 0\) luôn đúng

+) \(\Delta  \le 0\)

\(\begin{array}{l}\Delta  \le 0 \Leftrightarrow 4{\left( {m - \dfrac{2}{3}} \right)^2} - 4.1.\left( { - m + \dfrac{{20}}{3}} \right) \le 0\\\, \Leftrightarrow 4\left( {{m^2} - \dfrac{4}{3}m + \dfrac{4}{9}} \right) + 4m - \dfrac{{80}}{3} \le 0\\\, \Leftrightarrow 4{m^2} - \dfrac{{16}}{3}m + \dfrac{{16}}{9} + 4m - \dfrac{{80}}{3} \le 0\\\, \Leftrightarrow 4{m^2} - \dfrac{4}{3}m - \dfrac{{224}}{9} \le 0\\\, \Leftrightarrow  - \dfrac{7}{3} \le m \le \dfrac{8}{3}\end{array}\)

Vậy \( - \dfrac{7}{3} \le m \le \dfrac{8}{3}\).

Câu 3 (VD) - Bất phương trình và hệ bất phương trình một ẩn

Phương pháp:

Giải từng bất phương trình sau đó kết hợp nghiệm.

Cách giải:

Giải hệ bất phương trình: \(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\).

 \(\left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{\left( {x + 1} \right)^2} - 16 > 0\end{array} \right.\)  

ĐKXĐ: \(4x - 1 \ne 0 \Leftrightarrow x \ne \dfrac{1}{4}\)

\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{x^2} + 2x + 1 - 16 > 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{2 - 3x}}{{4x - 1}} \le 0\\{x^2} + 2x - 15 > 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}\left\{ \begin{array}{l}2 - 3x \ge 0\\4x - 1 < 0\end{array} \right.\\\left\{ \begin{array}{l}2 - 3x \le 0\\4x - 1 > 0\end{array} \right.\end{array} \right.\\\left[ \begin{array}{l}x <  - 5\\x > 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x < \dfrac{1}{4}\\x \ge \dfrac{2}{3}\end{array} \right.\\\left[ \begin{array}{l}x <  - 5\\x > 3\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x <  - 5\\x > 3\end{array} \right.\)

Vậy hệ bất phương trình có tập nghiệm \(S = \left( { - \infty ;\,\, - 5} \right) \cup \left( {3;\,\, + \infty } \right)\).

Câu 4 (VDC) - Phương trình quy về phương trình bậc hai

Phương pháp:

Xác định điều kiện của \(m\) để phương trình có hai nghiệm trái dấu và hai nghiệm âm.

Cách giải:

Tìm \(m\) để phương trình \(m{x^2} - 2\left( {m + 1} \right)x + 2 = 0\,\,\,\left( 1 \right)\) có nghiệm âm.

+) \(m = 0\): PT \(\left( 1 \right)\) trở thành: \( - 2x + 2 = 0\)\( \Leftrightarrow x = 1 > 0\) (không thỏa mãn)

+) \(m \ne 0\)

\(\Delta  = 4{\left( {m + 1} \right)^2} - 4.m.2\)\( = 4{m^2} + 4 > 0\) với mọi \(m\)
\( \Rightarrow \) Phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt với \(m \ne 0\).

PT \(\left( 1 \right)\) có \(1\) nghiệm âm \( \Leftrightarrow \)PT \(\left( 1 \right)\) có hai nghiệm trái dấu \( \Leftrightarrow \)\(ac < 0 \Leftrightarrow 2m < 0\)\( \Leftrightarrow m < 0\).

PT \(\left( 1 \right)\) có \(2\) nghiệm âm \( \Leftrightarrow \left\{ \begin{array}{l}P > 0\\S < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}\dfrac{2}{m} > 0\\\dfrac{{2\left( {m + 1} \right)}}{m} < 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > 0\\ - 1 < m < 0\end{array} \right.\,\,\,\left( {ktm} \right)\)

Vậy \(m < 0\) thì phương trình \(\left( 1 \right)\) có  nghiệm âm.