Đề kiểm tra giữa học kì 2 Vật lí 11 - Đề số 03 có lời giải chi tiết

Đề bài

A. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1: Một vòng dây dẫn tròn có diện tích \(0,4\,\,{m^2}\) đặt trong từ trường đều có cảm ứng từ \(B = 0,6\,\,T\), vecto cảm ứng từ vuông góc với mặt phẳng vòng dây. Nếu cảm ứng từ tăng đến \(1,4\,\,T\) trong thời gian \(0,25\,\,s\) thì độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là

A. \(1,28\,\,V\).                  B. \(12,8\,\,V\).

C. \(3,2\,\,V\).                    D. \(32\,\,V\).

Câu 2: Nếu một vòng dây dẫn quay trong từ trường đều quanh một trục vuông góc với từ trường, dòng điện cảm ứng

A. đổi chiều sau mỗi vòng quay.

B. không đổi chiều.

C. đổi chiều sau mỗi một phần tư vòng.

D. đổi chiều sau nửa vòng quay.

Câu 3: Một electron bay vào không gian có từ trường đều có cảm ứng từ \(B = 0,2\,\,T\) với vận tốc ban đầu \({v_0} = {2.10^5}\,\,m/s\) theo phương song song với véc tơ cảm ứng từ. Lực Lorenxơ tác dụng vào electron có độ lớn là

A. \(3,{2.10^{ - 14}}\,\,N\).

B. \(3,{2.10^{ - 15}}\,\,N\).

C. \(6,{4.10^{ - 14}}\,\,N\).

D. \(0\,\,N\).

Câu 4: Dòng điện \(I = 1\,\,\left( A \right)\) chạy trong dây dẫn thẳng dài. Cảm ứng từ tại điểm \(M\) cách dây dẫn \(10\,\,\left( {cm} \right)\) có độ lớn là:

A. \({2.10^{ - 8}}\,\,T\).

B. \({2.10^{ - 6}}\,\,T\).

C. \({4.10^{ - 7}}\,\,T\).

D. \({4.10^{ - 6}}\,\,T\).

Câu 5: Năng lượng từ trường của ống dây dẫn có hệ số tự cảm \(L\), mang dòng điện \(i\), được tính bằng công thức

A. \(W = \frac{{L{i^2}}}{2}\).

B. \(W = \frac{{Li}}{2}\).

C. \(W = L{i^2}\).

D. \(W = \frac{{{L^2}i}}{2}\).

Câu 6: Độ lớn của lực Lorenxơ được tính theo công thức

A. \(f = \left| q \right|vB\cos \alpha \).

B. \(f = qvB\tan \alpha \).

C. \(f = \left| q \right|vB\sin \alpha \).

D. \(f = \left| q \right|vB\).

Câu 7: Phương của lực Lo-ren-xơ

A. vuông góc với mặt phẳng hợp bởi vecto vận tốc của hạt và vecto cảm ứng từ.

B. trùng với phương của vecto cảm ứng từ.

C. trùng với mặt phẳng tạo bởi vecto vận tốc của hạt và vecto cảm ứng từ.

D. trùng với phương của vecto vận tốc của hạt mang điện.

Câu 8: Một hạt tích điện chuyển động trong từ trường đều, mặt phẳng quỹ đạo của hạt vuông góc với đường sức từ. Nếu hạt chuyển động với vận tốc \({v_1} = 1,{8.10^6}\,\,m/s\) thì lực Lorenxơ tác dụng lên hạt có giá trị \({2.10^{ - 6\,}}\,N\), nếu hạt chuyển động với vận tốc \({v_2} = {9.10^6}\,\,m/s\) thì lực Lorenxơ tác dụng lên hạt có giá trị là

A. \({5.10^{ - 5}}\,\,N\).

B. \(4,{5.10^{ - 5}}\,\,N\).

C. \(1,{0.10^{ - 5}}\,\,N\).

D. \(6,{8.10^{ - 5}}\,\,N\).

Câu 9: Hai dây dẫn thẳng dài, song song và cách nhau \(10\,\,cm\) trong chân không, dòng điện trong hai dây cùng chiều có cường độ \({I_1} = 2\,\,A\) và \({I_2} = 5\,\,A\). Lực từ tác dụng lên \(20\,\,cm\) chiều dài của mỗi dây là

A. lực đẩy có độ lớn \({4.10^{ - 7}}\,\,\left( N \right)\).

B. lực hút có độ lớn \({4.10^{ - 6}}\,\,\left( N \right)\).

C. lực hút có độ lớn \({4.10^{ - 7}}\,\,\left( N \right)\).

D. lực đẩy có độ lớn \({4.10^{ - 6}}\,\,\left( N \right)\).

Câu 10: Một khung dây hình vuông cạnh \(5\,\,cm\) đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4\,}}\,T\), từ thông qua hình vuông đó bằng \({10^{ - 6}}\,\,Wb\). Góc hợp bởi véctơ cảm ứng từ và véc tơ pháp tuyến của hình vuông đó là

A. \({30^0}\).                    B. \({0^0}\).

C. \({45^0}\).                    D. \({60^0}\).

Câu 11: Đáp án nào sau đây là sai. Hệ số tự cảm của ống dây

A. phụ thuộc vào cấu tạo và kích thước của ống dây.

B. được tính bằng công thức \(L = 4\pi {.10^{ - 7}}.NS/{\rm{l}}\).

C. càng lớn nếu số vòng dây trong ống dây càng nhiều.

D. có đơn vị là Henri (H).

Câu 12: Vật liệu nào sau đây không thể dùng làm nam châm?

A. Sắt và hợp chất của sắt.

B. Niken và hợp chất của niken.

C. Nhôm và hợp chất của nhôm.

D. Cô ban và hợp chất của cô ban.

Câu 13: Một đoạn dây dẫn\(\;CD\) chiều dài \({\rm{l}}\) mang dòng điện \(I\) chạy qua đặt trong từ trường sao cho \(\;CD\) song song với các đường sức từ. Độ lớn lực từ tác dụng lên dây \(\;CD\) là

A. \(F = BIS\sin \alpha \).

B. \(F = BI{\rm{l}}\).

C. \(F = 0\).

D. \(F = BI{\rm{l}}\cos \alpha \).

Câu 14: Phát biểu nào sau đây là không đúng? Người ta nhận ra từ trường tồn tại xung quanh dây dẫn mang dòng điện vì

A. có lực tác dụng lên một hạt mang điện chuyển động dọc theo nó.

B. có lực tác dụng lên một dòng điện khác đặt song song cạnh nó.

C. có lực tác dụng lên một hạt mang điện đứng yên đặt bên cạnh nó.

D. có lực tác dụng lên một kim nam châm đặt song song cạnh nó.

Câu 15: Một ống dây dài \(50\,\,cm\) tiết diện ngang là \(10\,\,c{m^2}\) gồm \(100\) vòng. Hệ số tự cảm của ống dây là

A. \(25\,\,\mu H\).              B. \(250\,\,\mu H\).

C. \(125\,\,\mu H\).            D. \(1250\,\,\mu H\).

Câu 16: Một đoạn dây dẫn dài \(10\,\,cm\) đặt trong từ trường đều và hợp với vectơ cảm ứng từ một góc \({30^0}\). Dòng điện chạy qua dây có cường độ \(0,75\,\,A\). Lực từ tác dụng lên đoạn dây đó là \(4,{5.10^{ - 2}}\,\,N\). Cảm ứng từ của từ trường đó có độ lớn là

A. \(1,0\,\,T\).                     B. \(1,2\,\,T\).

C. \(0,4\,\,T\).                     D. \(0,6\,\,T\).

Câu 17: Một dòng điện trong ống dây phụ thuộc vào thời gian theo biểu thức \(I = 0,4\left( {5 - t} \right);\,\,I\) tính bằng ampe, \(t\) tính bằng giây. Ống dây có hệ số tự cảm \(L = 0,005\,\,H\). Độ lớn suất điện động tự cảm trong ống dây là

A. \(0,001\,\,V\).                B. \(0,002\,\,V\).

C. \(0,003\,\,V\).                D. \(0.004\,\,V\).

Câu 18: Một khung dây dẫn phẳng có diện tích \(12\,\,c{m^2}\) đặt trong từ trường đều cảm ứng từ \(B = {5.10^{ - 2}}\,\,T\), mặt phẳng khung dây hợp với đường cảm ứng từ một góc \({30^0}\). Độ lớn từ thông qua khung là

A. \(\Phi  = {3.10^{ - 5}}\,\,Wb\).

B. \(\Phi  = {6.10^{ - 5}}\,\,Wb\).

C. \({4.10^{ - 5}}\,\,Wb\).

D. \(5,{1.10^{ - 5}}\,\,Wb\).

Câu 19: Một dây dẫn thẳng dài có dòng điện \(I\) chạy qua. Hai điểm \(M\) và \(N\) nằm trong cùng một mặt phẳng chứa dây dẫn, đối xứng với nhau qua dây. Gọi \(\overrightarrow {{B_M}} ;\,\,\overrightarrow {{B_N}} \) là cảm ứng từ tại \(M\)và \(N\). Kết luận nào sau đây không đúng?

A. \(M\)và \(N\)nằm trên cùng một đường sức từ.

B. \({B_M} = {B_N}\).

C. \(\overrightarrow {{B_M}} ;\,\,\overrightarrow {{B_N}} \) ngược chiều.     

D. \(\overrightarrow {{B_M}}  = \overrightarrow {{B_N}} \).

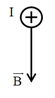
Câu 20: Một đoạn dây dẫn mang dòng điện đặt trong từ trường đều có các đường sức từ thẳng đứng hướng từ trên xuống như hình vẽ. Lực từ tác dụng lên đoạn dây có chiều

A. thẳng đứng hướng từ dưới lên.

B. nằm ngang hướng từ trái sang phải.

C. thẳng đứng hướng từ trên xuống dưới.

D. nằm ngang hướng từ phải sang trái.

Câu 21: Từ thông qua một mạch điện kín phụ thuộc vào

A. tiết diện của dây dẫn làm mạch điện.

B. khối lượng của dây dẫn làm mạch điện.

C. điện trở của dây dẫn làm mạch điện.

D. hình dạng, kích thước của mạch điện.

B. PHẦN TỰ LUẬN (3 điểm)

Câu 1 (1 điểm). Một khung dây dẫn hình vuông có cạnh \(10\,\,cm\) đặt trong từ trường đều có véc tơ cảm ứng từ vuông góc với mặt phẳng vòng dây. Nếu cho cảm ứng từ biến thiên với tốc độ \(5\,\,T/s\) thì độ lớn suất điện động cảm ứng xuất hiện trong khung dây?

Câu 2 (2 điểm). Hai dây dẫn thẳng dài vô hạn, song song cách nhau \(50\,\,cm\). Trong hai dây có hai dòng điện cường độ \({I_1} = 9\,\,A;\,\,{I_2} = 16\,\,A\) và ngược chiều chạy qua.

a. Tính độ lớn cảm ứng từ do hai dòng điện gây ra tại điểm \(M\) cách dòng \({I_1}\) một khoảng \(20\,\,cm\), cách dòng \({I_2}\) một khoảng \(30\,\,cm\).

b. Xác định véc tơ cảm ứng từ do hai dòng điện gây ra tại điểm \(N\) cách dòng \({I_1}\) một khoảng \(30\,\,cm\), cách dòng \({I_2}\) một khoảng \(40\,\,cm\).

Lời giải chi tiết

A. PHẦN TRẮC NGHIỆM

1. A	2. D	3. D	4. B	5. A	6. C	7. A
8. C	9. B	10. B	11. B	12. C	13. C	14. C
15. A	16. B	17. B	18. A	19. D	20. D	21. D

Câu 1:

Phương pháp:

Từ thông: \(\Phi  = NBS\cos \alpha \)

Suất điện động cảm ứng: \({e_c} =  - \frac{{\Delta \Phi }}{{\Delta t}}\)

Cách giải:

Độ lớn suất điện động cảm ứng xuất hiện trong vòng dây là:

\({e_c} = \left| { - \frac{{\Delta \Phi }}{{\Delta t}}} \right| = \frac{{S.\left| {\Delta B} \right|}}{{\Delta t}} = \frac{{0,4.\left| {1,4 - 0,6} \right|}}{{0,25}}\\ = 1,28\,\,\left( V \right)\)

Chọn A.

Câu 2:

Phương pháp:

Sử dụng lý thuyết cảm ứng điện từ

Cách giải:

Vòng dây dẫn quay trong từ trường đều quanh một trục vuông góc với từ trường, dòng điện cảm ứng đổi chiều sau nửa vòng quay

Chọn D.

Câu 3:

Phương pháp:

Lực Lo-ren-xơ: \({f_L} = \left| q \right|vB\sin \alpha \)

Cách giải:

Lực Lo-ren-xơ tác dụng lên electron là:

\({f_L} = \left| q \right|vB\sin \alpha \\ = \left| { - 1,{{6.10}^{ - 19}}} \right|{.2.10^5}.0,2.sin{0^0} = 0\,\,\left( N \right)\)

Chọn D.

Câu 4:

Phương pháp:

Cảm ứng từ do dòng điện thẳng gây ra: \(B = {2.10^{ - 7}}\frac{I}{r}\)

Cách giải:

Cảm ứng từ tại điểm \(M\) là:

\(B = {2.10^{ - 7}}\frac{I}{r} = {2.10^{ - 7}}.\frac{1}{{0,1}}\\ = {2.10^{ - 6}}\,\,\left( T \right)\)

Chọn B.

Câu 5:

Phương pháp:

Sử dụng lý thuyết tự cảm

Cách giải:

Năng lượng từ trường của ống dây là: \(W = \frac{{L{i^2}}}{2}\)

Chọn A.

Câu 6:

Phương pháp:

Sử dụng lý thuyết lực Lo-ren-xơ

Cách giải:

Công thức tính độ lớn lực Lo-ren-xơ: \(f = \left| q \right|vB\sin \alpha \)

Chọn C.

Câu 7:

Phương pháp:

Sử dụng lý thuyết lực Lo-ren-xơ

Cách giải:

Lực Lo-re-xơ có phương vuông góc với mặt phẳng hợp bởi vecto vận tốc của hạt và vecto cảm ứng từ

Chọn A.

Câu 8:

Phương pháp:

Lực Lo-ren-xơ: \({f_L} = \left| q \right|vB\sin \alpha \)

Cách giải:

Lực Lo-ren-xơ tác dụng lên điện tích là:

\({f_L} = \left| q \right|vB\sin \alpha  = \left| q \right|vB\sin {90^0} = \left| q \right|vB\\ \Rightarrow {f_L} \sim v\)

Ta có: \(\frac{{{f_2}}}{{{f_1}}} = \frac{{{v_2}}}{{{v_1}}} \\\Rightarrow {f_2} = {f_1}.\frac{{{v_2}}}{{{v_1}}} = {2.10^{ - 6}}.\frac{{{{9.10}^6}}}{{1,{{8.10}^6}}} \\= 1,{0.10^{ - 5}}\,\,\left( N \right)\)

Chọn C.

Câu 9:

Phương pháp:

Hai dòng điện cùng chiều, lực tương tác là lực hút

Hai dòng điện ngược chiều, lực tương tác là lực đẩy

Lực tương tác giữa hai dây dẫn thẳng song song có dòng điện chạy qua: \(F = {2.10^{ - 7}}.\frac{{{I_1}{I_2}}}{d}.{\rm{l}}\)

Cách giải:

Hai dòng điện cùng chiều, lực tương tác giữa hai dây dẫn là lực hút

Lực tương tác giữa hai dây dẫn là:

\(F = {2.10^{ - 7}}.\frac{{{I_1}{I_2}}}{d}.{\rm{l}} = {2.10^{ - 7}}.\frac{{2.5}}{{0,1}}.0,2\\ = {4.10^{ - 6}}\,\,\left( N \right)\)

Chọn B.

Câu 10:

Phương pháp:

Từ thông: \(\Phi  = BS\cos \alpha \) với \(\alpha  = \left( {\overrightarrow B ;\overrightarrow n } \right)\)

Cách giải:

Từ thông qua khung dây là:

\(\Phi  = BS\cos \alpha  \Rightarrow \cos \alpha  = \frac{\Phi }{{BS}}\\ = \frac{\Phi }{{B.{a^2}}} = \frac{{{{10}^{ - 6}}}}{{{{4.10}^{ - 4}}.0,{{05}^2}}} = 1\\ \Rightarrow \alpha  = {0^0}\)

Chọn B.

Câu 11:

Phương pháp:

Sử dụng lý thuyết hệ số tự cảm của ống dây

Cách giải:

Công thức tính hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}.{N^2}S/{\rm{l}} \to \) B sai

Chọn B.

Câu 12:

Phương pháp:

Sử dụng lý thuyết từ trường

Cách giải:

Vật liệu không thể dùng làm nam châm là nhôm và hợp chất của nhôm

Chọn C.

Câu 13:

Phương pháp:

Sử dụng lý thuyết lực từ

Cách giải:

Độ lớn lực từ tác dụng lên đoạn dây dẫn mang dòng điện đặt trong từ trường là:

\(F = BI{\rm{l}}\sin \alpha  = BI{\rm{l}}\sin {0^0} = 0\)

Chọn C.

Câu 14:

Phương pháp:

Sử dụng lý thuyết từ trường

Cách giải:

Từ trường không tác dụng lực lên điện tích đứng yên

Chọn C.

Câu 15:

Phương pháp:

Hệ số tự cảm của ống dây: \(L = 4\pi {.10^{ - 7}}.{N^2}S/{\rm{l}}\)

Cách giải:

Hệ số tự cảm của ống dây là:

\(L = 4\pi {.10^{ - 7}}.\frac{{{N^2}S}}{{\rm{l}}} \\= 4\pi {.10^{ - 7}}.\frac{{{{100}^2}.\left( {{{10.10}^{ - 4}}} \right)}}{{0,5}} \approx {25.10^{ - 6}}\,\,\left( H \right) \\= 25\,\,\left( {\mu H} \right)\)

Chọn A.

Câu 16:

Phương pháp:

Lực từ: \(F = IB{\rm{l}}\sin \alpha \)

Cách giải:

Lực từ tác dụng lên đoạn dây dẫn là:

\(F = IB{\rm{l}}\sin \alpha \\ \Rightarrow B = \frac{F}{{I{\rm{l}}\sin \alpha }} = \frac{{4,{{5.10}^{ - 2}}}}{{0,75.0,1.\sin {{30}^0}}} \\= 1,2\,\,\left( T \right)\)

Chọn B.

Câu 17:

Phương pháp:

Suất điện động tự cảm: \({e_c} =  - L\frac{{\Delta i}}{{\Delta t}}\)

Cách giải:

Cường độ dòng điện tại các thời điểm \({t_1};\,\,{t_2}\) là:

\(\begin{array}{l}\left\{ \begin{array}{l}{I_1} = 0,4.\left( {5 - {t_1}} \right)\\{I_2} = 0,4.\left( {5 - {t_2}} \right)\end{array} \right.\\ \Rightarrow \Delta i = {I_2} - {I_1} = 0,4.\left( {5 - {t_2}} \right)\\ = 0,4.\left( {5 - {t_1}} \right) = 0,4.\left( {{t_1} - {t_2}} \right) =  - 0,4.\Delta t\end{array}\)

Độ lớn suất điện động tự cảm trong ống dây là:

\({e_c} = \left| { - L\frac{{\Delta i}}{{\Delta t}}} \right| = L.\frac{{\left| {\Delta i} \right|}}{{\Delta t}} \\= 0,005.\frac{{\left| { - 0,4\Delta t} \right|}}{{\Delta t}} = 0,002\,\,\left( V \right)\)

Chọn B.

Câu 18:

Phương pháp:

Từ thông: \(\Phi  = BS\cos \alpha \) với \(\alpha  = \left( {\overrightarrow B ;\overrightarrow n } \right)\)

Cách giải:

Góc lệch giữa vecto cảm ứng từ và vecto pháp tuyến của mặt phẳng khung dây là:

\(\alpha  = {90^0} - {30^0} = {60^0}\)

Từ thông qua khung dây là:

\(\Phi  = BS\cos \alpha  = {5.10^{ - 2}}.\left( {{{12.10}^{ - 4}}} \right).\cos {60^0} \\= {3.10^{ - 5}}\,\,\left( {Wb} \right)\)

Chọn A.

Câu 19:

Phương pháp:

Đường sức từ do dòng điện thẳng gây ra là những đường tròn đồng tâm

Cảm ứng từ do dòn điện thẳng gây ra: \(B = {2.10^{ - 7}}\frac{I}{r}\)

Cách giải:

Hai điểm \(M,\,\,N\) đối xứng nhau qua dây dẫn \( \to {r_M} = {r_N}\)

\(M,N\) thuộc cùng một đường tròn \( \to M,N\) nằm trên cùng một đường sức từ → A đúng

\({B_M} = {B_N} \to \) B đúng

\(\overrightarrow {{B_M}}  =  - \overrightarrow {{B_N}}  \to \) C đúng, D sai

Chọn D.

Câu 20:

Phương pháp:

Áp dụng quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, chiều từ cổ tay đến các ngón tay trùng với chiều dòng điện, thì ngón cái choãi ra \({90^0}\) chỉ chiều của lực từ tác dụng lên dòng điện

Cách giải:

Áp dụng quy tắc bàn tay trái, lực từ tác dụng lên đoạn dây có chiều nằm ngang hướng từ phải sang trái

Chọn D.

Câu 21:

Phương pháp:

Từ thông qua mạch điện kín:

\(\Phi  = NBS\cos \alpha \) với \(\alpha  = \left( {\overrightarrow B ;\overrightarrow n } \right)\)

Cách giải:

Từ thông qua mạch điện kín phụ thuộc vào hình dạng, kích thước của mạch điện

Chọn D.

B. Phần tự luận

Câu 1:

Phương pháp:

Từ thông: \(\Phi  = BS\cos \alpha \)

Suất điện động cảm ứng: \({e_c} =  - \frac{{\Delta \Phi }}{{\Delta t}}\)

Cách giải:

Độ lớn suất điện động cảm ứng trong khung dây là:

\({e_c} = \left| { - \frac{{\Delta \Phi }}{{\Delta t}}} \right| = \frac{{S\left| {\Delta B} \right|}}{{\Delta t}} = {a^2}.\frac{{\left| {\Delta B} \right|}}{{\Delta t}}\\ = 0,{1^2}.5 = 0,05\,\,\left( V \right)\)

Câu 2:

Phương pháp:

Áp dụng quy tắc nắm tay phải xác định chiều của từ trường

Cảm ứng từ do dòng điện thẳng gây ra: \(I = {2.10^{ - 7}}\frac{I}{r}\)

Nguyên lí chồng chất từ trường: \(\overrightarrow B  = \overrightarrow {{B_1}}  + \overrightarrow {{B_2}}  + ...\)

Cách giải:

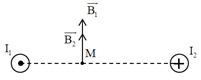
a. Điểm \(M\) nằm giữa hai dòng điện, áp dụng quy tắc nắm tay phải, ta có hình vẽ:

Từ hình vẽ ta thấy \(\overrightarrow {{B_1}}  \uparrow  \uparrow \overrightarrow {{B_2}}  \Rightarrow B = {B_1} + {B_2}\)

\(\begin{array}{l}B = {2.10^{ - 7}}.\frac{{{I_1}}}{{{r_1}}} + {2.10^{ - 7}}\frac{{{I_2}}}{{{r_2}}}\\ = {2.10^{ - 7}}.\left( {\frac{{{I_1}}}{{{r_1}}} + \frac{{{I_2}}}{{{r_2}}}} \right)\\ \Rightarrow B = {2.10^{ - 7}}.\left( {\frac{9}{{0,2}} + \frac{{16}}{{0,3}}} \right)\\ = 1,{97.10^{ - 5}} \approx {2.10^{ - 5}}\,\,\left( T \right)\end{array}\)

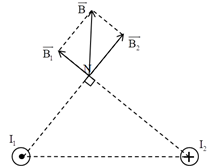
b. Điểm \(N\) cách dòng \({I_1}\) một khoảng \(30\,\,cm\), cách dòng \({I_2}\) một khoảng \(40\,\,cm\), áp dụng quy tắc nắm tay phải, ta có hình vẽ:

Từ hình vẽ ta thấy: \(\overrightarrow {{B_1}}  \bot \overrightarrow {{B_2}}  \Rightarrow B = \sqrt {{B_1}^2 + {B_2}^2} \)

\(\begin{array}{l} \Rightarrow B = \sqrt {{{\left( {{{2.10}^{ - 7}}.\frac{{{I_1}}}{{{r_1}}}} \right)}^2} + {{\left( {{{2.10}^{ - 7}}.\frac{{{I_2}}}{{{r_2}}}} \right)}^2}}\\  = {2.10^{ - 7}}.\sqrt {{{\left( {\frac{{{I_1}}}{{{r_1}}}} \right)}^2} + {{\left( {\frac{{{I_2}}}{{{r_2}}}} \right)}^2}} \\ \Rightarrow B = {2.10^{ - 7}}.\sqrt {{{\left( {\frac{9}{{0,3}}} \right)}^2} + {{\left( {\frac{{16}}{{0,4}}} \right)}^2}}  \\= {1.10^{ - 5}}\,\,\left( T \right)\end{array}\).