Đề kiểm tra giữa học kì 1 Vật lí 12 - Đề số 02 có lời giải chi tiết
Đề kiểm tra giữa kì 1 vật lí 12 - Đề số 02 được biên soạn theo hình thức trắc nghiệm có lời giải chi tiết giúp các em ôn tập hiệu quả chuẩn bị cho bài kiểm tra trên lớp
Đề bài
Câu 1: Một vật dao động tắt dần có các đại lượng nào sau đây giảm liên tục theo thời gian?
A. Biên độ và tốc độ
B. Li độ và tốc độ
C. Biên độ và gia tốc
D. Biên độ và cơ năng
Câu 2: Tại mặt thoáng của một chất lỏng có hai nguồn \({S_1}\) và \({S_2}\) dao động theo phương thẳng đứng với cùng phương trình \(u = acos40\pi t\left( {cm} \right)\) (a không đổi, t tính bằng s). Tốc độ truyền sóng trên mặt chất lỏng bằng \(80cm/s\). Khoảng cách ngắn nhất giữa hai phần tử chất lỏng trên đoạn thẳng \({S_1}{S_2}\) dao động với biên độ cực đại là
A. \(4cm\) B. \(6cm\)
C. \(2cm\) D. \(1cm\)
Câu 3: Một sóng cơ có chu kì \(2s\) truyền với tốc độ \(1m/s\). Khoảng cách giữa hai điểm gần nhau nhất trên một phương truyền mà tại đó các phần tử môi trường dao động cùng pha nhau là
A. \(0,5m\) B. \(2,5m\)
C. \(2,0m\) D. \(1,0m\)
Câu 4: Sóng dừng trên dây AB có chiều dài \(32cm\) với hai đầu \(A,B\) cố định. Tần số sóng của dây là \(50Hz\), tốc độ truyền sóng trên dây là \(4m/s\). Trên dây (kể cả A, B) có:
A. 5 nút, 4 bụng
B. 4 nút, 4 bụng
C. 8 nút, 8 bụng
D. 9 nút, 8 bụng
Câu 5: Cơ năng của một vật dao động điều hòa
A. bằng động năng của vật khi vật tới vị trí cân bằng.
B. tăng gấp đôi khi biên độ dao động của vật tăng gấp đôi.
C. biến thiên tuần hoàn theo thời gian với chu kì bằng một nửa chu kì dao động của vật.
D. biến thiên tuần hoàn theo thời gian với chu kì bằng chu kì dao động của vật.
Câu 6: Khi nói về một vật đang dao động điều hòa, phát biểu nào sau đây là đúng?
A. Vector gia tốc của vật đổi chiều khi vật có li độ cực đại.
B. Vector vận tốc và vector gia tốc của vật cùng chiều nhau khi vật chuyển động về phía vị trí cân bằng.
C. Vector gia tốc của vật luôn hướng ra xa vị trí cân bằng.
D. Vector vận tốc và vector gia tốc của vật cùng chiều nhau khi vật chuyển động ra xa vị trí cân bằng.
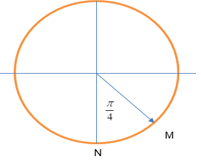
Câu 7: Một chất điểm dao động điều hòa theo trục Ox với phương trình \(x = 6cos\left( {5\pi t - \frac{\pi }{3}} \right)\left( {cm,s} \right)\) . Tính từ thời điểm \(t = 0\), chất điểm đi qua vị trí có li độ \( - 3\sqrt 3 cm\) theo chiều dương lần thứ \(2018\) tại thời điểm
A. \(807,1s\) B. \(806,9s\)
C. \(403,3s\) D. \(403,4s\)
Câu 8: Trong thí nghiệm giao thoa trên mặt nước, hai nguồn kết hợp cùng pha, dao động với tần số \(80Hz\), tốc độ truyền sóng \(0,8m/s\). Tính từ đường trung trực của 2 nguồn, điểm M cách hai nguồn lần lượt \(20,25cm\) và \(26,75cm\) nằm trên đường
A. cực tiểu thứ 6
B. cực tiểu thứ 7
C. cực đại bậc 6
D. cực đại bậc 7
Câu 9: Đồ thị quan hệ giữa vận tốc và li độ của một vật dao động điều hòa là đường
A. hình sin B. parabol
C. elip D. thẳng
Câu 10: Tại một vị trí trong môi trường truyền âm, khi cường độ âm tăng gấp 10 lần thì mức cường độ âm
A. giảm đi 10B
B. tăng thêm 10B
C. tăng thêm 10dB
D. giảm đi 10dB
Câu 11: Một vật nhỏ dao động điều hòa thực hiện \(2018\) dao động toàn phần trong \(1009s\). Tần số dao động là
A. \(4\pi Hz\) B. \(0,5Hz\)
C. \(1Hz\) D. \(2Hz\)
Câu 12: Đơn vị đo mức cường độ âm là
A. Oát trên mét (W/m)
B. đề-xi-ben (dB)
C. Niuton trên mét vuông (N/m2)
D. Oát trên mét vuông (W/m2)
Câu 13: Nốt La phát ra từ hai nhạc cụ khác nhau thì chắc chắn khác nhau về
A. âm sắc B. độ cao
C. độ to D. tần số
Câu 14: Một vật nhỏ dao động điều hòa trên trục Ox với phương trình \(x = 4cos\left( {5\pi t + \varphi } \right)cm\). Tại thời điểm pha của dao động là \(\frac{\pi }{3}\) rad thì vật có:
A. li độ \(2cm\) và theo chiều dương trục Ox.
B. li độ \(2cm\) và theo chiều âm trục Ox.
C. li độ \( - 2cm\) và theo chiều âm trục Ox.
D. li độ \( - 2cm\) và theo chiều dương trục Ox.
Câu 15: Con lắc lò xo dao động điều hòa. Khi giảm độ cứng của lò xo đi 3 lần và tăng khối lượng vật 3 lần thì chu kì dao động của con lắc
A. tăng lên 9 lần.
B. không đổi
C. tăng lên 3 lần
D. giảm đi 3 lần
Câu 16: Chu kì dao động là
A. Khoảng thời gian ngắn nhất để vật trở về lại trạng thái ban đầu.
B. Khoảng thời gian để vật đi từ bên này sang bên kia của quỹ đạo chuyển động.
C. Khoảng thời gian ngắn nhất để vật trở lại vị trí ban đầu.
D. Số dao động toàn phần vật thực hiện được trong 1s.
Câu 17: Để khảo sát giao thoa sóng cơ, người ta bố trí trên mặt nước nằm ngang hai nguồn kết hợp \({S_1}\) và \({S_2}\). Hai nguồn này dao động điều hòa theo phương thẳng đứng, cùng pha. Xem biên độ sóng không thay đổi trong quá trình truyền sóng. Các điểm thuộc mặt nước và nằm trên đường trung trực của đoạn \({S_1}{S_2}\) sẽ:
A. dao động với biên độ bằng nửa biên độ cực đại.
B. dao động với biên độ cực tiểu
C. dao động với biên độ cực đại
D. không dao động
Câu 18: Hai dao động điều hòa thành phần cùng phương, cùng tần số, ngược pha có biên độ là \({A_1}\) và \({A_2}\) với \({A_2} = 3{A_1}\) thì dao động tổng hợp có biên độ là
A. \({A_1}\) B. \(2{A_1}\)
C. \(3{A_1}\) D. \(4{A_1}\)
Câu 19: Một người quan sát trên mặt nước biển thấy một cái phao nhô lên 5 lần trong 20s và khoảng cách giữa hai đỉnh sóng liên tiếp là 2m. Tốc độ truyền sóng biển là
A. \(40cm/s\) B. \(50cm/s\)
C. \(60cm/s\) D. \(80cm/s\)
Câu 20: Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động
A. cùng tần số, cùng phương.
B. cùng biên độ và có hiệu số pha không đổi theo thời gian.
C. có cùng pha ban đầu và cùng biên độ.
D. cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian.
Câu 21: Tại một vị trí trên mặt đất, con lắc đơn có chiều dài \({l_1}\) dao động với chu kì \({T_1}\), con lắc đơn có chiều dài \({l_2}\) thì dao động với chu kì \({T_2}\). Cũng tại vị trí đó, con lắc đơn có chiều dài \({l_1} + {l_2}\) sẽ dao động với chu kì T thỏa mãn
A. \(T = {T_1} + {T_2}\)
B. \({T^2} = T_1^2 + T_2^2\)
C. \({T^2} = T_2^2 - T_1^2\)
D. \(\sqrt T = \sqrt {{T_1}} + \sqrt {{T_2}} \)
Câu 22: Một vật nhỏ khối lượng \(100g\) dao động điều hòa với biên độ \(4cm\) và tần số \(5Hz\). Lấy \({\pi ^2} = 10\). Lực kéo về tác dụng lên vật có độ lớn cực đại bằng
A. \(5N\) B. \(400N\)
C.\(4N\) D. \(2N\)
Câu 23: Để có sóng dừng xảy ra trên một sợi dây đàn hồi với một đầu dây cố định, một đầu tự do thì
A. chiều dài dây bằng số nguyên nửa bước sóng.
B. chiều dài dây bằng số lẻ một phần tư bước sóng.
C. chiều dài dây bằng số nguyên một phần tư bước sóng.
D. chiều dài dây bằng số lẻ nửa bước sóng.
Câu 24: Hai điểm M, N cùng nằm trên một hướng truyền sóng và cách nhau một phần tám bước sóng. Sóng truyền từ M đến N. Biên độ sóng không đổi trong quá trình truyền sóng, chu kì sóng là T. Tại một thời điểm t, vận tốc của phần tử tại N có giá trị cực đại. Khoảng thời gian ngắn nhất sau đó M tới biên dương là
A. \(\frac{{3T}}{4}\) B. \(\frac{T}{8}\)
C. \(\frac{T}{6}\) D. \(\frac{{3T}}{8}\)
Câu 25: Bước sóng là khoảng cách giữa hai điểm
A. trên cùng một phương truyền sóng mà dao động tại hai điểm đó ngược pha.
B. gần nhau nhất trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
C. gần nhau nhất mà dao động tại hai điểm đó cùng pha.
D. trên cùng một phương truyền sóng mà dao động tại hai điểm đó cùng pha.
Câu 26: Một vật có khối lượng \(50g\), dao động điều hòa với biên độ \(4cm\) và tần số góc \(3rad/s\). Động năng cực đại của vật là
A. \(3,6J\) B. \(7,2J\)
C. \(3,{6.10^{ - 4}}J\) D. \(7,{2.10^{ - 4}}J\)
Câu 27: Khảo sát hiện tượng sóng dừng trên dây đàn hồi AB. Đầu A nối với nguồn dao động, đầu B tự do thì sóng tới và sóng phản xạ tại B.
A. cùng pha.
B. lệch pha góc \(\frac{\pi }{4}\)
C. vuông pha
D. ngược pha
Câu 28: Phát biểu nào sau đây là sai khi nói về dao động của con lắc đơn (bỏ qua lực cản của môi trường)
A. Khi vật nặng ở vị trí biên, cơ năng của con lắc bằng thế năng của nó.
B. Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần.
C. Khi vật nặng đi qua vị trí cân bằng, thì trọng lực tác dụng lên nó cân bằng với lực căng của dây.
D. Với dao động nhỏ thì dao động của con lắc là dao động điều hòa.
Câu 29: Cho một vật dao động điều hòa. Khi li độ là \(x = {x_0}\) thì động năng của vật gấp n lần thế năng của lò xo \(\left( {n > 1} \right)\). Khi li độ là \(x = 0,5{x_0}\) thì
A. động năng của vật gấp \(2n\) lần thế năng của lò xo
B. thế năng của lò xo gấp \(4n + 3\) lần động năng của vật
C. động năng của vật gấp \(4n + 3\)lần thế năng của lò xo
D. thế năng của lò xo gấp \(2n\) lần động năng của vật
Câu 30: Một hòn bi nhỏ khối lượng m treo ở đầu một sợi dây và dao động nhỏ tại nơi có gia tốc trọng trường g. Chu kì dao động thay đổi bao nhiêu lần nếu hòn bi được tích một điện tích \(q > 0\) và đặt trong một điện trường đều có vector cường độ \(\overrightarrow E \) thẳng đứng hướng xuống dưới sao cho \(qE = 3mg\).
A. tăng 2 lần. B. giảm 3 lần
C. tăng 3 lần D. giảm 2 lần
Câu 31: Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha đặt tại hai điểm A và B cách nhau \(16cm\). Sóng truyền trên mặt nước với bước sóng \(3cm\). Trên đoạn \(AB\), số điểm mà tại đó phần tử nước dao động với biên độ cực đại là:
A. 9 B. 10
C. 11 D. 12
Câu 32: Tại nơi có gia tốc trọng trường là \(9,8m/{s^2}\), một con lắc đơn dao động điều hòa với biên độ góc \({6^0}\). Biết khối lượng vật nhỏ của con lắc là \(90g\) và chiều dài đây treo là \(1m\). Chọn mốc thế năng tại vị trí cân bằng, cơ năng của con lắc xấp xỉ bằng
A. \(6,{8.10^{ - 3}}J\) B. \(3,{8.10^{ - 3}}J\)
C. \(5,{8.10^{ - 3}}J\) D. \(4,{8.10^{ - 3}}J\)
Câu 33: Sóng dừng xảy ra trên một sợi dây đàn hồi dài \({l_0}\) hai đầu cố định. Sóng truyền trên dây với vận tốc truyền sóng \(v\). Để có sóng dừng thì tần số dao động của dây nhỏ nhất được tính:
A. \({f_{\min }} = \frac{v}{{4{l_0}}}\)
B. \({f_{\min }} = \frac{{2{l_0}}}{v}\)
C. \({f_{\min }} = \frac{v}{{2{l_0}}}\)
D. \({f_{\min }} = \frac{{4{l_0}}}{v}\)
Câu 34: Một xe ô tô chạy trên đường, cứ \(8m\) lại có một cái mô nhỏ. Chu kì dao động tự do của khung xe trên các lò xo là \(1,5s\). Xe chạy với tốc độ nào thì bị rung mạnh nhất?
A. \(19,2km/h\) B. \(18,9km/h\)
C. \(16,3km/h\) D. \(12,7km/h\)
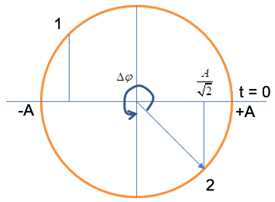
Câu 35: Một vật dao động điều hòa trên trục Ox. Khoảng thời gian ngắn nhất từ khi gia tốc của vật đạt giá trị cực đại tới khi vận tốc của vật đạt giá trị cực đại là \(0,5s\). Thời điểm ban đầu, lực kéo về có giá trị cực đại. Thời điểm vật có li độ x và vận tốc thỏa mãn \(v = \omega x\) lần thứ \(2018\) là
A. \(2016,75s\) B. \(1006,25s\)
C. \(2017,75s\) D. \(1008,75s\)
Câu 36: Một con lắc lò xo gồm vật nhỏ khối lượng \(40g\) và lò xo có độ cứng \(20N/m\). Vật nhỏ được đặt trên giá đỡ cố định nằm ngang dọc theo trục lò xo. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là \(0,2\). Lấy \(g = 10m/{s^2}\). Ban đầu giữ vật ở vị trí lò xo bị dãn \(6cm\) rồi buông nhẹ. Tốc độ lớn nhất vật nhỏ đạt được trong quá trình chuyển động của vật là
A. \(1,54m/s\) B. \(1,34m/s\)
C. \(1,25m/s\) D. \(1,75m/s\)
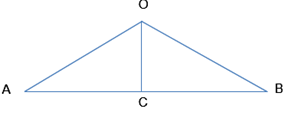
Câu 37: Tại O có một nguồn âm phát âm thanh đẳng hướng với công suất không đổi. Một máy thu di chuyển theo một đường thẳng từ A đến B với \(AB = 16\sqrt 2 cm\), thấy tại A có cường độ âm là I sau đó cường độ âm tăng tới 9I tại C rồi lại giảm dần về I tại B. Khoảng cách \(OC\) là
A. \(4cm\) B. \(8cm\)
C. \(4\sqrt 2 cm\) D. \(6\sqrt 2 cm\)
Câu 38: Một chát điểm khối lượng \(200g\) dao động điều hòa trên trục Ox với cơ năng \(0,1J\). Trong khoảng thời gian \(\Delta t = \frac{\pi }{{20}}s\), động năng của vật tăng từ giá trị \(25mJ\) đến giá trị cực đại rồi giảm về \(75mJ\). Vật dao động với biên độ
A. \(1m\) B. \(1,0cm\)
C. \(12cm\) D. \(10cm\)
Câu 39: Trên sợi dây dài \(24cm\), hai đầu cố định, đang có sóng dừng với 2 bụng sóng. Khi dây duỗi thẳng, M và N là hai điểm trên dây chia sợi dây thành 3 đoạn bằng nhau. Tỉ số khoảng cách lớn nhất và nhỏ nhất giữa hai điểm M và N bằng \(1,25\). Biên độ dao động tại bụng sóng là
A. \(3\sqrt 3 cm\) B. \(4cm\)
C. \(5cm\) D. \(2\sqrt 3 cm\)
Câu 40: Tại hai điểm A và B trên mặt nước cách nhau \(16cm\) có 2 nguồn kết hợp dao động điều hòa cùng tần số, cùng pha, điểm M nằm trên mặt nước và nằm trên đường trung trực của AB cách trung điểm I của AB một khoảng nhỏ nhất bằng \(4\sqrt 5 cm\) luôn dao động cùng pha với I. Điểm N nằm trên mặt nước và nằm trên đường thẳng vuông góc với AB tại A, cách A một khoảng nhỏ nhất bằng bao nhiêu để N không dao động?
A. \(2,14cm\) B. \(9,22cm\)
C. \(8,75cm\) D. \(8,57cm\)
Lời giải chi tiết
|
1.D |
2.C |
3.C |
4.D |
5.A |
6.B |
7.A |
8.B |
9.C |
10.C |
|
11.D |
12.B |
13.A |
14.B |
15.C |
16.A |
17.C |
18.B |
19.A |
20.D |
|
21.B |
22.C |
23.B |
24.B |
25.B |
26.C |
27.A |
28.C |
29.C |
30.D |
|
21.C |
32.D |
33.C |
34.A |
35.C |
36.C |
37.A |
38.D |
39.D |
40.A |
Câu 1:
Phương pháp giải:
Sử dụng lí thuyết về các loại dao động
Lời Giải:
Dao động tắt dần là dao động có biên độ giảm dần theo thời gian.
Lại có: cơ năng \({\rm{W}} = \frac{1}{2}k{A^2}\) \( \Rightarrow \) Cơ năng cũng giảm theo thời gian
Chọn D.
Câu 2:
Phương pháp giải:
+ Đọc phương trình sóng
+ Sử dụng biểu thức tính tần số: \(f = \frac{\omega }{{2\pi }}\)
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \frac{v}{f}\)
Lời Giải:
Ta có:
+ \(\omega = 40\pi \left( {rad/s} \right)\) \( \Rightarrow f = \frac{\omega }{{2\pi }} = \frac{{40\pi }}{{2\pi }} = 20Hz\)
+ Bước sóng: \(\lambda = \frac{v}{f} = \frac{{80}}{{20}} = 4cm\)
Khoảng cách ngắn nhất giữa 2 điểm dao động với biên độ cực đại là \(\frac{\lambda }{2} = \frac{4}{2} = 2cm\)
Chọn C.
Câu 3:
Phương pháp giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = v.T\)
+ Vận dụng định nghĩa về bước sóng
Lời Giải:
Ta có, bước sóng \(\lambda = vT = 1.2 = 2m\)
Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha nhau chính là một bước sóng \(\lambda = 2m\)
Chọn C.
Câu 4:
Phương pháp giải:
Sử dụng điều kiện xảy ra sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}\)
Với k = số bụng = số nút - 1
Lời Giải:
+ Bước sóng: \(\lambda = \frac{v}{f} = \frac{4}{{50}} = 0,08m = 8cm\)
Ta có, AB hai đầu cố định, khi đó: \(l = k\frac{\lambda }{2} \Leftrightarrow 32 = k\frac{8}{2} \Rightarrow k = 8\)
\( \Rightarrow \) Trên dây có 8 bụng sóng, 9 nút sóng (kể cả A và B)
Chọn D.
Câu 5:
Phương pháp giải:
Vận dụng lí thuyết và biểu thức tính cơ năng: \({\rm{W}} = \frac{1}{2}k{A^2}\)
Lời Giải:
A – đúng
B – sai vì cơ năng tăng gấp 4 khi biên độ tăng gấp đôi
C, D – sai vì cơ năng không đổi theo thời gian
Chọn A.
Câu 6:
Phương pháp giải:
Sử dụng lí thuyết về dao động điều hòa
Lời Giải:
A – sai vì vector gia tốc đổi chiều tại vị trí cân bằng
B – đúng
C – sai vì vector gia tốc luôn hướng về vị trí cân bằng
D - sai
Chọn B.
Câu 7:
Phương pháp giải:
+ Đọc phương trình dao động
+ Xác định số lần vật qua li độ x trong 1 chu kì
+ Sử dụng trục thời gian suy ra từ vòng tròn lượng giác
Lời Giải:
Ta có: \(x = 6cos\left( {5\pi t - \frac{\pi }{3}} \right)cm\)
Tại \(t = 0\): \(\left\{ \begin{array}{l}{x_0} = 6cos\left( { - \frac{\pi }{3}} \right) = 3cm\\{v_0} = - A\omega \sin \left( { - \frac{\pi }{3}} \right) > 0\end{array} \right.\)
Trong 1 chu kì, chất điểm qua vị trí \(x = - 3\sqrt 3 cm\) theo chiều dương 1 lần
\( \Rightarrow \) Thời điểm chất điểm qua vị trí \(x = - 3\sqrt 3 cm\) theo chiều dương lần thứ 2018 là: \({t_{2018}} = {t_{2017}} + {t_1}\)
Ta có: \({t_{2017}} = 2017T\)
\({t_1}\) là thời điểm vật qua vị trí \(x = - 3\sqrt 3 cm\) theo chiều dương lần 1 từ thời điểm ban đầu
(Tương ứng là thời điểm vật đi từ \(\frac{A}{2} \to A \to - A \to - \frac{{A\sqrt 3 }}{2}\) )
\( \Rightarrow {t_1} = \frac{T}{6} + 2\frac{T}{4} + \frac{T}{{12}} = \frac{{3T}}{4}\) \( \Rightarrow {t_{2018}} = {t_{2017}} + {t_1} = 2017T + \frac{{3T}}{4}\)
Lại có \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{5\pi }} = \frac{2}{5}\) \( \Rightarrow {t_{2018}} = 807,1s\)
Chọn A.
Câu 8:
Phương pháp giải:
+ Sử dụng biểu thức tính bước sóng: \(\lambda = \frac{v}{f}\)
+ Sử dụng điều kiện cực đại cực tiểu của 2 nguồn cùng pha
- Cùng pha: \({d_2} - {d_1} = k\lambda \)
- Cực tiểu: \({d_2} - {d_1} = \left( {k + \frac{1}{2}} \right)\lambda \)
Lời Giải:
+ Bước sóng: \(\lambda = \frac{v}{f} = \frac{{0,8}}{{80}} = 0,01m = 1cm\)
+ Tại điểm M: \({d_2} - {d_1} = 26,75 - 20,25\\ = \frac{{13}}{2}cm = \left( {6 + \frac{1}{2}} \right)\lambda \)
Do 2 nguồn cùng pha \( \Rightarrow \) M là cực tiểu thứ 7
Chọn B.
Câu 9:
Phương pháp giải:
Vận dụng lí thuyết về dao động điều hòa
Lời Giải:
Ta có: \(\frac{{{x^2}}}{{{A^2}}} + \frac{{{v^2}}}{{{A^2}{\omega ^2}}} = 1\)
\( \Rightarrow \) Đồ thị quan hệ giữa vận tốc và li độ của một vật dao động điều hòa là elip
Chọn C.
Câu 10:
Phương pháp giải:
Sử dụng biểu thức tính mức cường độ âm: \(L = \log \frac{I}{{{I_0}}}\)
Lời Giải:
Ban đầu: \({I_1} = I\) thì \({L_1} = \log \frac{{{I_1}}}{{{I_0}}}\)
Khi tăng cường độ âm: \({I_2} = 10{I_1} = 10I\) thì \({L_2} = \log \frac{{{I_2}}}{{{I_0}}} = \log \frac{{10{I_1}}}{{{I_0}}} = 1 + \log \frac{{{I_1}}}{{{I_0}}}\left( B \right)\)
\( \Rightarrow \) Mức cường độ âm tăng thêm 1B = 10dB
Chọn C.
Câu 11:
Phương pháp giải:
Sử dụng biểu thức xác định tần số: \(f = \frac{N}{{\Delta t}}\)
Lời Giải:
Tần số dao động của vật: \(f = \frac{N}{{\Delta t}} = \frac{{2018}}{{1009}} = 2Hz\)
Chọn C.
Câu 12:
Phương pháp giải:
Sử dụng lí thuyết về mức cường độ âm
Lời Giải:
Đơn vị của mức cường độ âm là Ben (B) hoặc đềxiben (dB)
Chọn B.
Câu 13:
Phương pháp giải:
Sử dụng lí thuyết về đặc trưng sinh lí – vật lí của âm
Lời Giải:
Nốt La phát ra từ hai nhạc cụ khác nhau thì chắc chắn khắc nhau về âm sắc.
Chọn A.
Câu 14:
Phương pháp giải:
+ Đọc phương trình dao động điều hòa
+ Sử dụng lí thuyết về dao động cơ
Lời Giải:
Tại thời điểm pha của dao động là \(\frac{\pi }{3}rad\) thì:
+ Li độ: \(x = 4cos\frac{\pi }{3} = 2cm\)
+ Vận tốc: \(v = - 4.5\pi \sin \frac{\pi }{3} < 0\)
\( \Rightarrow \) Khi đó vật có li độ \(2cm\) và đang chuyển động theo chiều âm
Chọn B.
Câu 15:
Phương pháp giải:
Vận dụng biểu thức tính chu kì dao động của con lắc lò xo: \(T = 2\pi \sqrt {\frac{m}{k}} \)
Lời Giải:
Ta có: \(T = 2\pi \sqrt {\frac{m}{k}} \)
\( \Rightarrow \) Khi k giảm 3 lần và m tăng 3 lần thì chu kì dao động tăng lên 3 lần
Chọn C.
Câu 16:
Phương pháp giải:
Sử dụng định nghĩa về chu kì
Lời Giải:
Chu kì là khoảng thời gian ngắn nhất để vật trở lại trạng thái ban đầu.
Chọn A.
Câu 17:
Phương pháp giải:
Vận dụng lí thuyết về giao thoa sóng cơ học.
Lời Giải:
Do 2 nguồn cùng pha
\( \Rightarrow \) Các điểm trên trung trực của \({S_1}{S_2}\) sẽ dao động với biên độ cực đại.
Chọn C.
Câu 18:
Phương pháp giải:
Vận dụng về tổng hợp dao động điều hòa của 2 nguồn ngược pha
Lời Giải:
Ta có, 2 nguồn dao động ngược pha
\( \Rightarrow \) Biên độ dao động tổng hợp: \(A = {A_2} - {A_1} = 3{A_1} - {A_1} = 2{A_1}\)
Chọn B.
Câu 19:
Phương pháp giải:
Vận dụng biểu thức: \(\lambda = vT\)
Lời Giải:
+ Chu kì dao động: \(T = \frac{{20}}{4} = 5s\)
+ Khoảng cách giữa 2 đỉnh sóng chính = bước sóng: \(\lambda = 2m\)
\( \Rightarrow \) Tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \frac{2}{5} = 0,4m/s = 40cm/s\)
Chọn A.
Câu 20:
Phương pháp giải:
Sử dụng điều kiện giao thoa sóng
Lời Giải:
Điều kiện giao thoa sóng là 2 sóng phải là 2 sóng kết hợp tức là: có cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian.
Chọn D.
Câu 21:
Phương pháp giải:
Vận dụng biểu thức tính chu kì: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Lời Giải:
Ta có, chu kì dao động \(T = 2\pi \sqrt {\frac{l}{g}} \)\( \Rightarrow {T^2} \sim l\)
Khi con lắc có chiều dài \({l_1} + {l_2}\) sẽ dao động với chu kì: \({T^2} = T_1^2 + T_2^2\)
Chọn B.
Câu 22:
Phương pháp giải:
Lực kéo về cực đại: \({F_{max}} = kA\)
Lời Giải:
Lực kéo về cực đại: \({F_{max}} = kA = m{\omega ^2}A \\= 0,1.{\left( {2\pi .5} \right)^2}0,04 = 4N\)
Chọn C.
Câu 23:
Phương pháp giải:
Vận dụng biểu thức sóng dừng trên dây 1 đầu cố định 1 đầu tự do: \(l = \left( {2k + 1} \right)\frac{\lambda }{4}\)
Lời Giải:
Sóng dừng trên dây 1 đầu cố định 1 đầu tự do: \(l = \left( {2k + 1} \right)\frac{\lambda }{4}\)
Chọn B.
Câu 24:
Phương pháp giải:
+ Sử dụng biểu thức xác định độ lệch pha giữa 2 điểm trên phương truyền sóng: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
+ Sử dụng vòng tròn lượng giác
Lời Giải:
+ Độ lệch pha giữa M và N trên phương truyền sóng: \(\Delta \varphi = \frac{{2\pi d}}{\lambda } = \frac{{2\pi \frac{\lambda }{8}}}{\lambda } = \frac{\pi }{4}\)
+ Tại thời điểm t: vận tốc tại N có giá trị cực đại \( \Rightarrow N\) đang ở VTCB \( \Rightarrow M\) đang ở vị trí \(\frac{{A\sqrt 2 }}{2}\) (do sóng truyền từ M đến N nên M nhanh pha hơn N một góc \(\frac{\pi }{4}\) )
Từ vòng tròn lượng giác \( \Rightarrow \) Thời gian ngắn nhất sau đó M tới biên dương là \(\frac{T}{8}\)
Chọn B.
Câu 25:
Phương pháp giải:
Sử dụng định nghĩa về bước sóng.
Lời Giải:
Bước sóng là khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha với nhau.
Chọn B.
Câu 26:
Phương pháp giải:
+ Sử dụng biểu thức tính vận tốc cực đại: \({v_{max}} = A\omega \)
+ Sử dụng biểu thức tính động năng cực đại: \({{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2\)
Lời Giải:
+ Vận tốc cực đại: \({v_{max}} = A\omega \)
+ Động năng cực đại: \({{\rm{W}}_{dmax}} = \frac{1}{2}mv_{max}^2 = \frac{1}{2}0,05.{\left( {3.0,04} \right)^2}\\ = 3,{6.10^{ - 4}}J\)
Chọn C.
Câu 27:
Phương pháp giải:
Sử dụng lí thuyết về sóng dừng trên dây
Lời Giải:
Khi khảo sát hiện tượng sóng dừng trên dây, đầu A nối với nguồn, đầu B tự do thì sóng tới và sóng phản xạ tại B cùng pha với nhau.
Chọn A.
Câu 28:
Phương pháp giải:
Vận dụng lí thuyết về dao động của con lắc đơn
Lời Giải:
A, B, D – đúng
C – sai
Chọn C.
Câu 29:
Phương pháp giải:
+ Vận dụng biểu thức tính thế năng: \({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)
+ Sử dụng biểu thức tính cơ năng: \({\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
Lời Giải:
Ta có:
+ Khi \(x = {x_0}\) thì thế năng \({{\rm{W}}_{{t_1}}} = \frac{1}{2}kx_0^2 = \frac{1}{n}{{\rm{W}}_{{d_1}}}\)
Cơ năng: \({\rm{W}} = {{\rm{W}}_{{t_1}}} + {{\rm{W}}_{{d_1}}} = \left( {n + 1} \right){{\rm{W}}_{{t_1}}}\)
+ Khi \(x = 0,5{x_0}\) thì thế năng \({{\rm{W}}_{{t_2}}} = \frac{1}{2}k{x^2} = \frac{1}{4}\frac{1}{2}kx_0^2 = \frac{1}{4}{{\rm{W}}_{{t_1}}}\)
Khi đó động năng: \({{\rm{W}}_{{d_2}}} = {\rm{W}} - {{\rm{W}}_{{t_2}}} \\= \left( {n + 1} \right){{\rm{W}}_{{t_1}}} - \frac{1}{4}{{\rm{W}}_1} = \left( {n + \frac{3}{4}} \right){{\rm{W}}_{{t_1}}}\)
\(\begin{array}{l} \Rightarrow \frac{{{{\rm{W}}_{{t_2}}}}}{{{{\rm{W}}_{{d_2}}}}} = \frac{{\frac{1}{4}}}{{n + \frac{3}{4}}} = \frac{1}{{4n + 3}}\\ \Rightarrow {W_{{d_2}}} = \left( {4n + 3} \right){{\rm{W}}_{{t_2}}}\end{array}\)
Chọn C.
Câu 30:
Phương pháp giải:
+ Sử dụng biểu thức tính lực điện: \({F_d} = qE\)
+ Vận dụng biểu thức tính chu kì dao động của con lắc đơn: \(T = 2\pi \sqrt {\frac{l}{g}} \)
Lời Giải:
+ Khi chưa đặt con lắc vào điện trường, chu kì dao động của con lắc: \({T_0} = 2\pi \sqrt {\frac{l}{g}} \)
+ Ta có con lắc đơn chịu tác dụng của lực điện có phương thẳng đứng, chiều hướng xuống
\({F_d} = qE\)
Khi đó, gia tốc của con lắc: \(g' = g + a\) với \(a = \frac{{qE}}{m}\)
\( \Rightarrow g' = g + \frac{{qE}}{m} = g + \frac{{3mg}}{m} = 4g\)
Chu kì dao động của con lắc khi này: \(T = 2\pi \sqrt {\frac{l}{{g'}}} = 2\pi \sqrt {\frac{l}{{4g}}} = \frac{{{T_0}}}{2}\)
\( \Rightarrow \) Chu kì lúc sau giảm 2 lần
Chọn D.
Câu 31:
Phương pháp giải:
Sử dụng biểu thức xác định số điểm dao động cực đại giữa hai nguồn cùng pha: \( - \frac{l}{\lambda } < k < \frac{l}{\lambda }\)
Lời Giải:
Số điểm dao động cực đại giữa hai nguồn: \( - \frac{l}{\lambda } < k < \frac{l}{\lambda }\)
\( \Leftrightarrow - \frac{{16}}{3} < k < \frac{{16}}{3} \\\Leftrightarrow - 5,3 < k < 5,3 \\\Rightarrow k = \pm 5; \pm 4;...; \pm 1,0\)
\( \Rightarrow \) Có 11 điểm dao động với biên độ cực đại
Chọn C.
Câu 32:
Phương pháp giải:
Sử dụng biểu thức tính cơ năng: \({\rm{W}} = \frac{1}{2}mgl\alpha _0^2\)
Lời Giải:
Cơ năng của con lắc đơn: \({\rm{W}} = \frac{1}{2}mgl\alpha _0^2 = \frac{1}{2}.9,8.0,09.1.{\left( {\frac{{6\pi }}{{180}}} \right)^2}\\ = 4,{84.10^{ - 3}}J\)
Chọn D.
Câu 33:
Phương pháp giải:
Sử dụng biểu thức chiều dài sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}\)
Lời Giải:
Sóng dừng trên dây hai đầu cố định: \({l_0} = k\frac{\lambda }{2} = k\frac{v}{{2f}}\)\( \Rightarrow f = \frac{{kv}}{{2{l_0}}}\)
Để có sóng dừng trên dây thì tần số dao động nhỏ nhất\({f_{\min }} = \frac{v}{{2{l_0}}}\) (khi k= 1)
Chọn C.
Câu 34:
Phương pháp giải:
Vận dụng hiện tượng cộng hưởng cơ
Lời Giải:
Tốc độ để xe bị rung mạnh nhất khi chạy là: \(v = \frac{8}{{1,5}} = \frac{{16}}{3}m/s = 19,2km/h\)
Chọn A.
Câu 35:
Phương pháp giải:
+ Sử dụng biểu thức độc lập: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
+ Sử dụng vòng tròn lượng giác
+ Sử dụng công thức góc quét: \(\Delta \varphi = \omega \Delta t\)
Lời Giải:
+ \(\frac{T}{4} = 0,5s \Rightarrow T = 2s\)
+ Thời điểm ban đầu lực kéo về có giá trị cực đại
\( \Rightarrow \) Li độ của vật tại thời điểm ban đầu là \({x_0} = A\)
+ Khi \(v = \omega x\)
Ta có: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {x^2} + \frac{{{\omega ^2}{x^2}}}{{{\omega ^2}}} \\\Rightarrow {x^2} = \frac{{{A^2}}}{2} \Rightarrow \left| x \right| = \frac{A}{{\sqrt 2 }}\)
Trong 1 chu kì, vật có li độ x và vận tốc thỏa mãn \(v = \omega x\) 2 lần
Mà: \({t_{2018}} = {t_{2016}} + {t_2}\)
Ta có: \({t_{2016}} = \frac{{2016}}{2}T = 1008T\)
\({t_2}\) là thời điểm thứ 2 vật có li độ x và vận tốc thỏa mãn \(v = \omega x\)
Từ vòng tròn lượng giác ta có: \(\Delta \varphi = \frac{{3\pi }}{2} + \frac{\pi }{4}\)
Lại có: \(\Delta \varphi = \omega .{t_2} \Rightarrow {t_2} = \frac{{\Delta \varphi }}{\omega } = \frac{{7\pi }}{{4.2\pi }}T = \frac{{7T}}{8}\)
\( \Rightarrow {t_{2018}} = {t_{2016}} + {t_2} = 1008T + \frac{{7T}}{8} \\= 2017,75s\)
Chọn C.
Câu 36:
Phương pháp giải:
+ Sử dụng biểu thức tính tần số góc \(\omega = \sqrt {\frac{k}{m}} \)
+ Sử dụng biểu thức tính độ giảm biên độ sau mỗi chu kì: \(\Delta A = \frac{{4\mu mg}}{k}\)
+ Tốc độ cực đại: \({v_{max}} = A\omega \)
Lời Giải:
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{20}}{{0,04}}} = 10\sqrt 5 \left( {rad/s} \right)\)
+ \(\mu = 0,2\)
+ Biên độ ban đầu của vật: \({A_0} = 6cm = 0,06m\)
Khi đó, tốc độ lớn nhất của vật đạt được trong quá trình dao động là tại vị trí cân bằng lần đầu tiên.
Độ giảm biên độ mỗi lần qua vị trí cân bằng: \(\Delta {A_1} = \frac{{\mu mg}}{k} = \frac{{0,2.0,04.10}}{{20}} = {4.10^{ - 3}}m\)
Khi đó, tốc độ lớn nhất của vật \({v_{max}} = \omega \left( {{A_0} - \Delta {A_1}} \right) \\= 10\sqrt 5 \left( {0,06 - {{4.10}^{ - 3}}} \right) = 1,25m/s\)
Chọn C.
Câu 37:
Phương pháp giải:
+ Sử dụng biểu thức tính cường độ âm: \(I = \frac{P}{{4\pi {r^2}}}\)
+ Sử dụng hệ thức lượng trong tam giác
Lời Giải:
Ta có: \({I_A} = {I_B} = I\) \( \Rightarrow OA = OB\)
Tại C cường độ âm cực đại \( \Rightarrow C\) gần O nhất\( \Rightarrow OC \bot AB\)
Lại có: \(\frac{{{I_C}}}{{{I_A}}} = \frac{{O{A^2}}}{{O{C^2}}} = \frac{9}{1} \Rightarrow OA = 3OC\)
Xét tam giác vuông \(OCA\) có:
\(O{A^2} = O{C^2} + A{C^2} \Leftrightarrow 9O{C^2} \\= O{C^2} + \frac{{A{B^2}}}{4} \Rightarrow OC = \frac{{AB\sqrt 2 }}{8} = 4cm\)
Chọn A.
Câu 38:
Phương pháp giải:
+ Sử dụng biểu thức tính cơ năng: \({\rm{W}} = \frac{1}{2}k{A^2} = {{\rm{W}}_d} + {{\rm{W}}_t}\)
+ Vận dụng biểu thức tính thế năng: \({{\rm{W}}_t} = \frac{1}{2}k{x^2}\)
+ Vận dụng trục thời gian suy ra từ vòng tròn lượng giác
Lời Giải:
+ Cơ năng: \({\rm{W}} = 0,1J\)
+ Tại vị trí có \({{\rm{W}}_d}_1 = 25mJ \Rightarrow {{\rm{W}}_{{t_1}}} = {\rm{W}} - {{\rm{W}}_{{d_1}}} \\= 0,075J\)
\( \Rightarrow \frac{{{{\rm{W}}_{{t_1}}}}}{{\rm{W}}} = \frac{{x_1^2}}{{{A^2}}} = \frac{3}{4} \Rightarrow \left| {{x_1}} \right| = \frac{{A\sqrt 3 }}{2}\)
+ Tại vị trí có \({{\rm{W}}_{{d_2}}} = 75mJ \Rightarrow {{\rm{W}}_{{t_2}}} = {\rm{W}} - {{\rm{W}}_{{d_2}}}\\ = 0,025J\)
\( \Rightarrow \frac{{{{\rm{W}}_{{t_2}}}}}{{\rm{W}}} = \frac{{x_2^2}}{{{A^2}}} = \frac{1}{4} \Rightarrow \left| {{x_2}} \right| = \frac{A}{2}\)
Động năng tăng từ giá trị \({{\rm{W}}_{{d_1}}}\) đến cực đại rồi giảm về \({{\rm{W}}_{{d_2}}}\)
\( \Rightarrow \) Vật đi từ vị trí \({x_1} = - \frac{{A\sqrt 3 }}{2}\) đến \(x = 0\) (VTCB) rồi đến vị trí \(x = \frac{A}{2}\)
Thời gian tương ứng là:
\(\Delta t = \frac{T}{6} + \frac{T}{{12}} = \frac{T}{4} = \frac{\pi }{{20}} \Rightarrow T = \frac{\pi }{5}s \Rightarrow \omega = \frac{{2\pi }}{T} \\= 10\left( {rad/s} \right)\)
Lại có: \({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}{A^2} \Rightarrow A = \sqrt {\frac{{2W}}{{m{\omega ^2}}}}\\ = 0,1m = 10cm\)
Chọn D.
Câu 39:
Phương pháp giải:
+ Sử dụng điều kiện sóng dừng trên dây hai đầu cố định: \(l = k\frac{\lambda }{2}\)
+ Sử dụng biểu thức tính biên độ sóng dừng: \({A_d} = 2A\sin \frac{{2\pi d}}{\lambda }\)
+ Sử dụng biểu thức tính biên độ bụng sóng: \({A_b} = 2A\)
Lời Giải:
Ta có sóng dừng trên dây 2 đầu cố định, khi đó: \(l = k\frac{\lambda }{2} \Leftrightarrow 24 = 2\frac{\lambda }{2} \Rightarrow \lambda = 24cm\)
\(MN = \frac{{24}}{3} = 8cm\)
Ta có M và N cách nút gần nhất một đoạn \(d = 4cm\)
+ Biên độ dao động tại M và N là: \({A_M} = {A_N} = 2A\sin \frac{{2\pi .4}}{{24}} = A\sqrt 3 \)
+ M, N nằm trên 2 bó sóng khác nhau nên chúng luôn dao động ngược pha
Ta có:
+ Khoảng cách nhỏ nhất giữa M và N là khi chúng cùng đi qua vị trí cân bằng: \({d_{\min }} = MN = 8cm\)
+ Khoảng cách lớn nhất giữa M và N là khi chúng ở 2 biên \({d_{max}} = \sqrt {M{N^2} + {{\left( {{A_M} + {A_N}} \right)}^2}} \\ = \sqrt {{8^2} + {{\left( {2A\sqrt 3 } \right)}^2}} \)
Theo đề bài, ta có: \(\frac{{{d_{max}}}}{{{d_{\min }}}} = 1,25\) \( \Leftrightarrow \frac{{\sqrt {{8^2} + 12{A^2}} }}{8} = 1,25 \Rightarrow A = \sqrt 3 cm\)
Biên độ dao động tại bụng sóng: \({A_b} = 2A = 2\sqrt 3 cm\)
Chọn D.
Câu 40:
Phương pháp giải:
+ Sử dụng hệ thức trong tam giác vuông
+ Viết phương trình sóng
+ Sử dụng điều kiện cùng pha: \(\Delta \varphi = k2\pi \)
+ Số điểm dao động cực tiểu giữa hai nguồn cùng pha: \( - \frac{l}{\lambda } - \frac{1}{2} < k < \frac{l}{\lambda } - \frac{1}{2}\)
Lời Giải:
Ta có:
+ Khoảng cách từ M đến A là \(d = \sqrt {{{\left( {4\sqrt 5 } \right)}^2} + {8^2}} = 12cm\)
+ Phương trình dao động tại I là \({u_I} = Acos\left( {\omega t - \frac{{2\pi .8}}{\lambda }} \right)cm\)
Phương trình dao động tại M là \({u_M} = Acos\left( {\omega t - \frac{{2\pi .12}}{\lambda }} \right)cm\)
Theo đề bài, ta có M là điểm gần I nhất và dao động cùng pha với I, nên ta có:
\(\Delta \varphi = \frac{{2\pi .12}}{\lambda } - \frac{{2\pi .8}}{\lambda } = 2\pi \Rightarrow \lambda = 4cm\)
Số điểm cực tiểu trên AB thỏa mãn:
\(\begin{array}{l} - \frac{l}{\lambda } - \frac{1}{2} < k < \frac{l}{\lambda } - \frac{1}{2}\\ \Leftrightarrow - \frac{{16}}{4} - \frac{1}{2} < k < \frac{{16}}{4} - \frac{1}{2}\\ \Rightarrow - 4,5 < k < 3,5\\ \Rightarrow k = - 4; \pm 3;...;0\end{array}\)
\( \Rightarrow \) Điểm N không dao động nằm trên đường thẳng vuông góc với AB tại A
\(A{N_{\min }}\) tương ứng với N là cực tiểu bậc 4 (ứng với \(k = - 4\))
Khi đó: \(AN - BN = \left( {2.\left( { - 4} \right) + 1} \right)\frac{\lambda }{2} = - 14cm\) (1)
Và \(B{N^2} = A{N^2} + A{B^2}\) (2)
Từ (1) và (2) ta có: \({\left( {AN + 14} \right)^2} = A{N^2} + {16^2} \Rightarrow AN = 2,14cm\)
Chọn A.
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra giữa học kì 1 Vật lí 12 - Đề số 02 có lời giải chi tiết timdapan.com"