Đề kiểm tra giữa học kì 1 Toán 7 - Đề số 4 - Cánh diều
I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Đề bài
I. TRẮC NGHIỆM ( 3 điểm)
Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Câu 1: Tìm phát biểu đúng trong các phát biểu sau:
A. \(\dfrac{2}{5} \in \mathbb{Z}\) B. \( - 5 \in \mathbb{N}\) C. \(\dfrac{{ - 5}}{4} \notin \mathbb{Q}\) D. \(\dfrac{3}{2} \in \mathbb{Q}\)
Câu 2: Tìm \(x\), biết: \(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)
A. \(x = \dfrac{{ - 3}}{8}\) B. \(x = \dfrac{3}{8}\) C. \(x = \dfrac{1}{2}\) D. \(x = - 1\)
Câu 3: Kết quả của phép tính: \(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\)
A. \(0,24\) B. \(0\) C. \(0,12\) D. \(0,2\)
Câu 4: Cho hình vẽ bên dưới. Biết tia \(Oz\) là tia phân giác của \(\angle xOy\). Tính \(\angle xOy\).

A. \(\angle xOy = {56^0}\) B. \(\angle xOy = {121^0}\) C. \(\angle xOy = {112^0}\) D. \(\angle xOy = {100^0}\)
Câu 5: Trong các hình vẽ dưới đây, liệt kê tất cả các hình là hình lăng trụ đứng tam giác hoặc hình lăng trụ đứng tứ giác?

A. Tất cả 6 hình B. Hình a), c), e), f) C. Hình b), c), d) D. Hình b), d)
Câu 6:Một hình lập phương có thể tích là \(343{m^3}\). Diện tích xung quanh của hình lập phương đó là:
A. \(343{m^2}\) B. \(98{m^2}\) C. \(196{m^2}\) D. \(240{m^2}\)
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính:
a) \(\dfrac{{13}}{{50}}.\left( { - 15,5} \right) - \dfrac{{13}}{{50}}.84\dfrac{1}{2}\) b) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.\left( { - 0,5} \right)\)
c) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( {\dfrac{{ - 1}}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\) d) \(\dfrac{{{{\left( { - 0,7} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{{{\left( {\dfrac{{ - 7}}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{\left( { - 1} \right)}^5}}}\)
Bài 2: (1 điểm)
a) Sắp xếp các số sau theo thứ tự tăng dần: \(6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {46} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - \sqrt {81} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} - 3,6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 2.\sqrt {16} \).
b) Sắp xếp các số sau theo thứ tự giảm dần: \(\sqrt {78} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {50 + 4} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 8{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 3.\sqrt {0,25} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} \).
Bài 3: (2,0 điểm)
Tìm \(x\), biết:
a) \({\left( {\dfrac{4}{5}} \right)^6}.x = {\left( {\dfrac{4}{5}} \right)^7}\) b) \({\left( {0,03} \right)^3}:x = - {\left( {0,03} \right)^2}\)
c) \(\sqrt {0,16} + x = 3.\sqrt {0,09} .2\dfrac{1}{3}\) d) \(\sqrt {0,25} - 3x - \sqrt {0,49} .\dfrac{1}{7} = \sqrt {0,04} .\dfrac{1}{2}\)
Bài 4: (1,0 điểm)
Một giá đình xây bể chứa nước hình lăng trụ đứng, phần trong lòng bể có đáy là hình vuông cạnh 1,5m, chiều cao bể là 1m. Sau đó họ dùng các viên gạch men kịch thước \(20 \times 30\)cm, dày 1cm để ốp xung quanh bể và đáy bể. Hỏi gia đình đó cần ít nhất bao nhiêu viên gạch ốp và sau khi ốp bể chứa được khoảng bao nhiêu lít nước?
Bài 5: (1,0 điểm)
Cho \(\angle xOy = {30^0}\), vẽ góc \(\angle xOt = {70^0}\) sao cho tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot\).
a) Tính \(\angle yOt?\) Tia \(Oy\) có là tia phân giác của góc \(\angle xOy\) không? Vì sao?
b) Gọi tia \(Om\) là tia đối của tia \(Ox\). Tính số đo của \(\angle mOt?\)
c) Gọi \(Oz\) là tia phân giác của \(\angle mOt\). Tính số đo của \(\angle yOz?\)
Lời giải
- TRẮC NGHIỆM ( 3 điểm)
|
1.A |
2.A |
3.B |
4.C |
5.A |
6.A |
Câu 1:
Phương pháp:
Tập hợp các số tự nhiên được kí hiệu là: \(\mathbb{N}\)
Tập hợp các số nguyên được kí hiệu là: \(\mathbb{Z}\)
Tập hợp các số hữu tỉ được kí hiệu là: \(\mathbb{Q}\).
Cách giải:
+ \(\dfrac{2}{5} \in \mathbb{Z}\) là sai vì \(\dfrac{2}{5} \in \mathbb{Q}\) nên loại đáp án A.
+ \( - 5 \in \mathbb{N}\) là sai vì \( - 5 \in \mathbb{Z}\) hoặc \( - 5 \in \mathbb{Q}\) nên loại đáp án B.
+ \(\dfrac{{ - 5}}{4} \notin \mathbb{Q}\) là sai vì \(\dfrac{{ - 5}}{4} \in \mathbb{Q}\) nên loại đáp án C.
+ \(\dfrac{3}{2} \in \mathbb{Q}\) là đúng nên chọn đáp án D.
Chọn A.
Câu 2:
Phương pháp:
Vận dụng quy tắc chuyển vế tìm giá trị của \(x\).
Cách giải:
\(\dfrac{1}{2} - \dfrac{2}{3}x = \dfrac{1}{4}\)
\(\begin{array}{l}\dfrac{2}{3}x = \dfrac{1}{2} - \dfrac{1}{4}\\\dfrac{2}{3}x = \dfrac{2}{4} - \dfrac{1}{4}\\\dfrac{2}{3}x = \dfrac{{ - 1}}{4}\\x = \dfrac{{ - 1}}{4}:\dfrac{2}{3}\\x = \dfrac{{ - 1}}{4}.\dfrac{3}{2}\\x = \dfrac{{ - 3}}{8}\end{array}\)
Vậy \(x = \dfrac{{ - 3}}{8}\)
Chọn A.
Câu 3:
Phương pháp:
Thực hiện tính toán với biểu thức có chứa căn bậc hai.
Cách giải:
\(\sqrt {1,44} - 2.{\left( {\sqrt {0,6} } \right)^2}\)
\(\begin{array}{l} = 1,2 - 2.0,6\\ = 1,2 - 1,2\\ = 0\end{array}\)
Chọn B.
Câu 4:
Phương pháp:
Vận dụng định nghĩa tia phân giác của một góc.
Cách giải:
Vì \(Oz\) là tia phân giác của \(\angle xOy\) nên ta có: \(\angle xOy = 2\angle xOz = {2.56^0} = {112^0}\)
Vậy \(\angle xOy = {112^0}\)
Chọn C.
Câu 5:
Phương pháp:
Hình lăng trụ đứng tam giác là hình hai mặt đáy là hình tam giác song song với nhau, ba mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Hình lăng trụ đứng tứ giác là hình hai mặt đáy là hình tứ giác song song với nhau, bốn mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Cách giải:
Từ các hình đã cho, ta thấy:
+ Hình vẽ b), c) là hình lăng trụ đứng tứ giác.
+ Hình vẽ d) là hình lăng trụ đứng tam giác.
Vậy hình vẽ b), c) và d) là các hình lăng trụ đứng tam giác hoặc lăng trụ đứng tứ giác.
Chọn A.
Câu 6:
Phương pháp:
Thể tích của hình lập phương có cạnh là \(a\) được tính theo công thức: \(V = {a^3}\).
Diện tích xung quanh của hình lập phương có cạnh là \(a\) được tính theo công thức: \({S_{xq}} = 4{a^2}\)
Cách giải:
Gọi cạnh của hình lập phương là \(a\,\left( m \right)\) (điều kiện: \(a > 0\))
Vì hình lập phương có thể tích là \(343{m^3}\) nên ta có: \({a^3} = 343 \Rightarrow {a^3} = {7^3} \Rightarrow a = 7\,\left( {tm} \right)\)
Diện tích xung quanh của hình lập phương là: \({S_{xq}} = {4.7^2} = 4.49 = 196\,\left( {{m^2}} \right)\)
Chọn A.
Phần II. Tự luận:
Bài 1:
Phương pháp:
a), b) Thực hiện phép cộng, trừ nhân chia số hữu tỉ.
c), d) Thực hiện phép tính có lũy thừa của một số hữu tỉ.
Chú ý: \({\left( {\dfrac{x}{y}} \right)^n} = \dfrac{{{x^n}}}{{{y^n}}}\left( {y \ne 0} \right)\)
\(\dfrac{{{x^m}}}{{{x^n}}} = {x^m}:{x^n} = {x^{m - n}}\)\(\left( {x \ne 0;m,n \in {\mathbb{N}^*}} \right)\)
Cách giải:
a) \(\dfrac{{13}}{{50}}.\left( { - 15,5} \right) - \dfrac{{13}}{{50}}.84\dfrac{1}{2}\)
\(\begin{array}{l} = \dfrac{{13}}{{50}}.\left( { - 15,5 - 84\dfrac{1}{2}} \right)\\ = \dfrac{{13}}{{50}}.\left( {\dfrac{{ - 31}}{2} - \dfrac{{169}}{2}} \right)\\ = \dfrac{{13}}{{50}}.\dfrac{{\left( { - 200} \right)}}{2}\\ = - 26\end{array}\)
b) \(\dfrac{2}{9} + \dfrac{1}{3}:\left( { - \dfrac{3}{2}} \right) + \dfrac{1}{2}.\left( { - 0,5} \right)\)
\(\begin{array}{l} = \dfrac{2}{9} + \dfrac{1}{3}.\left( { - \dfrac{2}{3}} \right) + \dfrac{1}{2}.\left( {\dfrac{{ - 1}}{2}} \right)\\ = \dfrac{2}{9} + \dfrac{{ - 2}}{9} + \dfrac{{ - 1}}{4}\\ = \left( {\dfrac{2}{9} + \dfrac{{ - 2}}{9}} \right) + \dfrac{{ - 1}}{4}\\ = 0 + \dfrac{{ - 1}}{4}\\ = \dfrac{{ - 1}}{4}\end{array}\)
c) \(4.{\left( { - \dfrac{1}{2}} \right)^3} - 2.{\left( {\dfrac{{ - 1}}{2}} \right)^2} + 3.\left( { - \dfrac{1}{2}} \right) + 1\)
\(\begin{array}{l} = 4.\dfrac{{{{\left( { - 1} \right)}^3}}}{{{2^3}}} - 2.\dfrac{{{{\left( { - 1} \right)}^2}}}{{{2^2}}} + \dfrac{{ - 3}}{2} + 1\\ = 4.\dfrac{{ - 1}}{8} - 2.\dfrac{1}{4} + \dfrac{{ - 3}}{2} + 1\\ = \dfrac{{ - 1}}{2} - \dfrac{1}{2} + \dfrac{{ - 3}}{2} + \dfrac{2}{2}\\ = \dfrac{{ - 1 - 1 + \left( { - 3} \right) + 2}}{2}\\ = \dfrac{{ - 3}}{2}\end{array}\)
d) \(\dfrac{{{{\left( { - 0,7} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{{{\left( {\dfrac{{ - 7}}{3}} \right)}^3}.{{\left( {\dfrac{3}{2}} \right)}^4}.{{\left( { - 1} \right)}^5}}}\)
\(\begin{array}{l} = \dfrac{{{{\left( {\dfrac{{ - 7}}{{10}}} \right)}^2}.{{\left( { - 5} \right)}^3}}}{{\dfrac{{{{\left( { - 7} \right)}^3}}}{{{3^3}}}.\dfrac{{{3^4}}}{{{2^4}}}.\left( { - 1} \right)}} = \dfrac{{\dfrac{{{{\left( { - 7} \right)}^2}}}{{{{\left( {2.5} \right)}^2}}}.{{\left( { - 1.5} \right)}^3}}}{{{{\left( { - 7} \right)}^3}.\dfrac{3}{{{2^4}}}.\left( { - 1} \right)}}\\ = \dfrac{{\dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}}}{{\dfrac{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}{{{2^4}}}}} = \dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}:\dfrac{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}{{{2^4}}}\\ = \dfrac{{{{\left( { - 7} \right)}^2}.{{\left( { - 1} \right)}^3}{{.5}^3}}}{{{2^2}{{.5}^2}}}.\dfrac{{{2^4}}}{{{{\left( { - 7} \right)}^3}.3.\left( { - 1} \right)}}\\ = \dfrac{1}{{\left( { - 7} \right)}}.\dfrac{{{{\left( { - 1} \right)}^2}}}{1}.\dfrac{5}{1}.\dfrac{{{2^2}}}{1}.\dfrac{1}{3}\\ = \dfrac{{5.4}}{{\left( { - 7} \right).3}} = \dfrac{{20}}{{ - 21}} = \dfrac{{ - 20}}{{21}}\end{array}\)
Bài 2:
Phương pháp:
Tính căn bậc hai số học của các căn bậc hai, sau đó so sánh.
Cách giải:
a) \(6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {46} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - \sqrt {81} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} - 3,6{\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 2.\sqrt {16} \)
+ Vì \(36 < 46 < 49\) nên \(\sqrt {36} {\rm{\;}} < \sqrt {46} {\rm{\;}} < \sqrt {49} \) hay \(6 < \sqrt {46} {\rm{\;}} < 7\)
\(2.\sqrt {16} {\rm{\;}} = 2.\sqrt {{4^2}} {\rm{\;}} = 2.4 = 8 > 7\)
Suy ra, \(0 < 6 < \sqrt {46} {\rm{\;}} < 2.\sqrt {16} \) (1)
+ Ta có: \( - \sqrt {81} {\rm{\;}} = {\rm{\;}} - \sqrt {{9^2}} {\rm{\;}} = {\rm{\;}} - 9\)
Vì \(3,6 < 9\) nên \( - 3,6 > {\rm{\;}} - 9\) suy ra \( - 3,6 > {\rm{\;}} - \sqrt {81} \)
Suy ra, \(0 > {\rm{\;}} - 3,6 > {\rm{\;}} - \sqrt {81} \) (2)
Từ (1) và (2), suy ra \( - \sqrt {81} {\kern 1pt} {\kern 1pt} < {\kern 1pt} - 3,6{\kern 1pt} {\kern 1pt} < {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} < {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} < {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {46} {\kern 1pt} {\kern 1pt} < {\kern 1pt} {\kern 1pt} {\kern 1pt} 2.\sqrt {16} \)
Vậy thứ tự tăng dần của các số là: \( - \sqrt {81} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 3,6{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {46} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 2.\sqrt {16} \).
b) \(\sqrt {78} {\kern 1pt} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {50 + 4} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 8{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 3.\sqrt {0,25} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} \)
+ Vì \(64 < 78\) nên \(\sqrt {64} {\rm{\;}} < \sqrt {78} \) hay \(8 < \sqrt {78} \)
Ta có: \(\sqrt {50 + 4} {\rm{\;}} = \sqrt {54} \)
Vì \(49 < 54 < 64\) nên \(\sqrt {49} {\rm{\;}} < \sqrt {54} {\rm{\;}} < \sqrt {64} \) hay \(7 < \sqrt {54} {\rm{\;}} < 8\)
Vì \(0 < 6 < 7 < \sqrt {54} {\rm{\;}} < 8 < \sqrt {78} \) nên \(0 < 6 < \sqrt {54} {\rm{\;}} < \sqrt {78} \) (1)
Suy ra, \(0 < 6 < \sqrt {50 + 4} {\rm{\;}} < \sqrt {78} \)
+ Ta có: \( - 3.\sqrt {0,25} {\rm{\;}} = {\rm{\;}} - 3.\sqrt {0,{5^2}} {\rm{\;}} = {\rm{\;}} - 3.0,5 = {\rm{\;}} - 3.\dfrac{1}{2} = {\rm{\;}} - \dfrac{3}{2} = {\rm{\;}} - 1,5\)
Vì \(1,5 < 8\) nên \( - 1,5 > {\rm{\;}} - 8\)
Suy ra, \(0 > {\rm{\;}} - 3.\sqrt {0,25} {\rm{\;}} - 8\) (2)
Từ (1) và (2), suy ra \( - 8 < {\rm{\;}} - 3.\sqrt {0,25} {\rm{\;}} < 0 < 6 < \sqrt {50 + 4} {\rm{\;}} < \sqrt {78} \)
Vậy thứ tự giảm dần của các số là: \(\sqrt {78} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} \sqrt {50 + 4} {\kern 1pt} {\kern 1pt} {\rm{\;}};{\kern 1pt} {\kern 1pt} 6{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 3\sqrt {0,25} {\kern 1pt} {\kern 1pt} ;{\kern 1pt} {\kern 1pt} - 8\).
Bài 3:
Phương pháp:
Thực hiện phép tính, vận dụng quy tắc chuyển vế tìm \(x\)
Cách giải:
a) \({\left( {\dfrac{4}{5}} \right)^5}.x = {\left( {\dfrac{4}{5}} \right)^7}\)
\(\begin{array}{l}x = {\left( {\dfrac{4}{5}} \right)^7}:{\left( {\dfrac{4}{5}} \right)^5}\\x = {\left( {\dfrac{4}{5}} \right)^{7 - 5}} = {\left( {\dfrac{4}{5}} \right)^2}\\x = \dfrac{{{4^2}}}{{{5^2}}} = \dfrac{{16}}{{25}}\end{array}\)
Vậy \(x = \dfrac{{16}}{{25}}\)
b) \({\left( {0,03} \right)^3}:x = - {\left( {0,03} \right)^2}\)
\(\begin{array}{l}x = {\left( {0,03} \right)^3}:\left[ { - {{\left( {0,03} \right)}^2}} \right]\\x = - \left[ {{{\left( {0,03} \right)}^3}:{{\left( {0,03} \right)}^2}} \right]\\x = - {\left( {0,03} \right)^{3 - 2}}\\x = - 0,03\end{array}\)
Vậy \(x = - 0,03\)
c) \(\sqrt {0,16} + x = 3.\sqrt {0,09} .2\dfrac{1}{3}\)
\(\begin{array}{l}0,4 + x = 3.0,3.\dfrac{7}{3}\\0,4 + x = 0,3.7\\0,4 + x = 2,1\\x = 2,1 - 0,4\\x = 1,7\end{array}\)
Vậy \(x = 1,7\)
d) \(\sqrt {0,25} - 3x - \sqrt {0,49} .\dfrac{1}{7} = \sqrt {0,04} .\dfrac{1}{2}\)
\(\begin{array}{l}0,5 - 3x - 0,7.\dfrac{1}{7} = 0,2.\dfrac{1}{2}\\0,5 - 3x - 0,1 = 0,1\\0,4 - 3x = 0,1\\3x = 0,4 - 0,1\\3x = 0,3\\x = 0,3:3\\x = 0,1\end{array}\)
Vậy \(x = 0,1\)
Bài 4:
Phương pháp:
+ Tính diện tích: đáy bể, xung quanh bể và diện tích một viên gạch
Thực hiện phép chia ước lượng được số viên gạch cần ốp
+ Tính chiều dài cạnh đáy, chiều cao của bể sau khi ốp gạch
Tính thể tích sau khi ốp gạch
Cách giải:
* Diện tích đáy của bể là: \(1,5.1,5 = 2,25\,\left( {{m^2}} \right)\)
Diện tích xung quanh của bể là: \(4.1,5.1 = 6\,\left( {{m^2}} \right)\)
Diện tích của đáy bể và diện tích xung quanh của bể là: \(2,25 + 6 = 8,25\,\left( {{m^2}} \right)\)
Diện tích một viên gạch là: \(20.30 = 600\left( {c{m^2}} \right) = 0,06\left( {{m^2}} \right)\)
Ta có: \(8,25:0,06 = 137,5\)
Như vậy cần ít nhất \(138\) viên gạch ốp.
* Chiều dài cạnh đáy sau khi ốp gạch là: \(1,5 - 2.0,1 = 1,5 - 0,2 = 1,48\,\left( m \right)\)
Chiều cao của bể sau khi ốp gạch là: \(1 - 2.0,01 = 1 - 0,2 = 1,98\,\left( m \right)\)
Thể tích của bể sau khi ốp gạch là: \({\left( {1,48} \right)^2}.0,98 = 2,146592\,\left( {{m^3}} \right) = 2146,692\,\left( {d{m^3}} \right)\)
Vậy sau khi ốp bể, bể chứa được khoảng 2147 lít nước.
Bài 5:
Phương pháp:
Vận dụng tính chất tia phân giác của một góc
Vận dụng kiến thức của hai góc kề nhau.
Cách giải:
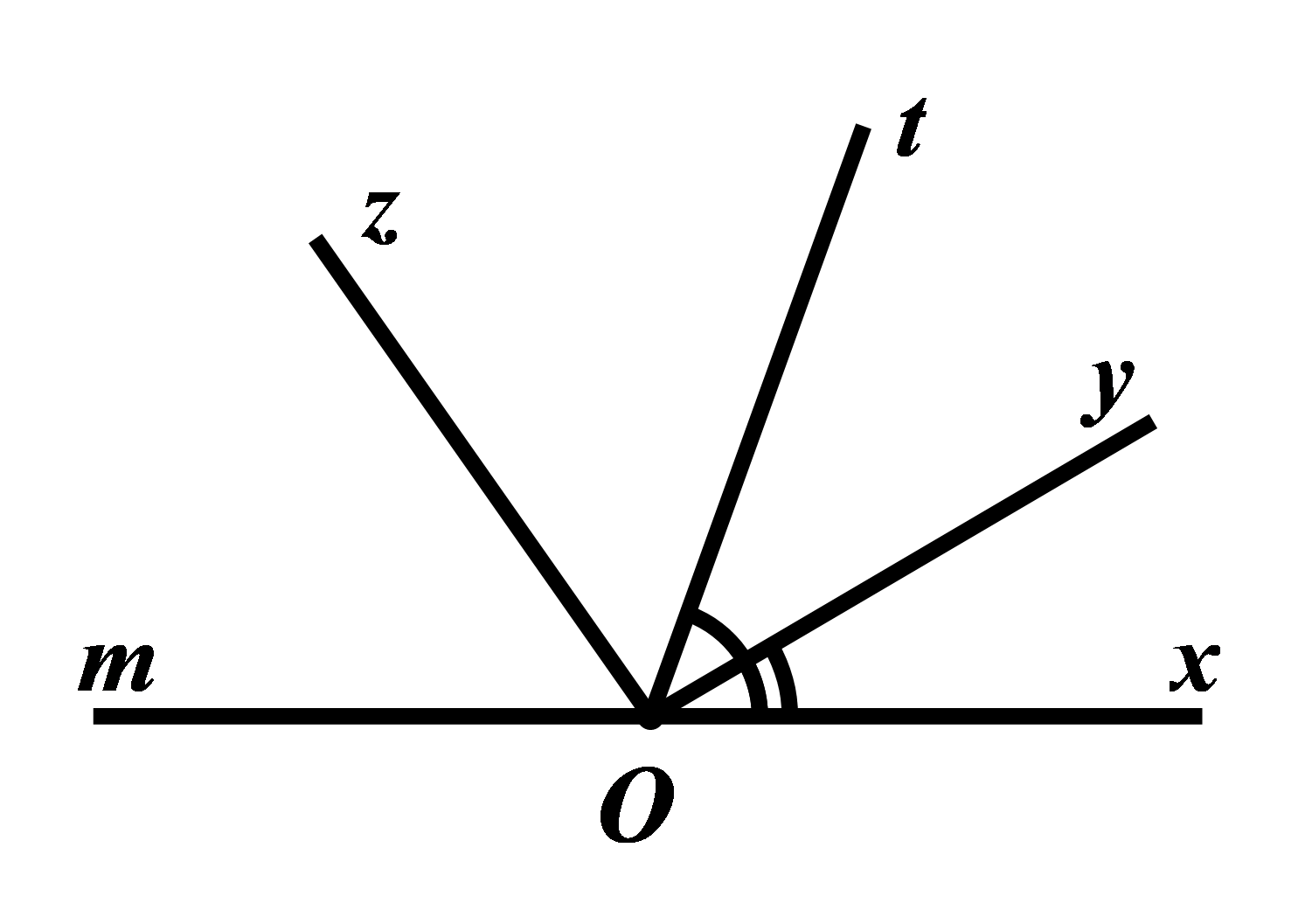
a) * Vì \(\angle xOy\) và \(\angle yOt\) là hai góc kề nhau nên ta có: \(\angle xOy + \angle yOt = \angle xOy\)
\(\begin{array}{l} \Rightarrow {30^0} + \angle yOt = {70^0}\\ \Rightarrow \angle yOt = {70^0} - {30^0}\\ \Rightarrow \angle yOt = {40^0}\end{array}\)
Vậy \(\angle yOt = {40^0}\).
* Vì \(\angle xOy = {30^0};\angle yOt = {40^0}\) nên hai góc \(\angle xOy\) và \(\angle yOt\) không bằng nhau
Do đó, \(Oy\) không là tia phân giác của \(\angle xOt\).
b) Vì \(Om\) là tia đối của tia \(Ox\) nên \(\angle xOm\) là góc bẹt và bằng \({180^0}\).
Ta có: \(\angle xOt\) và \(\angle tOm\) là hai góc kề bù nên \(\angle xOt + \angle tOm = {180^0}\)
\(\begin{array}{l} \Rightarrow {70^0} + \angle tOm = {180^0}\\ \Rightarrow \angle tOm = {180^0} = {70^0}\\ \Rightarrow \angle tOm = {110^0}\end{array}\)
Vậy \(\angle tOm = {110^0}\)
c) Vì \(Oz\) là tia phân giác của \(\angle mOt\) (giả thiết) nên \(\angle zOt = \dfrac{1}{2}\angle mOt = \dfrac{1}{2}{.110^0} = {55^0}\)
Hai góc \(\angle yOt\) và \(\angle tOz\) kề nhau nên \(\angle yOt + \angle tOz = \angle yOz\)
\(\begin{array}{l} \Rightarrow {40^0} + {55^0} = \angle yOz\\ \Rightarrow {95^0} = \angle yOz\end{array}\)
Vậy \(\angle yOz = {95^0}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra giữa học kì 1 Toán 7 - Đề số 4 - Cánh diều timdapan.com"







