Đề kiểm tra giữa học kì 1 Toán 7 - Đề số 3 - Kết nối tri thức
I. TRẮC NGHIỆM ( 3 điểm) Chọn chữ cái A,B,C hoặc D đứng trước câu trả lời đúng.
Đề bài
Phần I: Trắc nghiệm (3 điểm). Hãy chọn phương án trả lời đúng và viết chữ cái đứng trước đáp án đó vào bài làm.
Câu 1: Số \(\dfrac{{ - 4}}{{ - 5}}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
A. 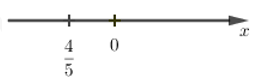
B. 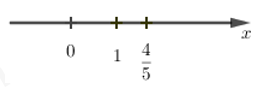
C. 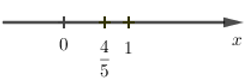
D. 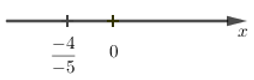
Câu 2: Số hữu tỉ x thoả mãn \(x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\) là:
A. \(\dfrac{5}{2}\) B. \(\dfrac{3}{{10}}\) C. \(\dfrac{7}{6}\) D. \(\dfrac{{ - 5}}{{17}}\)
Câu 3: Tính \( - 23,\left( 2 \right) + \dfrac{3}{7} + 13,\left( 2 \right) - \dfrac{{10}}{7}\) bằng:
A. \( - 9\). B. \( - 11,\left( 4 \right)\). C. \( - 11\). D. \( - 35,\left( 4 \right)\).
Câu 4: Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\angle xOy = \dfrac{2}{3}\angle xOy'\). Tính số đo \(\angle xOy'\)?
A. \({36^0}\) B. \({72^0}\) C. \({108^0}\) D. \({18^0}\)
Câu 5: Cho tia On là tia phân giác của \(\angle mOt\). Biết \(\angle mOn = {70^^\circ }\), số đo của \(\angle mOt\) là:
A. \({140^0}\) B. \({120^0}\) C. \({35^0}\) D. \({60^0}\)
Câu 6: Cho định lí: “Nếu hai đường thẳng song song cắt đường thẳng thứ ba thì hai góc đồng vị bằng nhau’ (xem hình vẽ dưới đây). Giả thiết của định lí là:
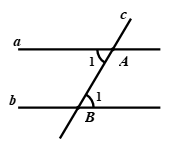
A. \(a//b,a \bot c\) B. \(a//b,c \cap a = \left\{ A \right\},c \cap b = \left\{ B \right\}\)
C. \(a//b,a//c\) D. \(a//b,c\) bất kì
Phần II. Tự luận (7 điểm):
Bài 1: (2,0 điểm)
Thực hiện phép tính hợp lí:
a) \(\dfrac{5}{{14}} - 3,7 - \dfrac{{19}}{{14}} + \dfrac{8}{9} - 6,3\) b) \(\dfrac{{11}}{{24}} - \dfrac{5}{{41}} + \dfrac{{13}}{{24}} + 0,5 - \dfrac{{36}}{{41}}\)
c) \(\dfrac{{{{2.6}^9} - {2^5}{{.18}^4}}}{{{2^2}{{.6}^8}}}\) d) \(\dfrac{{\sqrt {49} }}{{\sqrt 4 }} + \dfrac{{\sqrt {225} }}{{\sqrt {144} }} - 3,5\)
Bài 2: (2,0 điểm)
Tìm \(x,\) biết:
a) \( - \dfrac{2}{3} + 2\left( {x + \dfrac{1}{2}} \right) = 1\) b) \(\left( {2x - \dfrac{2}{3} + \dfrac{1}{2}x} \right)\left( {{x^2} + 5} \right) = 0\)
c) \({\left( {{5^x}} \right)^2} = {25^{11}}\) d) \(\dfrac{3}{4}x + \sqrt {0,04} = \dfrac{1}{5}.\sqrt {0,25} \)
Bài 3: Bác Thu mua ba món hàng ở một siêu thị. Món hàng thứ nhất giá 125 000 đồng và được giảm giá 30%, món hàng thứ hai giá 300 000 đồng và được giảm giá 15%, món hàng thứ ba được giảm giá 12,5%. Tổng số tiền bác Thu phải thanh toán là 692 500 đồng. Hỏi giá tiền món hàng thứ ba lúc chưa giảm giá là bao nhiêu?
Bài 4: (1,0 điểm)
Tìm số đo của góc \(QRS\) trong hình vẽ bên dưới, biết \(aa'//bb'.\)

Bài 5: Tìm số nguyên \(x\) sao cho biểu thức sau là số nguyên: \(A = \dfrac{{\sqrt x + 5}}{{\sqrt x - 3}}\)
Lời giải
Phần I: Trắc nghiệm
|
1.C |
2.B |
3.C |
4.C |
5.A |
6.B |
Câu 1:
Phương pháp:
Cách biểu diễn số hữu tỉ trên trục số:
Nếu \(\dfrac{a}{b}\) là số hữu tỉ dương, ta chia khoảng có độ dài \(1\) đơn vị làm \(b\) phần bằng nhau, rồi lấy về phía chiều dương trục \(Ox\) là \(a\) phần, ta được vị trí số \(\dfrac{a}{b}\).
Cách giải:
Ta có: \(\dfrac{{ - 4}}{{ - 5}} = \dfrac{4}{5}\)
Ta biểu diễn trên trục số như sau:
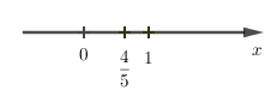
Chọn C.
Câu 2:
Phương pháp:
- Vận dụng quy tắc chuyển vế:
Chuyển vế \( \Rightarrow \) đổi dấu
+ \(x + y = z \Rightarrow x = z - y\)
+ \(x - y = z \Rightarrow x = z + y\)
Từ đó tìm được giá trị \(x\) thoả mãn
Cách giải:
Ta có: \(x - \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right) = \dfrac{9}{{20}}\)
\(\begin{array}{*{20}{l}}{x = \dfrac{9}{{20}} + \left( {\dfrac{5}{4} - \dfrac{7}{5}} \right)}\\{x = \dfrac{9}{{20}} + \dfrac{5}{4} - \dfrac{7}{5}}\\{x = \dfrac{9}{{20}} + \dfrac{{25}}{{20}} - \dfrac{{28}}{{20}}}\\{x = \dfrac{6}{{20}} = \dfrac{3}{{10}}}\end{array}\)
Vậy \(x = \dfrac{3}{{10}}\)
Chọn B.
Câu 3:
Phương pháp:
Nhóm các số hạng một cách hợp lý.
Cách giải:
Ta có: \( - 23,\left( 2 \right) + \dfrac{3}{7} + 13,\left( 2 \right) - \dfrac{{10}}{7} = \left[ { - 23,\left( 2 \right) + 13,\left( 2 \right)} \right] + \left( {\dfrac{3}{7} - \dfrac{{10}}{7}} \right) = \left( { - 10} \right) + \left( { - 1} \right) = {\rm{ \;}} - 11\)
Chọn C.
Câu 4:
Phương pháp:
Hai góc kề bù có tổng số đo là \({180^0}\).
Cách giải:
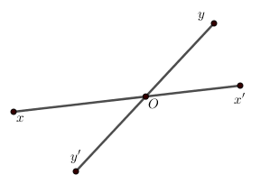
Vì \(\angle xOy\) và \(\angle x'Oy\) là hai góc kề bù nên \(\angle xOy + \angle x'Oy = {180^0}\)
Mà \(\angle xOy = \dfrac{2}{3}\angle x'Oy\)
Suy ra \(\dfrac{2}{3}\angle x'Oy + \angle xOy' = {180^0}\)
\(\dfrac{5}{3}\angle xOy' = {180^0}\)
\(\begin{array}{l}\angle xOy' = {180^0}:\dfrac{5}{3} = {180^0}.\dfrac{3}{5}\\\angle xOy' = {108^0}\end{array}\)
Vậy \(\angle xOy' = {108^0}\)
Chọn C.
Câu 5:
Phương pháp:
Nếu tia \(Oz\) là tia phân giác của \(\angle xOy\) thì: \(\angle xOz = \angle yOz = \dfrac{1}{2}\angle xOy\)
Cách giải:
Vì \(On\) là tia phân giác của \(\angle mOt\) nên \(\angle mOn = \angle tOn = \dfrac{1}{2}\angle mOt\)
Suy ra \(\angle mOt = 2.\angle mOn = {2.70^0}{\rm{ \;}} = {140^0}\)
Chọn A.
Câu 6:
Phương pháp:
Giả thiết của định lí là điều cho biết của đề bài, kết luận của định lí là điều suy ra được.
Cách giải:
Giả thiết của định lí trên là: \(a//b,c \cap a = \left\{ A \right\},c \cap b = \left\{ B \right\}\)
Chọn B.
Phần II. Tự luận:
Bài 1:
Phương pháp:
a) + b) Đổi số thập phân sang phân số
Thực hiện các phép toán với số hữu tỉ.
c) Tích và thương của hai lũy thừa cùng cơ số:
+ Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ: \({x^m}.{x^n} = {x^{m + n}}\)
+ Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và lấy số mũ của lũy thừa bị chia trừ đi số mũ của lũy thừa chia: \({x^m}:{x^n} = {x^{m - n}}\,\left( {x \ne 0;m \ge n} \right)\)
Tích của lũy thừa cùng số mũ: \({x^m}.{y^m} = {\left( {x.y} \right)^m}\)
d) Tính căn bậc hai, đổi số thập phân sang phân số
Thực hiện các phép toán với số hữu tỉ.
Cách giải:
a) \(\dfrac{5}{{14}} - 3,7 - \dfrac{{19}}{{14}} + \dfrac{8}{9} - 6,3\)
\(\begin{array}{l} = \left( {\dfrac{5}{{14}} - \dfrac{{19}}{{14}}} \right) + \left( { - 3,7 - 6,3} \right) + \dfrac{8}{9}\\ = \dfrac{{ - 14}}{{14}} + \left( { - 10} \right) + \dfrac{8}{9}\\ = - 1 + \left( { - 10} \right) + \dfrac{8}{9}\\ = - 11 + \dfrac{8}{9} = \dfrac{{ - 99}}{9} + \dfrac{8}{9}\\ = \dfrac{{ - 91}}{9}\end{array}\)
b) \(\dfrac{{11}}{{24}} - \dfrac{5}{{41}} + \dfrac{{13}}{{24}} + 0,5 - \dfrac{{36}}{{41}}\)
\(\begin{array}{l} = \left( {\dfrac{{11}}{{24}} + \dfrac{{13}}{{24}}} \right) + \left( {\dfrac{{ - 5}}{{41}} - \dfrac{{ - 36}}{{41}}} \right) + \dfrac{1}{2}\\ = \dfrac{{24}}{{24}} + \dfrac{{ - 41}}{{41}} + \dfrac{1}{2}\\ = 1 + \left( { - 1} \right) + \dfrac{1}{2}\\ = 0 + \dfrac{1}{2} = \dfrac{1}{2}\end{array}\)
|
c) \(\dfrac{{{{2.6}^9} - {2^5}{{.18}^4}}}{{{2^2}{{.6}^8}}}\) \( = \dfrac{{{{2.6}^9} - {2^5}.{{\left( {3.6} \right)}^4}}}{{{2^2}{{.6}^8}}}\) \(\begin{array}{l} = \dfrac{{{{2.6}^9} - {2^5}{{.3}^4}{{.6}^4}}}{{{2^2}{{.6}^8}}}\\ = \dfrac{{{{2.6}^9} - 2.{{\left( {2.3} \right)}^4}{{.6}^4}}}{{{2^2}{{.6}^8}}}\\ = \dfrac{{{{2.6}^9} - {{2.6}^4}{{.6}^4}}}{{{2^2}{{.6}^8}}}\\ = \dfrac{{{{2.6}^9} - {{2.6}^8}}}{{{2^2}{{.6}^8}}}\\ = \dfrac{{{{2.6}^8}.\left( {6 - 1} \right)}}{{{{2.2.6}^8}}} = \dfrac{5}{2}\end{array}\) |
d) \(\dfrac{{\sqrt {49} }}{{\sqrt 4 }} + \dfrac{{\sqrt {225} }}{{\sqrt {144} }} - 3,5\) \( = \dfrac{{\sqrt {{7^2}} }}{{\sqrt {{2^2}} }} + \dfrac{{\sqrt {{{15}^2}} }}{{\sqrt {{{12}^2}} }} - 3,5\) \(\begin{array}{l} = \dfrac{7}{2} + \dfrac{{15}}{{12}} - \dfrac{7}{2}\\ = \left( {\dfrac{7}{2} - \dfrac{7}{2}} \right) + \dfrac{{15}}{{12}}\\ = 0 + \dfrac{{15}}{{12}} = \dfrac{{15}}{{12}} = \dfrac{5}{4}\end{array}\)
|
Bài 2:
Phương pháp:
a) Vận dụng quy tắc chuyển vế tìm \(x\)
b) \(A\left( x \right).B\left( x \right) = 0\)
Trường hợp 1: Giải \(A\left( x \right) = 0\)
Trường hợp 2: Giải \(B\left( x \right) = 0\)
c) Lũy thừa của một lũy thừa:
Khi tính lũy thừa của một lũy thừa, ta giữ nguyên cơ số và nhân hai số mũ: \({\left( {{x^m}} \right)^n} = {x^{m.n}}\)
\({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Rightarrow f\left( x \right) = g\left( x \right)\)
d) Tính căn bậc hai; Vận dụng quy tắc chuyển vế tìm \(x\)
Cách giải:
|
a) \( - \dfrac{2}{3} + 2\left( {x + \dfrac{1}{2}} \right) = 1\) \(\begin{array}{l}2\left( {x + \dfrac{1}{2}} \right) = 1 + \dfrac{2}{3} = \dfrac{3}{3} + \dfrac{2}{3}\\2\left( {x + \dfrac{1}{2}} \right) = \dfrac{5}{3}\\x + \dfrac{1}{2} = \dfrac{5}{3}:2\\x + \dfrac{1}{2} = \dfrac{5}{3}.\dfrac{1}{2} = \dfrac{5}{6}\\x = \dfrac{5}{6} - \dfrac{1}{2} = \dfrac{5}{6} - \dfrac{3}{6}\\x = \dfrac{2}{6} = \dfrac{1}{3}\end{array}\) Vậy \(x = \dfrac{1}{3}\)
|
b) \(\left( {2x - \dfrac{2}{3} + \dfrac{1}{2}x} \right)\left( {{x^2} + 5} \right) = 0\) Trường hợp 1: \(2x - \dfrac{2}{3} + \dfrac{1}{2}x = 0\) \(\begin{array}{l}\left( {2 + \dfrac{1}{2}} \right)x - \dfrac{2}{3} = 0\\\left( {\dfrac{4}{2} + \dfrac{1}{2}} \right)x = \dfrac{2}{3}\\\dfrac{5}{2}x = \dfrac{2}{3}\\x = \dfrac{2}{3}:\dfrac{5}{2} = \dfrac{2}{3}.\dfrac{2}{5}\\x = \dfrac{4}{{15}}\end{array}\) Trường hợp 2: \({x^2} + 5 = 0\) Vì \({x^2} \ge 0\) với mọi số thực \(x\). Nên \({x^2} + 5 \ge 5\) với mọi số thực \(x\). Suy ra \({x^2} + 5 > 0\) với mọi số thực \(x\). Do đó, không có \(x\) thỏa mãn \({x^2} + 5 = 0\). Vậy \(x = \dfrac{4}{{15}}\) |
|
c) \({\left( {{5^x}} \right)^2} = {25^{11}}\) \(\begin{array}{l}{5^{x.2}} = {\left( {{5^2}} \right)^{11}}\\{5^{2x}} = {5^{2.11}} = {5^{22}}\\ \Rightarrow 2x = 22\\\,\,\,\,\,\,\,\,\,\,x = 11\end{array}\) Vậy \(x = 11\)
|
d) \(\dfrac{3}{4}x + \sqrt {0,04} = \dfrac{1}{5}.\sqrt {0,25} \) \(\begin{array}{l}\dfrac{3}{4}x + \sqrt {{{\left( {0,2} \right)}^2}} = \dfrac{1}{5}.\sqrt {{{\left( {0,5} \right)}^2}} \\\dfrac{3}{4}x + 0,2 = \dfrac{1}{5}.0,5 = 0,1\\\dfrac{3}{4}x = 0,1 - 0,2\\\dfrac{3}{4}x = - 0,1 = \dfrac{{ - 1}}{{10}}\\x = \dfrac{{ - 1}}{{10}}:\dfrac{3}{4} = \dfrac{{ - 1}}{{10}}.\dfrac{4}{3}\\x = \dfrac{{ - 2}}{{15}}\end{array}\) Vậy \(x = \dfrac{{ - 2}}{{15}}\) |
Bài 3:
Phương pháp:
Tính tiền món hàng thứ nhất, thứ hai sau giảm
Tính tiền món hàng thứ ba sau giảm = tổng số tiền bác Thu thanh toán – (số tiền món hàng thứ nhất sau giảm + số tiền món hàng thứ hai sau giảm)
Số tiền món hàng thứ ba chưa giảm = số tiền sau giảm: (100% – % được giảm giá)
Cách giải:
Bác Thu mua món hàng thứ nhất với giá sau giảm là:
\(125\,000.\left( {100\% - 30\% } \right) = 87\,500\) (đồng)
Bác Thu mua món hàng thứ hai với giá sau giảm là:
\(300\,000.\left( {100\% - 15\% } \right) = 255\,000\) (đồng)
Món hàng thứ ba bác Thu mua với giá sau giảm là:
\(692\,500 - 87\,500 - 255\,000 = 350\,000\) (đồng)
Vì món hàng thứ ba bác Thu mua được giảm giá 12,5% nên giá ban đầu của món hàng là:
Bài 4:
Phương pháp:
Vận dụng dấu hiệu và tính chất của hai đường thẳng song song.
Vận dụng kiến thức của hai góc kề nhau.
Cách giải:
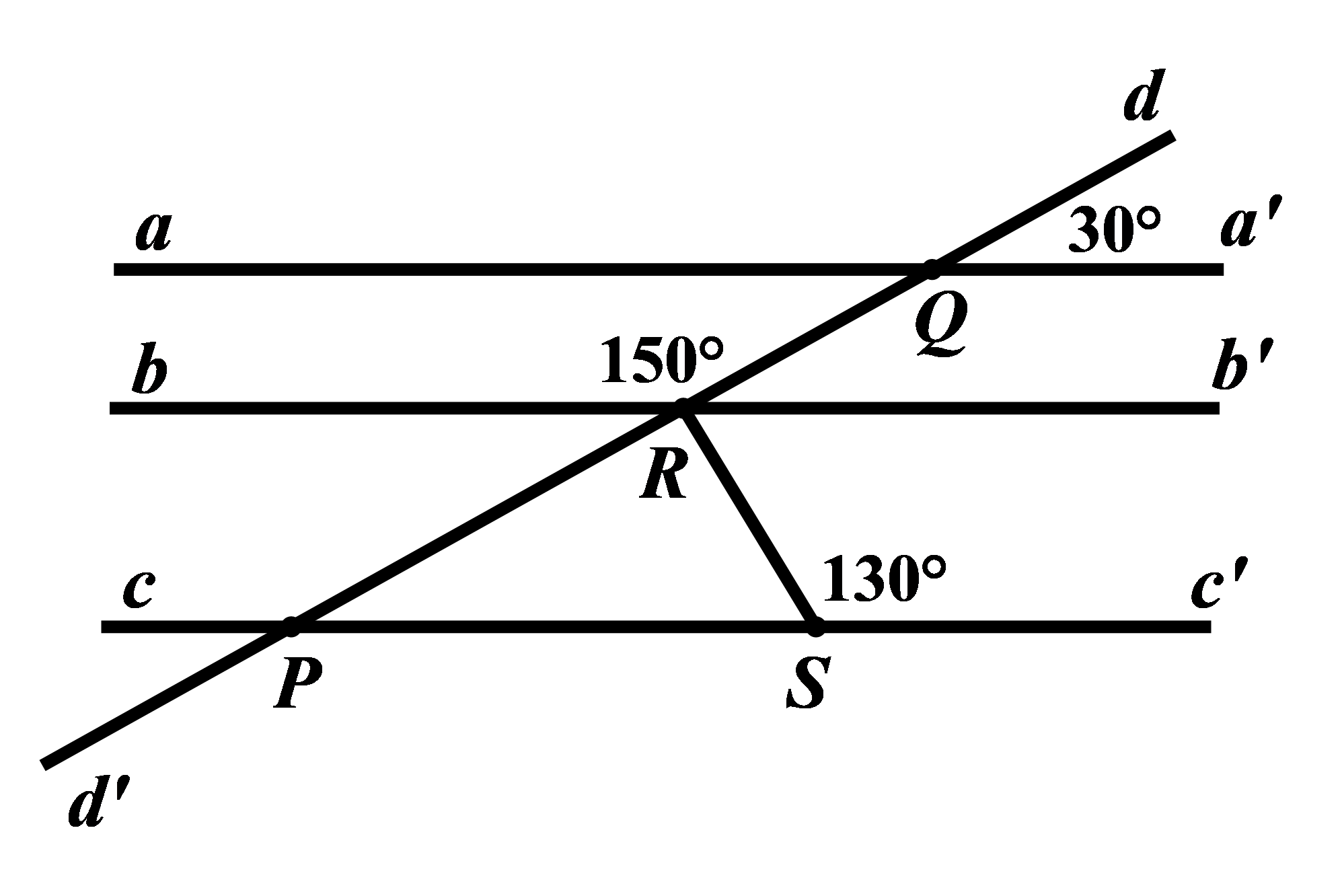
Kẻ \(Rb'\) là tia đối của tia \(Rb\)
Ta có: \(\angle QRb + \angle QRb' = {180^0}\) (hai góc kề bù) nên \(\angle QRb' = {180^0} - \angle QRb = {180^0} - {150^0} = {30^0}\)
Suy ra \(\angle dQa' = \angle QRb'\) (cùng bằng \({30^0}\)). Mà \(\angle dQa',\angle QRb'\) ở vị trí đồng bị nên \(aa'//bb'\).
Do \(aa'//bb'\) nên \(\angle dPc' = \angle dQa' = {30^0}\) (hai góc đồng vị). Vì vậy \(\angle dPc' = \angle QRb'\) (cùng bằng \({30^0}\)).
Mà \(\angle dPc',\angle QRb'\) ở vị trí đồng vị nên \(cc'//bb'\).
Suy ra \(\angle SRb' + \angle RSc' = {180^0}\) (hai góc trong cùng phía) hay \(\angle SRb' = {180^0} - \angle RSc' = {180^0} - {130^0} = {50^0}\)
Do hai góc \(QRb'\) và \(SRb'\) là hai góc kề nhau nên \(\angle QRS = \angle QRb' + \angle SRb' = {30^0} + {50^0} = {80^0}\)
Bài 5:
Phương pháp:
Để \(P = \dfrac{{M\left( x \right)}}{{n\left( x \right)}}\) có giá trị nguyên
+ Bước 1: Biến đổi \(P = m\left( x \right) + \dfrac{k}{{n\left( x \right)}}\). Trong đó \(k\) là số nguyên
+ Bước 2: Lập luận: Để \(P\) có giá trị nguyên thì \(k \vdots n\left( x \right)\) hay \(n\left( x \right) \in \)Ư\(\left( k \right)\)
+ Bước 3: Lập bảng giá trị và kiểm tra \(x\) với điều kiện đã tìm
+ Bước 4: Kết luận
Cách giải:
c) \(A = \dfrac{{\sqrt x + 5}}{{\sqrt x - 3}}\) (điều kiện: \(x \ge 0\))
\( = \dfrac{{\sqrt x - 3 + 8}}{{\sqrt x - 3}}\)
\(\begin{array}{l} = \dfrac{{\sqrt x - 3}}{{\sqrt x - 3}} + \dfrac{8}{{\sqrt x - 3}}\\ = 1 + \dfrac{8}{{\sqrt x - 3}}\end{array}\)
Để \(A \in \mathbb{Z}\) thì \(\dfrac{8}{{\sqrt x - 3}} \in \mathbb{Z}\)
Vì \(x \in \mathbb{Z}\) suy ra \(\sqrt x \in \mathbb{Z}\) (\(x\) là số chính phương) hoặc \(\sqrt x \in I\) (là số vô tỉ)
TH1: \(\sqrt x \in I\) là số vô tỉ \( \Rightarrow \sqrt x - 3\) là số vô tỉ
\( \Rightarrow \dfrac{8}{{\sqrt x - 3}}\) là số vô tỉ (Loại)
TH2: \(\sqrt x \in \mathbb{Z} \Rightarrow \sqrt x - 3 \in \mathbb{Z}\)
\(\dfrac{8}{{\sqrt x - 3}} \in \mathbb{Z} \Rightarrow 8 \vdots \left( {\sqrt x - 3} \right)\) hay \(\left( {\sqrt x - 3} \right) \in \)Ư\(\left( 8 \right) = \left\{ { \pm 1; \pm 2; \pm 4; \pm 8} \right\}\)
Ta có bảng sau:
|
\(\sqrt x - 3\) |
\( - 8\) |
\( - 4\) |
\( - 2\) |
\( - 1\) |
\(1\) |
\(2\) |
\(4\) |
\(8\) |
|
\(\sqrt x \) |
\( - 5\) |
\( - 1\) |
1 |
2 |
4 |
5 |
7 |
\(11\) |
|
\(x\) |
Loại (vì \(\sqrt x = - 5\)) |
Loại (vì\(\sqrt x = - 1\)) |
\(1\left( {tm} \right)\) |
\(4\left( {tm} \right)\) |
\(16\left( {tm} \right)\) |
\(25\left( {tm} \right)\) |
\(49\left( {tm} \right)\) |
\(121\left( {tm} \right)\) |
Vậy để \(A\)có giá trị nguyên thì \(x \in \left\{ {1;4;16;25;49;121} \right\}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra giữa học kì 1 Toán 7 - Đề số 3 - Kết nối tri thức timdapan.com"







