Đề thi giữa kì 1 Toán 6 - Đề số 13 - Chân trời sáng tạo

Đề bài

Phần trắc nghiệm

Câu 1. Cho tập hợp \(A = \left\{ {2;4;6;8;10} \right\}\). Khẳng định nào sau đâu là sai?

A. \(4 \in A\)

B. \(3 \notin A\)

C. \(7 \in A\)

D. \(1 \notin A\)

Câu 2. Tập hợp các chữ cái Tiếng Việt trong cụm từ "HIỆP HÒA" là:

A. {H; I; Ê; P; H; O; A}

B. {H; I; Ệ; P; H; Ò; A}

C. {H; I; Ệ; P; Ò; A}

D. {H; I; Ê; P; O; A}

Câu 3. Khẳng định nào sau đây là sai?

A. Mọi số tự nhiên đều có số liền trước.

C. Mỗi số tự nhiên có duy nhất một số liền sau.

B. Mọi số tự nhiên đều có số liền sau.

D. Số 0 là số tự nhiên nhỏ nhất.

Câu 4. Biểu diễn phép tính sau về dạng một lũy thừa: \({2^{2023}}:{2^{2022}} \cdot {2^2}\)

A. \({2^2}\)

B. \({2^3}\)

C. 8

D. \({2^{2024}}\)

Câu 5. Trong các tổng sau, tổng nào chia hết cho 3:

A. \(400 + 30\)

B. \(123 + 93\)

C. \(13 + 27\)

D. 2.3.4 +25

Câu 6. Số nào sau đây là bội của 9?

A. 509

B. 3

C. 609

D. 153

Câu 7. Tập hợp các ước của 10 là:

A. Ư\(\left( {10} \right) = \left\{ {1,2,5,10} \right\}\)

B. Ư\(\left( {10} \right) = \left\{ {1;2;5;10} \right\}\)

C. Ư\(\left( {10} \right) = \left\{ {0;1;2;5;10} \right\}\)

D. Ư\(\left( {10} \right) = \left\{ {0;10;20;30; \ldots } \right\}\)

Câu 8. Điền chữ số vào dấu * để số \(\overline {37{\rm{*}}} \) chia hết cho cả 2 và 5:

A. \({\rm{*}} = 2\)

B. \({\rm{*}} = 5\)

C. \({\rm{*}} = 0\) và \({\rm{*}} = 5\)

D. \({\rm{*}} = 0\)

Câu 9. Trong các biển báo giao thông sau, biển báo nào có hình dạng là tam giác đều?

 

A. Biển báo 3.

B. Biển báo 4.

C. Biển báo 1.

D. Biển báo 2.

Câu 10. Mỗi góc của hình lục giác đều bằng

A. \({45^ \circ }\).

B. \({60^ \circ }\).

C. \({90^ \circ }\).

D. \({120^ \circ }\).

Câu 11. Hình bình hành không có tính chất nào dưới đây?

A. Hai cạnh đối bằng nhau.

B. Hai cạnh đối song song với nhau.

C. Hai góc đối bằng nhau.

D. Bốn cạnh bằng nhau.

Câu 12. Một hình thoi có độ dài hai đường chéo là \(6{\rm{\;cm}}\) và \(8{\rm{\;cm}}\). Diện tích của hình thoi đó là

A. \(24{\rm{\;c}}{{\rm{m}}^2}\).

B. \(48{\rm{\;c}}{{\rm{m}}^2}\).

C. \(14{\rm{\;c}}{{\rm{m}}^2}\).

D. \(28{\rm{\;c}}{{\rm{m}}^2}\).

 

Phần tự luận

Bài 1. Thực hiện phép tính (tính hợp lý nếu có thể)

a) \(49.55 + 45.49\)

b) \(120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2.4} \right)} \right]} \right\}\)

Bài 2.

a) Tìm số tự nhiên \(x\) biết: \(12 - 2.x = 8\).

b) Lớp 6A có 24 học sinh nam, 20 học sinh nữ. Cô giáo chia học sinh trong lớp thành các nhóm học tập sao cho học sinh nam trong các nhóm bằng nhau và số học sinh nữ trong các nhóm bằng nhau. Hỏi cô có thể chia nhiều nhất thành bao nhiêu nhóm như vậy?

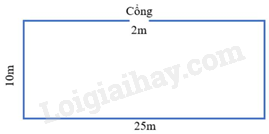
Bài 3. Nhà bác Minh có mảnh vườn hình chữ nhật có chiều dài \(25m\), chiều rộng \(10m\).

a) Hãy tính diện tích mảnh vườn của bác Minh.

b) Bác Minh muốn xây một bức tường bao quanh khu vườn (chỉ để lại cổng vào dài \(2m\)).

Em hãy giúp bác Minh tính chi phí xây dựng bức tường. Biết để xây \(1m\) chiều dài của bức tường cần chi phí 840000 đồng.

 

Bài 4. Chứng tỏ rằng: \({\rm{A}} = 1 + 4 + {4^2} + {4^3} +  \ldots  + {4^{2021}}\) chia hết cho 21.

 

-------- Hết --------

---

Lời giải

Phần trắc nghiệm

 

Câu 1. Cho tập hợp \(A = \left\{ {2;4;6;8;10} \right\}\). Khẳng định nào sau đâu là sai?

A. \(4 \in A\)

B. \(3 \notin A\)

C. \(7 \in A\)

D. \(1 \notin A\)

Phương pháp:

Xác định các phần tử thuộc hay không thuộc tập hợp.

Lời giải:

\(7 \notin A\)

Đáp án C.

Câu 2. Tập hợp các chữ cái Tiếng Việt trong cụm từ "HIỆP HÒA" là:

A. {H; I; Ê; P; H; O; A}

B. {H; I; Ệ; P; H; Ò; A}

C. {H; I; Ệ; P; Ò; A}

D. {H; I; Ê; P; O; A}

Phương pháp:

Liệt kê các chữ cái trong từ “HIỆP HÒA”, chú ý mỗi chữ cái chỉ xuất hiện 1 lần.

Lời giải:

Tập hợp các chữ cái Tiếng Việt trong cụm từ "HIỆP HÒA" là: {H; I; Ê; P; O; A}

Đáp án D.

Câu 3. Khẳng định nào sau đây là sai?

A. Mọi số tự nhiên đều có số liền trước.

C. Mỗi số tự nhiên có duy nhất một số liền sau.

B. Mọi số tự nhiên đều có số liền sau.

D. Số 0 là số tự nhiên nhỏ nhất.

Phương pháp:

Sử dụng tính chất của tập hợp số tự nhiên.

Lời giải:

Số 0 không có số tự nhiên liền trước \( \Rightarrow \) A sai.

Đáp án A.

Câu 4. Biểu diễn phép tính sau về dạng một lũy thừa: \({2^{2023}}:{2^{2022}} \cdot {2^2}\)

A. \({2^2}\)

B. \({2^3}\)

C. 8

D. \({2^{2024}}\)

Phương pháp:

Áp dụng công thức nhân chia hai lũy thừa cùng cơ số. Chú ý viết kết quả dưới dạng lũy thừa.

Lời giải:

\({2^{2023}}:{2^{2022}} \cdot {2^2} = {2^{2023 - 2022 + 2}} = {2^3}\)

Đáp án B.

Câu 5. Trong các tổng sau, tổng nào chia hết cho 3:

A. \(400 + 30\)

B. \(123 + 93\)

C. \(13 + 27\)

D. 2.3.4 +25

Phương pháp:

Áp dụng tính chất chia hết cho một tổng.

Lời giải:

Vì 123 và 93 đều chia hết cho 3 nên \(123 + 93 \vdots 3.\)

Đáp án B.

Câu 6. Số nào sau đây là bội của 9?

A. 509

B. 3

C. 609

D. 153

Phương pháp:

Sử dụng khái niệm bội và ước của một số nguyên:

Nếu \(a,b,x \in \mathbb{N}\) và \(a = b.x\) thì \(a \vdots b\) và a là một bội của b; b là một ước của a.

Lời giải:

Vì \(153 \vdots 9\) nên 153 là bội của 9.

Đáp án D.

Câu 7. Tập hợp các ước của 10 là:

A. Ư\(\left( {10} \right) = \left\{ {1,2,5,10} \right\}\)

B. Ư\(\left( {10} \right) = \left\{ {1;2;5;10} \right\}\)

C. Ư\(\left( {10} \right) = \left\{ {0;1;2;5;10} \right\}\)

D. Ư\(\left( {10} \right) = \left\{ {0;10;20;30; \ldots } \right\}\)

Phương pháp:

Liệt kê các ước của 10 trong dấu ngoặc kép, các phần tử cách nhau bởi dấu “;”.

Lời giải:

Tập hợp các ước của 10 là: Ư\(\left( {10} \right) = \left\{ {1;2;5;10} \right\}\)

Đáp án B.

Câu 8. Điền chữ số vào dấu * để số \(\overline {37{\rm{*}}} \) chia hết cho cả 2 và 5:

A. \({\rm{*}} = 2\)

B. \({\rm{*}} = 5\)

C. \({\rm{*}} = 0\) và \({\rm{*}} = 5\)

D. \({\rm{*}} = 0\)

Phương pháp:

Sử dụng tính chất chia hết cho 2 và 5.

Lời giải:

Vì \(\overline {37{\rm{*}}} \) chia hết cho 2 và 5 nên \({\rm{*}} = 0\)

Đáp án D.

Câu 9. Trong các biển báo giao thông sau, biển báo nào có hình dạng là tam giác đều?

 

A. Biển báo 3.

B. Biển báo 4.

C. Biển báo 1.

D. Biển báo 2.

Phương pháp:

Nhận biết hình tam giác đều.

Lời giải:

Biển báo 1 có dạng hình tam giác đều.

Đáp án C.

Câu 10. Mỗi góc của hình lục giác đều bằng

A. \({45^ \circ }\).

B. \({60^ \circ }\).

C. \({90^ \circ }\).

D. \({120^ \circ }\).

Phương pháp:

Dựa vào đặc điểm của lục giác đều.

Lời giải:

Mỗi góc của hình lục giác đều bằng \({60^ \circ }\).

Đáp án B.

Câu 11. Hình bình hành không có tính chất nào dưới đây?

A. Hai cạnh đối bằng nhau.

B. Hai cạnh đối song song với nhau.

C. Hai góc đối bằng nhau.

D. Bốn cạnh bằng nhau.

Phương pháp:

Dựa vào tính chất của hình bình hành.

Lời giải:

Hình bình hành không có hai góc đối bằng nhau.

Đáp án C.

Câu 12. Một hình thoi có độ dài hai đường chéo là \(6{\rm{\;cm}}\) và \(8{\rm{\;cm}}\). Diện tích của hình thoi đó là

A. \(24{\rm{\;c}}{{\rm{m}}^2}\).

B. \(48{\rm{\;c}}{{\rm{m}}^2}\).

C. \(14{\rm{\;c}}{{\rm{m}}^2}\).

D. \(28{\rm{\;c}}{{\rm{m}}^2}\).

Phương pháp:

Áp dụng công thức tính diện tích hình thoi có độ dài hai đường chéo là m, n.

\(S = m.n:2\)

Lời giải:

Diện tích hình thoi là: \(6.8:2 = 24\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)

Đáp án A.

 

Phần tự luận.

Bài 1. Thực hiện phép tính (tính hợp lý nếu có thể)

a) \(49.55 + 45.49\)

b) \(120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2.4} \right)} \right]} \right\}\)

Phương pháp:

Áp dụng các quy tắc tính cộng, trừ, nhân, chia, lũy thừa.

Lời giải:

 \(\begin{array}{*{20}{c}}{{\rm{a}})\,\,49.55 + 45.49 = 49.(55 + 45)}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 49.100}\\{\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 4900}\end{array}\)

\(\begin{array}{*{20}{c}}\begin{array}{l}{\rm{b)\;}}\,120:\left\{ {54 - \left[ {50:2 - \left( {{3^2} - 2.4} \right)} \right]} \right\}\\ = 120:\{ 54 - [50:2 - (9 - 8)]\} \end{array}\\\begin{array}{l} = 120:\{ 54 - [25 - 1]\} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\ = 120:\{ 54 - 24\} \end{array}\\{ = 120:30 = 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}\)

Bài 2.

a) Tìm số tự nhiên \(x\) biết: \(12 - 2.x = 8\).

b) Lớp 6A có 24 học sinh nam, 20 học sinh nữ. Cô giáo chia học sinh trong lớp thành các nhóm học tập sao cho học sinh nam trong các nhóm bằng nhau và số học sinh nữ trong các nhóm bằng nhau. Hỏi cô có thể chia nhiều nhất thành bao nhiêu nhóm như vậy?

Phương pháp:

Áp dụng các quy tắc thực hiện phép tính.

Lời giải:

\(\begin{array}{l}{\rm{a}})\,12 - 2.x = 8\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2.x = 12 - 8\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,2.x = 4\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 4:2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2\end{array}\)

b) Vì 24 học sinh nam và 20 học sinh nữ chia đều cho các nhóm nên số nhóm có thể chia được nhiều nhất là ước chung lớn nhất của 24 và 20.

Ta có: \(24 = {2^3}.3\); \(20 = {2^2}.5\)

Suy ra ƯCLN\((24,20) = {2^2} = 4\)

Vậy có thể chia nhiều nhất thành 4 nhóm.

Bài 3. Nhà bác Minh có mảnh vườn hình chữ nhật có chiều dài \(25m\), chiều rộng \(10m\).

a) Hãy tính diện tích mảnh vườn của bác Minh.

b) Bác Minh muốn xây một bức tường bao quanh khu vườn (chỉ để lại cổng vào dài \(2m\)).

Em hãy giúp bác Minh tính chi phí xây dựng bức tường. Biết để xây \(1m\) chiều dài của bức tường cần chi phí 840000 đồng.

 

Phương pháp:

- Áp dụng công thức tính chu vi, diện tích hình chữ nhật.

\(\begin{array}{l}C = 2.\left( {a + b} \right)\\S = a.b\end{array}\)

- Tính chiều dài bức tường cần xây = Chu vi hình chữ nhật – Chiều dài lối đi

- Chi phí xây dựng bức tường = Chiều dài bức tường × Giá tiền mỗi mét

Lời giải:                                

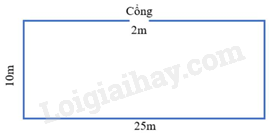
a) Diện tích mảnh vườn là:

\(25.10 = 250\left( {\;{{\rm{m}}^2}} \right)\)

Vậy mảnh vườn có diện tích \(250\;{{\rm{m}}^2}\).

b) Chiều dài bức tường cần xây là: \((10 + 25).2 - 2 = 68(\;{\rm{m}})\)

Chi phí xây dựng bức tường là:\(68.840\,000 = 57\,120\,000\)(đồng)

Vậy chi phí để xây dựng bức tường là 57 120 000 đồng.

Bài 4. Chứng tỏ rằng: \({\rm{A}} = 1 + 4 + {4^2} + {4^3} +  \ldots  + {4^{2021}}\) chia hết cho 21.

Phương pháp:

Chia thành các nhóm, mỗi nhóm gồm 3 số hạng liền nhau.

Lời giải:

Ta có:

\(\begin{array}{l}A = 1 + 4 + {4^2} + {4^3} +  \ldots  + {4^{2021}}\\\,\,\,\,\, = \left( {1 + 4 + {4^2}} \right) + \left( {{4^3} + {4^4} + {4^5}} \right) +  \ldots  + \left( {{4^{2019}} + {4^{2020}} + {4^{2021}}} \right)\\\,\,\,\,\, = \left( {1 + 4 + {4^2}} \right) + {4^3}\left( {1 + 4 + {4^2}} \right) +  \ldots  + {4^{2019}}\left( {1 + 4 + {4^2}} \right)\\\,\,\,\,\, = 21.\left( {1 + {4^3} +  \ldots  + {4^{2019}}} \right)\end{array}\)

Vì \(21 \vdots 21\) nên \(A \vdots 21\).