Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương I - Hình học 12
Đáp án và lời giải chi tiết Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương I - Hình học 12
Đề bài
Câu 1: Cho một hình đa diện. Tìm khẳng định sai trong các khẳng định sau:
A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh
B. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt
C. Mỗi cạnh là cạnh chung của ít nhất ba mặt
D. Mỗi mặt có ít nhất ba cạnh
Câu 2: Một hình lăng trụ có 28 đỉnh sẽ có bao nhiêu cạnh
A. 42 B. 56
C. 48 D. Đáp án khác
Câu 3: Số cạnh của một hình bát diện đều là:
A. Tám B. Mười
C. Mười hai D. Mười sáu
Câu 4: Hai khối chóp lần lượt có diện tích đáy, chiều cao và thể tích là \({B_1},{h_1},{V_1}\) và \({B_2},{h_2},{V_2}\). Biết \({B_1} = {B_2}\) và \({h_1} = 2{h_2}\). Khi đó \(\dfrac{{{V_1}}}{{{V_2}}}\) bằng:
A. 2 B. \(\dfrac{1}{3}\)
C. \(\dfrac{1}{2}\) D. \(\dfrac{1}{6}\)
Câu 5: Khối chóp tam giác có thể tích \(\dfrac{{2{a^3}}}{3}\) và chiều cao \(a\sqrt 3 \) thì diện tích đáy của khối chóp bằng:
A. \(\dfrac{{2\sqrt 3 {a^2}}}{3}\) B. \(2\sqrt 3 {a^2}\)
C. \(\sqrt 3 {a^2}\) D. \(\dfrac{{2\sqrt 3 {a^2}}}{9}\)
Câu 6: Khối hộp chữ nhât. ABCD.A’B’C’D’ có AB = a, AC = 2a và AA’ = 2a. Thể tích khối hộp là:
A. \(2\sqrt 3 {a^3}\) B. \(2{{\rm{a}}^3}\) C. \({a^3}\sqrt 3 \) D. \(4{{\rm{a}}^3}\)
Câu 7. Cho khối chóp \(S.ABC\)có \(SA \bot \left( {ABC} \right),\) tam giác \(ABC\) vuông tại \(B\), \(AB = a,\,AC = a\sqrt 3 .\) Tính thể tích khối chóp \(S.ABC\) biết rằng \(SB = a\sqrt 5 \)
A. \(\dfrac{{{a^3}\sqrt 6 }}{4}\) B. \(\dfrac{{{a^3}\sqrt 2 }}{3}\)
C. \(\dfrac{{{a^3}\sqrt 6 }}{6}\) D. \(\dfrac{{{a^3}\sqrt {15} }}{6}\)
Câu 8. Cho hình chóp SA BC có đáy ABC là tam giác vuông cân tại B với AC = a biết SA vuông góc với đáy ABC và SB hợp với đáy một góc 60o. Tính thể tích hình chóp
A. \(\dfrac{{{a^3}\sqrt 6 }}{{24}}\) B. \(\dfrac{{{a^3}\sqrt 3 }}{{24}}\)
C. \(\dfrac{{{a^3}\sqrt 6 }}{8}\) D. \(\dfrac{{{a^3}\sqrt 6 }}{{48}}\)
Câu 9. Cho khối chóp \(S.ABCD\)có đáy là hình vuông cạnh \(2a\). Gọi \(H\) là trung điểm cạnh \(AB\) biết \(SH \bot \left( {ABCD} \right)\) . Tính thể tích khối chóp biết tam giác \(SAB\) đều
A. \(\dfrac{{2{a^3}\sqrt 3 }}{3}\) B. \(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
C. \(\dfrac{{{a^3}}}{6}\) D. \(\dfrac{{{a^3}}}{3}\)
Câu 10. Cho hình chóp SABC có đáy ABC vuông cân tại a với AB = AC = a biết tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với (ABC) ,mặt phẳng (SAC) hợp với (ABC) một góc 45o. Tính thể tích của SABC.
A. \(\dfrac{{{a^3}}}{{12}}\) B. \(\dfrac{{{a^3}}}{6}\)
C. \(\dfrac{{{a^3}}}{{24}}\) D. \({a^3}\)
Câu 11: Hình chóp đều S.ABCD có cạnh đáy bằng \(2a\) và cạnh bên bằng \(3a\). Thể tích hình chóp S.ABCD ?
A. \(4\sqrt 7 {a^3}\) B. \(\dfrac{{\sqrt 7 }}{3}{a^3}\)
C. \(\dfrac{4}{3}{a^3}\) D. \(\dfrac{{4\sqrt 7 }}{3}{a^3}\)
Câu 12: Hình chóp đều S.ABC có cạnh đáy bằng \(a\) và cạnh bên tạo với đáy một góc bằng \({30^0}\). Thể tích của hình chóp S.ABC là ?
A. \(\dfrac{{\sqrt 2 }}{{12}}{a^3}\) B. \(\dfrac{{\sqrt 3 }}{{36}}{a^3}\)
C. \(\dfrac{{\sqrt 3 }}{{12}}{a^3}\) D. \(\dfrac{{\sqrt 6 }}{{36}}{a^3}\)
Câu 13. Xét hình chóp S.ABC với M, N, P lần lượt là các điểm trên SA, SB, SC sao cho \(\dfrac{{SM}}{{MA}} = \dfrac{{SN}}{{NB}} = \dfrac{{SP}}{{PC}} = \dfrac{1}{2}\). Tỉ số thể tích của khối tứ diện SMNP với SABC là:
A. \(\dfrac{1}{9}\). B. \(\dfrac{1}{{27}}\).
C. \(\dfrac{1}{4}\). D. \(\dfrac{1}{8}\).
Câu 14: Cho khối lăng trụ đứng ABC.A’B’C’,đáy ABC là tam giác vuông tại B,AB=BC=2a,AA’=\(a\sqrt 3 \).Tính thể tích khối lăng trụ ABC.A’B’C’.
A.\(2{a^3}\sqrt 3 \) B.\(\dfrac{{2{a^3}\sqrt 3 }}{3}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{3}\) D.\({a^3}\sqrt 3 \)
Câu 15: Nếu ba kích thước của một khối chữ nhật tăng lên 4 lần thì thể tích của nó tăng lên:
A. 4 lần B. 16 lần
C. 64 lần D. 192 lần
Câu 16. Thể tích \(V\) của khối lập phương \(ABCD.A'B'C'D'\), biết \(AB = 3a\) là:
A. \(6{a^3}\) . B. \(9{a^3}\) .
C. \(\dfrac{{{a^3}}}{3}\) D. \(27{a^3}\)
Câu 17: Cho hình hộp ABCD.A’B’C’D’ có đáy ABCD là hình thoi cạnh a,\(\widehat {BCD} = {120^0}\) và \(AA' = \dfrac{{7a}}{2}\). Hình chiếu vuông góc của A’ lên mặt phẳng (ABCD) trùng với giao điểm của AC và BD. Tính theo a thể tích khối hộp ABCD.A’B’C’D’.
A. \(V = 12{a^3}\) B. \(V = 3{a^3}\)
C. \(V = 9{a^3}\) D. \(V = 6{a^3}\)
Câu 18: thể tích của khối hộp chữ nhật ABCDA’B’C’D’ có AB = a; BC = b; AA’ = c là:
A. \(V = a^3\) B. \(V = b^3\)
C. \(V = c^3\) D. \(V = abc\)
Câu 19: số mặt phẳng đối xứng của hình chóp tứ giác đều:
A. 3 B. 4
C. 5 D. 6.
Câu 20: Hình nào trong các hình sau không phải là hình đa diện?
A. Hình lăng trụ
B. Hình vuông
C. Hình hộp
D. Hình chóp
Lời giải chi tiết
|
Câu |
1 |
2 |
3 |
4 |
5 |
|
Đáp án |
C |
A |
C |
A |
A |
|
Câu |
6 |
7 |
8 |
9 |
10 |
|
Đáp án |
A |
B |
A |
B |
A |
|
Câu |
11 |
12 |
13 |
14 |
15 |
|
Đáp án |
D |
B |
B |
A |
C |
|
Câu |
16 |
17 |
18 |
19 |
20 |
|
Đáp án |
D |
B |
D |
B |
B |
Câu 1
Chọn đáp án C
Câu 2
Chọn đáp án A.
Câu 3
Chọn đáp án C.
Câu 4
Ta có: \({V_1} = \dfrac{1}{3}{B_1}{h_1} = \dfrac{2}{3}{B_2}{h_2}\)
\({V_2} = \dfrac{1}{3}{B_2}{h_2} \Rightarrow \dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{2}{3}{B_2}{h_2}}}{{\dfrac{1}{3}{B_2}{h_2}}} = 2\)
Chọn đáp án A.
Câu 5
Ta có: \(V = \dfrac{1}{3}S.h \)
\(\Rightarrow \dfrac{{2{a^3}}}{3} = \dfrac{1}{3}.a\sqrt 3 .S \)
\(\Rightarrow S = \dfrac{{2{a^2}\sqrt 3 }}{3}\)
Chọn đáp án A.
Câu 6
\(BC = \sqrt {\left( {2{a^2}} \right) - {a^2}} = a\sqrt 3 \)
Ta có: \({V_{ABCD.A'B'C'D'}} = AB.BC.{\rm{AA'}}\;\)\({\rm{ = }}\;a.a\sqrt 3.2a\;\)\({\rm{ = }}\;2\sqrt 3 {a^3}\)
Chọn đáp án A.
Câu 7
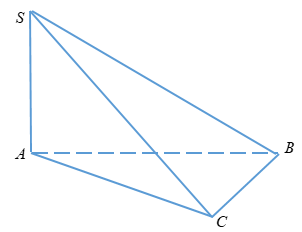
Ta có tam giác ABC vuông tại B
Áp dụng định lý Py – ta – go ta có:
\(BC = \sqrt {A{C^2} - A{B^2}} = \sqrt {3{a^2} - {a^2}} = a\sqrt 2 \)
+ \(SA = \sqrt {S{B^2} - A{B^2}} = \sqrt {5{a^2} - {a^2}} = 2a\)
Khi đó ta có:
\({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.2a.\dfrac{1}{2}.a\sqrt 2 .a \)\(\,= \dfrac{{{a^3}\sqrt 2 }}{3}\)
Chọn đáp án B
Câu 8
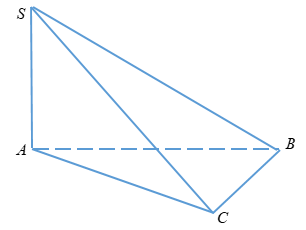
Tam giác ABC vuông cân tại B
Ta có:
\(A{B^2} + B{C^2} = A{C^2} \)
\(\Rightarrow AB = \sqrt {\dfrac{{A{C^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\)
\(\tan {60^ \circ } = \dfrac{{SA}}{{AB}} \)
\(\Rightarrow SA = \tan {60^ \circ }.AB = \sqrt 3 .\dfrac{{a\sqrt 2 }}{2} = \dfrac{{a\sqrt 6 }}{2}\)
Khi đó ta có:
\(V = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt 6 }}{2}.\dfrac{1}{2}{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^2}\)\(\, = \dfrac{{{a^3}\sqrt 6 }}{{24}}\)
Chọn đáp án A.
Câu 9
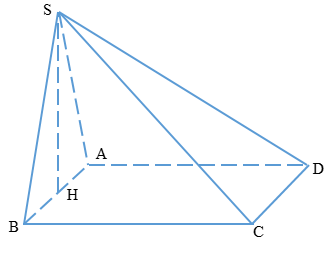
Tam giác SAB đều
\( \Rightarrow SA = SB = AB = 2a\)
+ \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \)
Khi đó ta có:
\({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}} = \dfrac{1}{3}a\sqrt 3 .4{a^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}\)
Chọn đáp án B
Câu 10
Tam giác SAB nằm trong mặt phẳng vuông góc với đáy.
Gọi H là trung điểm của AB
\( \Rightarrow SH \bot AB\) hay \(SH \bot \left( {ABC} \right)\)
+ Mặt phẳng (SAC) hợp với (ABC) một góc 45o
\( \Rightarrow \dfrac{{SH}}{{AH}} = \tan {45^ \circ } \Leftrightarrow SA = AH = \dfrac{a}{2}\)
Khi đó \(V = \dfrac{1}{3}SH.S{}_{ABC} = \dfrac{1}{3}.\dfrac{a}{2}.\dfrac{1}{2}a.a = \dfrac{{{a^3}}}{{12}}\)
Chọn đáp án A.
Câu 11
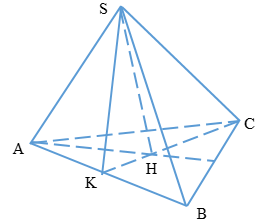
Chiều cao của hình chóp \(h = \sqrt {9{a^2} - 2a{}^2} = a\sqrt 7 \)
Thể tích hình chóp:\(V = \dfrac{1}{3}.h.S = \dfrac{1}{3}.a\sqrt 7 .4{a^2} = \dfrac{{4{a^3}\sqrt 7 }}{3}\)
Chọn đáp án D.
Câu 12
Tam giác ABC đều, gọi H là giao điểm của các đường cao.
+ Cạnh bên tạo với đáy một góc bằng \({30^0}\)
\( \Rightarrow \tan {30^0} = \dfrac{{SH}}{{AH}}\)
Mà \(AH = \dfrac{2}{3}\sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\)
\( \Rightarrow SH = AH.\tan {30^0} = \dfrac{{a\sqrt 3 }}{3}.\dfrac{{\sqrt 3 }}{3} = \dfrac{a}{3}\)
Vậy \(V = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{1}{2}.a.a.\sin {60^0} = \dfrac{{\sqrt 3 }}{{36}}{a^3}\)
Chọn đáp án B.
Câu 13
Ta có: \(\dfrac{{SM}}{{MA}} = \dfrac{{SN}}{{NB}} = \dfrac{{SP}}{{PC}} = \dfrac{1}{2} \)
\(\Rightarrow \dfrac{{SM}}{{SA}} = \dfrac{{SN}}{{SB}} = \dfrac{{SP}}{{SC}} = \dfrac{1}{3}\)
Khi đó \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}} = {\left( {\dfrac{1}{3}} \right)^3} = \dfrac{1}{{27}}\)
Chọn đáp án B.
Câu 14
Thể tích khối lăng trụ \(V = \dfrac{1}{2}2a.2a.\sqrt 3 = 2{a^3}\sqrt 3 \)
Chọn đáp án A.
Câu 15
Thể tích hình khố chữ nhật ban đầu: \(V = abc\)
Thể tích khối mới : \({V_m} = 4a.4b.4c = 64abc\)
Chọn đáp án C.
Câu 16
Thể tích của khối lập phương là \(V = {\left( {3a} \right)^3} = 27{a^3}\)
Chọn đáp án D.
Câu 17
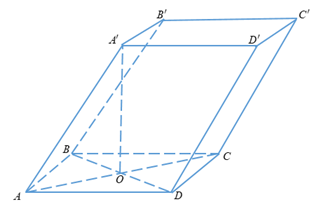
Ta có: \(\widehat {BCD} = \widehat {BAD} = {120^0}\)
\( \Rightarrow \widehat {ABC} = \widehat {ADC} = {60^0}\)
\( \Rightarrow AB = BC = AC = a\)
Áp dụng định lý Py – ta – go ta có:
\(OA' = \sqrt {A{{A'}^2} - O{A^2}} \)\(\,= \sqrt {\dfrac{{49{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = 2a\sqrt 3 \)
Khi đó ta có:
\({V_{ABCD.A'B'C'D'}} = A'O.{S_{ABCD}} \)\(\,= 2a\sqrt 3 .a.a.\sin 60 = 3{a^3}\)
Chọn đáp án B.
Câu 18
Thể tích khối hộp chữ nhật là \(V = abc\)
Chọn đáp án D.
Câu 19
Chọn đáp án B
Câu 20
Hình vuông không phải là hình đa diện.
Chọn đáp án B.
Loigiaihaycom
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương I - Hình học 12 timdapan.com"







