Đề kiểm tra 45 phút ( 1 tiết) - Đề số 1 - Chương 1 - Hình học 11

Đề bài

Câu 1. Trong mặt phẳng Oxy, tìm ảnh của đường tròn \(\left( C \right):{\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 5\) qua phép quay \({Q_{\left( {O,{{180}^0}} \right)}}\)

A. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 10\)

B. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 5\)

C. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 5} \right)^2} = 5\)

D. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y + 5} \right)^2} = 5\)

Câu 2. Trong mp Oxy cho (C): \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 9\). Phép tịnh tiến theo \(\vec v\left( {3; - 2} \right)\) biến (C) thành đường tròn nào?

A. \({\left( {x - 6} \right)^2} + {\left( {y - 9} \right)^2} = 9\)

B. \({x^2} + {y^2} = 9\)

C. \({\left( {x - 6} \right)^2} + {\left( {y + 4} \right)^2} = 9\)

D. \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} = 9\)

Câu 3. Giả sử phép dời hình \(f\) biến tam giác \(ABC\) thành tam giác A’B’C’. Xét các mệnh đề sau:

(I): Trọng tâm tam giác ABC biến thành trọng tâm tam giác A’B’C’

(II): Trực tâm tam giác ABC biến thành trực tâm tam giác A’B’C’

(III): Tâm đường tròn ngoại tiếp, nội tiếp tam giác ABC lần lượt biến thành tâm đường tròn ngoại tiếp, nội tiếp tam giác A’B’C’.

Số mệnh đề đúng trong 3 mệnh đề trên là:

A. 3                             B. 1

C. 2                             D. 0

Câu 4. Cho \(\Delta ABC\) có trọng tâm \(G\). Gọi \(M,N,P\) lần lượt là trung điểm của các cạnh \(AB,BC,CA\). Phép vị tự nào sau đây biến \(\Delta ABC\) thành \(\Delta NPM\)?

A. \({V_{\left( {M,\frac{1}{2}} \right)}}\).   B. \({V_{\left( {A, - \frac{1}{2}} \right)}}\).

C. \({V_{\left( {G, - \frac{1}{2}} \right)}}\). D. \({V_{\left( {G, - 2} \right)}}\).

Câu 5. Trong mặt phẳng Oxy cho đường tròn \(\left( C \right):{x^2} + {y^2} = 4\) và đường thẳng \(d:x - y + 2 = 0\). Gọi M là điểm thuộc đường tròn (C) sao cho khoảng cách đến d là lớn nhất. Phép vị tự tâm O tỉ số \(k = \sqrt 2 \) biến điểm M thành điểm \(M'\) có tọa độ là?

A. \(\left( { - 2\,;\,2} \right)\)                          B. \(\left( {2\,;\,2} \right)\)

C. \(\left( { - 2\,;\,2} \right)\)                           D. \(\left( {2\,;\, - 2} \right)\)

Câu 6. Cho lục giác đều ABCDEF tâm O. Ảnh của tam giác COD qua phép tịnh tiến theo véctơ \(\overrightarrow {BA} \) là:

A. \(\Delta OFE\)         B. \(\Delta COB\)

C. \(\Delta DOE\)         D. \(\Delta ODC\)

Câu 7. Trong mặt phẳng với hệ trục tọa độ Oxy, cho 2 đường tròn (C) và (C’) có phương trình lần lượt là: \({x^2} + {\left( {y - 2} \right)^2} = 4\) và \({x^2} + {y^2} - 2x + 2y = 23\). Gọi (C’) là ảnh của (C) qua phép đồng dạng tỉ số k, khi đó giá trị k là:

A. \(\frac{5}{2}\)        B. \(\frac{{23}}{4}\)

C. \(\frac{4}{{23}}\)   D. \(\frac{2}{5}\)

Câu 8. Trong mặt phẳng \(Oxy\) cho đường tròn \(\left( C \right)\) ngoại tiếp tam giác ABC, với \(A\left( {3;4} \right),B\left( { - 3; - 2} \right),C\left( {9; - 2} \right)\). Tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow v  = \left( {3;5} \right)\) và phép vị tự \({V_{\left( {O; - \frac{1}{3}} \right)}}.\)

A. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 2.\)

B. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 4.\)

C. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 6.\)

D. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 36.\)

Câu 9. Chọn khẳng định sai trong các khẳng định sau:

A. Phép tịnh tiến biến một đường tròn thành một đường tròn có cùng bán kính.

B. Phép tịnh tiến luôn biến một đường thẳng thành một đường thẳng song song với nó.

C. Phép quay bảo toàn khoảng cách giữa hai điểm bất kì.

D. Phép tịnh tiến biến ba điểm thẳng hàng thành ba điểm thẳng hàng.

Câu 10. Cho lục giác đều ABCDEF như hình vẽ.

Phép quay tâm O góc \({120^0}\)biến tam giác AOE thành tam giác nào?

A. Tam giác EOC

B. Tam giác AOB.

C. Tam giác DOC.

D. Tam giác DOE.

Câu 11. Tính chất nào sau đây không phải là tính chất của phép dời hình?

A. Biến đoạn thẳng thành đoạn thẳng có độ dài gấp k lần đoạn thẳng ban đầu \(\left( {k \ne 1} \right)\).

B. Biến đường tròn thành đường tròn bằng nó.

C. Biến tam giác thành tam giác bằng nó, biến tia thành tia.

D. Biến ba điểm thẳng hàng thành ba điểm thẳng hàng bảo toàn thứ tự của ba điểm đó.

Câu 12. Trong mặt phẳng tọa độ Oxy cho đường thẳng \(d:x - 2y - 5 = 0.\) Ảnh của đường thẳng \(d:x - 2y - 5 = 0\) qua phép quay tâm O góc \(\frac{\pi }{2}\) có phương trình:

A. \(2x + y - 5 = 0.\)

B. \(2x + y + 3 = 0.\)

C. \(2x + 3y - 6 = 0.\)

D. \(x - 2y + 4 = 0.\)

Câu 13. Trong mặt phẳng với hệ tọa độ \(Oxy\), cho đường tròn \(\left( C \right):{x^2} + {\left( {y + 2} \right)^2} = 36\). Khi đó phép vị tự tỉ số \(k = 3\) biến đường tròn \(\left( C \right)\) thành đường tròn \(\left( {C'} \right)\) có bán kính là:

A. \(108\).                    B. \(6\).

C. \(18\).                      D. \(12\).

Câu 14. Cho hai đường thẳng song song \({d_1}:2x - y + 6 = 0;\)\({d_2}:2x - y + 4 = 0\). Phép tịnh tiến theo vectơ \(\overrightarrow u \left( {a;\,b} \right)\) biến đường thẳng \({d_1}\) thành đường thẳng \({d_2}\). Tính \(2a - b\)

A. 4                      B. -4

C. 2                      D. -2

Câu 15. Cho tam giác ABC vuông tại A có đường cao AH, biết AB = 3; AC = 4. Phép dời hình biến A thành A’, biến H thành H’. Khi đó độ dài đoạn A’H’ bằng:

A. 8                             B. 4

C. \(\frac{{12}}{5}\)                              D. 6

Câu 16. Phép biến hình nào dưới đây không phải là phép dời hình?

A. Phép tịnh tiến

B. Phép quay.

C. Phép đồng nhất.

D. Phép vị tự tỉ số \(k{\rm{ }}\left( {k \ne  \pm 1} \right)\).

Câu 17. Trong mặt phẳng tọa độ \(Oxy\), cho hai đường thẳng \(d:x + 3y - 4 = 0\) và \(d':x + 3y - 11 = 0\). Biết rằng phép tịnh tiến theo vectơ \(\overrightarrow v \) biến \(d\) thành \(d'\). Phương án nào dưới đây đúng?

A. \(\overrightarrow v  = (1; - 2)\).           B. \(\overrightarrow v  = ( - 1;2)\).

C. \(\overrightarrow v  = ( - 1; - 2)\).      D. \(\overrightarrow v  = (1;2)\).

Câu 18. Phép vị tự \({V_{(O;k)}}\) biến M thành M’. Khẳng định nào sau đây là đúng?

A. Nếu \(k < 0\) thì \(\overrightarrow {MO} \) và \(\overrightarrow {MM'} \) cùng hướng

B. Nếu k = - 1 thì \(M \equiv M'\)

C. Nếu k = 1 thì M và M’đối xứng nhau qua O

D. Nếu k = 2 thì M’ là trung điểm của OM

Câu 19. Trong mặt phẳng \(Oxy\), cho điểm \(A\left( {3; - 5} \right)\). Tìm tọa độ ảnh \(A'\) của điểm \(A\) qua phép quay \({Q_{\left( {O;\frac{\pi }{2}} \right)}}\).

A. \(A'\left( {3; - 5} \right)\).           B. \(A'\left( {5;3} \right)\).

C. \(A'\left( { - 5;3} \right)\).           D. \(A'\left( { - 3; - 5} \right)\).

Câu 20. Cho \(\Delta ABC\) đều cạnh 2. Qua ba phép đồng dạng liên tiếp: Phép tịnh tiến \({T_{\overrightarrow {BC} }}\), phép quay \(Q\left( {B,\,{{60}^o}} \right)\), phép vị tự \({V_{\left( {A,\,3} \right)}}\), \(\Delta ABC\) biến thành \(\Delta {A_1}{B_1}{C_1}\). Diện tích \(\Delta {A_1}{B_1}{C_1}\) là:

A. \(9\sqrt 2 \)              B. \(5\sqrt 2 \)

C. \(9\sqrt 3 \)              D. \(5\sqrt 3 \)

Câu 21. Cho hình chữ nhật tâm \(O\) (không phải là hình vuông). Hỏi có bao nhiêu phép quay tâm \(O\) góc \(\alpha \) với \(0 \le \alpha  < 2\pi \), biến hình chữ nhật trên thành chính nó?

A. \(4\).                       B. \(2\).

C. \(3\).                        D. \(0\).

Câu 22. Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(M\left( {4;6} \right)\) và \(M'\left( { - 3;5} \right)\). Phép vị tự tâm \(I\), tỉ số \(k =  - \frac{1}{2}\) biến điểm \(M\) thành \(M'\). Tìm tọa độ tâm vị tự \(I\).

A. \(I\left( {11;1} \right)\).              B. \(I\left( {1;11} \right)\).

C. \(I\left( { - 4;10} \right)\).           D. \(I\left( { - \frac{2}{3};\frac{{16}}{3}} \right)\).

Câu 23. Trong mặt phẳng tọa độ \(Oxy\), cho \(\vec v = \left( {2; - 1} \right)\). Tìm ảnh A' của \(A\left( { - 1;2} \right)\) qua phép tịnh tiến theo vectơ \(\vec v\).

A. \(A'\left( {\frac{1}{2};\frac{1}{2}} \right)\).             B. \(A'\left( { - 3;3} \right)\).

C. \(A'\left( {1;1} \right)\).             D. \(A'\left( {3; - 3} \right)\).

Câu 24. Cho tam giác ABC đều, điểm M nằm trong tam giác ABC thỏa mãn \(M{A^2} + M{B^2} = M{C^2}\), nhận xét nào sau đây đúng

A. Góc AMB bằng 150⁰.

B. M, A, B thẳng hàng

C. Không tìm được điểm M thỏa mãn

D. Góc AMB bằng 30⁰

Câu 25. Trong mặt phẳng tọa độ \(Oxy,\) cho \(A\left( {1;2} \right)\). Tìm ảnh \(A'\) của \(A\) qua phép vị tự tâm \(I\left( {3; - 1} \right)\) tỉ số \(k = 2.\)

A. \(A'\left( {1;5} \right)\).         B. \(A'\left( { - 1;5} \right)\).

C. \(A'\left( {3;4} \right)\).        D. \(A'\left( { - 5; - 1} \right)\).

Lời giải chi tiết

ĐÁP ÁN

 

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu 1:

Phương pháp:

Phép quay biến đường tròn thành đường tròn có cùng bán kính.

- Tìm ảnh của tâm đường tròn đã chp qua phép quay và suy ra phương trình.

- Chú ý \({Q_{\left( {O;{{180}^0}} \right)}}\) là phép đối xứng tâm \(O\).

Hướng dẫn giải:

\(\left( C \right)\) có tâm \(I\left( {2; - 5} \right)\) bán kính \(R = \sqrt 5 \).

Gọi \(I' = {Q_{\left( {O;{{180}^0}} \right)}}\left( I \right)\) thì \(I'\) đối xứng với \(I\) qua \(O\)

\( \Rightarrow \left\{ \begin{array}{l}{x_{I'}} =  - {x_I} =  - 2\\{y_{I'}} =  - {y_I} = 5\end{array} \right. \Rightarrow I'\left( { - 2;5} \right)\)

Vậy \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 5\)

Đáp án B

Câu 2:

Phương pháp:

Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

Tìm ảnh của tâm đường tròn qua phép tính tiến và suy ra phương trình.

Hướng dẫn giải:

\(\left( C \right)\) có tâm \(I\left( {3; - 2} \right)\) và bán kính \(R = 3\).

\(\begin{array}{l}I' = {T_{\overrightarrow v }}\left( I \right) \Rightarrow \overrightarrow {II'}  = \overrightarrow v \\ \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = {x_I} + 3 = 3 + 3 = 6\\{y_{I'}} = {y_I} - 2 =  - 2 - 2 =  - 4\end{array} \right.\\ \Rightarrow I'\left( {6; - 4} \right)\end{array}\)

Vậy \(\left( {C'} \right):{\left( {x - 6} \right)^2} + {\left( {y + 4} \right)^2} = 9\)

Đáp án C

Câu 3:

Phương pháp:

Phép dời hình biến tam giác thành tam giác bằng nó.

Hướng dẫn giải:

Sử dụng chú ý a trang 21 SGK hình học 11:

Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm các đường tròn nội tiếp, ngoại tiếp của tam giác A’B’C’.

Vậy cả 3 mệnh đề đều đúng.

Đáp án A

Câu 4:

Hướng dẫn giải:

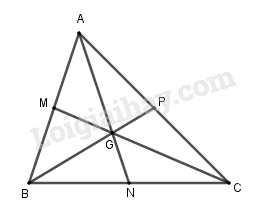
Gọi G là trọng tâm tam giác ABC. Khi đó

\(\overrightarrow {GN}  =  - \frac{1}{2}\overrightarrow {GA} \) \( \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( A \right) = N\)

\(\overrightarrow {GP}  =  - \frac{1}{2}\overrightarrow {GB} \) \( \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( B \right) = P\)

\(\overrightarrow {GM}  =  - \frac{1}{2}\overrightarrow {GC} \) \( \Rightarrow {V_{\left( {G, - \frac{1}{2}} \right)}}\left( C \right) = M\)

Vậy \({V_{\left( {G, - \frac{1}{2}} \right)}}\left( {\Delta ABC} \right) = \Delta NPM\)

Đáp án C

Câu 5:

Phương pháp:

- Viết phương trình đường thẳng d’ đi qua tâm I và vuông góc với d.

- Một trong hai giao điểm của d’ với (C) chính là M.

- Từ đó tìm tọa độ M’.

Hướng dẫn giải:

(C ) có tâm O(0;0) bán kính R=2.

Gọi d’ là đường thẳng đi qua O và vuông góc với d.

 \(\overrightarrow {{n_d}}  = \left( {1; - 1} \right)\) là VTPT của d nên \(\overrightarrow {{n_{d'}}}  = \left( {1;1} \right)\) là VTPT của d’.

Do đó \(d':x + y = 0\).

M là giao điểm của d’ và (C) nên tọa độ của M thỏa mãn hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}x + y = 0\\{x^2} + {y^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - x\\{x^2} + {x^2} = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y =  - x\\2{x^2} = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y =  - x\\{x^2} = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y =  - x\\x =  \pm \sqrt 2 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 ,y =  - \sqrt 2 \\x =  - \sqrt 2 ,y = \sqrt 2 \end{array} \right.\end{array}\)

Xét \({M_1}\left( {\sqrt 2 ; - \sqrt 2 } \right)\) có \(d\left( {{M_1};d} \right) = \frac{{\left| {\sqrt 2  + \sqrt 2  + 2} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = 2 + \sqrt 2 \)

Xét \({M_2}\left( { - \sqrt 2 ;\sqrt 2 } \right)\) có \(d\left( {{M_2};d} \right) = \frac{{\left| { - \sqrt 2  - \sqrt 2  + 2} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }} = 2 - \sqrt 2 \)

Vì \(d\left( {{M_1};d} \right) > d\left( {{M_2};d} \right)\) nên \(M \equiv {M_1}\left( {\sqrt 2 ; - \sqrt 2 } \right)\).

\({V_{\left( {O;\sqrt 2 } \right)}}\left( M \right) = M'\) \( \Rightarrow \left\{ \begin{array}{l}{x_{M'}} = \sqrt 2 {x_M} = \sqrt 2 .\sqrt 2  = 2\\{y_{M'}} = \sqrt 2 {y_M} = \sqrt 2 .\left( { - \sqrt 2 } \right) =  - 2\end{array} \right.\).

Đáp án D

Câu 6:

Hướng dẫn giải:

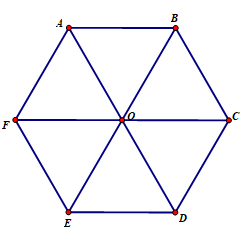
\(\begin{array}{l}\overrightarrow {CO}  = \overrightarrow {BA}  \Rightarrow {T_{\overrightarrow {BA} }}\left( C \right) = O\\\overrightarrow {OF}  = \overrightarrow {BA}  \Rightarrow {T_{\overrightarrow {BA} }}\left( O \right) = F\\\overrightarrow {DE}  = \overrightarrow {BA}  \Rightarrow {T_{\overrightarrow {BA} }}\left( D \right) = E\\ \Rightarrow {T_{\overrightarrow {BA} }}\left( {\Delta COD} \right) = \Delta OFE\end{array}\)

Đáp án A

Câu 7:

Phương pháp:

Phép đồng dạng tỉ số k biến đường tròn bán kính R thành đường tròn có bán kính kR.

Hướng dẫn giải:

\(\left( C \right)\) có bán kính \(R = 2\).

\(\left( {C'} \right)\) có bán kính \(R' = \sqrt {{1^2} + {{\left( { - 1} \right)}^2} - \left( { - 23} \right)}  = 5\).

Vậy tỉ số đồng dạng là \(k = \frac{{R'}}{R} = \frac{5}{2}\).

Đáp án A

Câu 8:

Phương pháp:

- Viết phương trình đường tròn đi qua ba điểm \(A,B,C\).

- Tìm tâm, bán kính và ảnh của tâm đó qua phép đồng dạng đã cho.

- Viết phương trình đường tròn mới.

Hướng dẫn giải:

Gọi phương trình \(\left( C \right)\) là \({x^2} + {y^2} - 2ax - 2by + c = 0\)

\(A,B,C \in \left( C \right)\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{3^2} + {4^2} - 6a - 8b + c = 0\\{\left( { - 3} \right)^2} + {\left( { - 2} \right)^2} + 6a + 4b + c = 0\\{9^2} + {\left( { - 2} \right)^2} - 18a + 4b + c = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 6x - 8b + c =  - 25\\6a + 4b + c =  - 13\\ - 18a + 4b + c =  - 85\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b =  - 2\\c =  - 23\end{array} \right.\\ \Rightarrow \left( C \right):{x^2} + {y^2} - 6x + 4y - 23 = 0\end{array}\)

(C ) có tâm \(I\left( {3; - 2} \right)\) bán kính \(R = \sqrt {{3^2} + {{\left( { - 2} \right)}^2} - \left( { - 23} \right)}  = 6\)

Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\) \( \Rightarrow \left\{ \begin{array}{l}{x_{I'}} = 3 + 3 = 6\\{y_{I'}} =  - 2 + 5 = 3\end{array} \right. \Rightarrow I'\left( {6;3} \right)\)

\(I'' = {V_{\left( {O; - \frac{1}{3}} \right)}}\left( {I'} \right)\) \( \Rightarrow \left\{ \begin{array}{l}{x_{I''}} =  - \frac{1}{3}{x_{I'}} =  - \frac{1}{3}.6 =  - 2\\{y_{I''}} =  - \frac{1}{3}{y_{I'}} =  - \frac{1}{3}.3 =  - 1\end{array} \right.\) \( \Rightarrow I''\left( { - 2; - 1} \right)\)

(C’) có tâm \(I''\left( { - 2; - 1} \right)\) bán kính \(R'' = \left| { - \frac{1}{3}} \right|R = \frac{1}{3}.6 = 2\) nên có phương trình: \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 4.\)

Đáp án B

Câu 9:

Hướng dẫn giải:

Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên B sai.

Đáp án B

Câu 10:

Hướng dẫn giải:

\(\begin{array}{l}{Q_{\left( {O;{{120}^0}} \right)}}\left( A \right) = E\\{Q_{\left( {O;{{120}^0}} \right)}}\left( O \right) = O\\{Q_{\left( {O;{{120}^0}} \right)}}\left( E \right) = C\\ \Rightarrow {Q_{\left( {O;{{120}^0}} \right)}}\left( {\Delta AOE} \right) = \Delta EOC\end{array}\)

Đáp án A

Câu 11:

Hướng dẫn giải:

Phép dời hình biến đoạn thẳng thành đoạn thẳng bằng nó nên A sai.

Đáp án A

Câu 12:

Phương pháp:

- Lấy một điểm A bất kì thuộc d, tìm ảnh của A qua \({Q_{\left( {O;\frac{\pi }{2}} \right)}}\)

- Viết phương trình d’, chú ý \(d' \bot d\).

Hướng dẫn giải:

Lấy \(A\left( {5;0} \right) \in d\), gọi \(A' = {Q_{\left( {O,\frac{\pi }{2}} \right)}}\left( A \right)\) thì \(A'\left( {0;5} \right)\).

Ta có: \(\overrightarrow {{n_d}}  = \left( {1; - 2} \right)\), mà \(d' \bot d\)\( \Rightarrow \overrightarrow {{n_{d'}}}  = \left( {2;1} \right)\).

Vậy \(d':2\left( {x - 0} \right) + 1\left( {y - 5} \right) = 0\) \( \Leftrightarrow 2x + y - 5 = 0\)

Đáp án A

Câu 13:

Hướng dẫn giải:

(C ) có bán kính \(R = 6\) nên (C’) có bán kính \(R' = kR = 3.6 = 18\)

Đáp án C

Câu 14:

Phương pháp:

Lấy điểm M(x;y) bất kì thuộc \({d_1}\).

Tìm ảnh M’ của M qua \({T_{\overrightarrow v }}\) và thay vào \({d_2}\).

Từ đó suy ra \(a;b\).

Hướng dẫn giải:

Lấy M(x;y)\( \in {d_1}\) thì \(2x - y + 6 = 0\)

\(M' = {T_{\overrightarrow v }}\left( M \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = x + a\\{y_{M'}} = y + b\end{array} \right.\) \( \Rightarrow M'\left( {x + a;y + b} \right)\)

\(M' \in {d_2}\) \( \Leftrightarrow 2\left( {x + a} \right) - \left( {y + b} \right) + 4 = 0\)

\(\begin{array}{l} \Leftrightarrow 2x + 2a - y - b + 4 = 0\\ \Leftrightarrow \left( {2x - y + 6} \right) + \left( {2a - b - 2} \right) = 0\\ \Leftrightarrow 0 + \left( {2a - b - 2} \right) = 0\\ \Leftrightarrow 2a - b - 2 = 0\\ \Leftrightarrow 2a - b = 2\end{array}\)

Đáp án C

Câu 15:

Phương pháp:

Phép dời hình biến tam giác thành tam giác bằng nó nên các đường cao tương ứng bằng nhau.

Hướng dẫn giải:

Theo Pitago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} \) \( = \sqrt {{3^2} + {4^2}}  = 5\)

Lại có \(AH.BC = AB.AC\) \( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{3.4}}{5} = \frac{{12}}{5}\)

Phép dời hình biến tam giác ABC thành tam giác A’B’C’ nên đường cao \(A'H' = AH = \frac{{12}}{5}\).

Đáp án C

Câu 16:

Phương pháp:

Phép dời hình bảo toàn khoảng cách giữa hai điểm.

Hướng dẫn giải:

Trong các phép biến hình đã cho chỉ có phép vị tự với tỉ số \(k \ne  \pm 1\) không là phép dời hình.

Đáp án D

Câu 17:

Phương pháp:

Gọi \(\overrightarrow v  = \left( {a;b} \right)\), tìm mối quan hệ của a, b rồi đối chiếu với các đáp án.

Hướng dẫn giải:

Gọi \(\overrightarrow v  = \left( {a;b} \right)\), lấy \(M\left( {x;y} \right) \in d\) thì \(x + 3y - 4 = 0\).

\(M' = {T_{\overrightarrow v }}\left( M \right)\) \( \Rightarrow \left\{ \begin{array}{l}{x_{M'}} = x + a\\{y_{M'}} = y + b\end{array} \right.\) \( \Rightarrow M'\left( {x + a;y + b} \right)\)

\(M' \in d'\) \( \Leftrightarrow \left( {x + a} \right) + 3\left( {y + b} \right) - 11 = 0\)

\(\begin{array}{l} \Leftrightarrow x + a + 3y + 3b - 11 = 0\\ \Leftrightarrow \left( {x + 3y - 4} \right) + \left( {a + 3b - 7} \right) = 0\\ \Leftrightarrow 0 + \left( {a + 3b - 7} \right) = 0\\ \Leftrightarrow a + 3b - 7 = 0\\ \Leftrightarrow a + 3b = 7\end{array}\)

Đối chiếu các đáp án chỉ có D đúng.

Đáp án D

Câu 18:

Phương pháp:

Sử dụng định nghĩa phép vị tự \({V_{\left( {O;k} \right)}}\left( M \right) = M'\) \( \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} \)

Hướng dẫn giải:

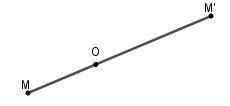
Nếu \(k < 0\) thì \(\overrightarrow {MO} \) và \(\overrightarrow {MM'} \) cùng hướng (hình vẽ).

Đáp án A

Câu 19:

Hướng dẫn giải:

\(A' = {Q_{\left( {O;\frac{\pi }{2}} \right)}}\left( A \right)\) \( \Rightarrow \left\{ \begin{array}{l}{x_{A'}} =  - {y_A} = 5\\{y_{A'}} = {x_A} = 3\end{array} \right. \Rightarrow A'\left( {5;3} \right)\)

Đáp án B

Câu 20:

Phương pháp:

Phép đồng dạng tỉ số \(k\) biến tam giác thành tam giác đồng dạng với nó theo tỉ số \(k\).

Sử dụng tính chất: Tỉ số diện tích bằng bình phương tỉ số đồng dạng.

Hướng dẫn giải:

Tam giác ABC đều cạnh 2 nên có diện tích \({S_{ABC}} = \frac{{{2^2}.\sqrt 3 }}{4} = \sqrt 3 \).

Tam giác \({A_1}{B_1}{C_1}\) đồng dạng tam giác \(ABC\) theo tỉ số \(k = 3\) nên \(\frac{{{S_{{A_1}{B_1}{C_1}}}}}{{{S_{ABC}}}} = {k^2} = 9\)

\( \Rightarrow {S_{{A_1}{B_1}{C_1}}} = 9{S_{ABC}} = 9\sqrt 3 \)

Đáp án C

Câu 21:

Hướng dẫn giải:

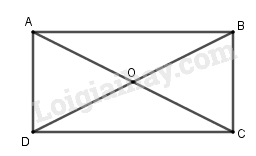
Phép quay tâm O góc quay \(\alpha  = 0,\alpha  = {180^0}\) biến hình chữ nhật ABCD thành chính nó.

Đáp án B

Câu 22:

Phương pháp:

Gọi \(I\left( {a;b} \right)\), thay vào đẳng thức véc tơ \(\overrightarrow {IM'}  =  - \frac{1}{2}\overrightarrow {IM} \) tìm a, b.

Hướng dẫn giải:

Gọi \(I\left( {a;b} \right)\)

\(M' = {V_{\left( {I; - \frac{1}{2}} \right)}}\left( M \right)\) \( \Leftrightarrow \overrightarrow {IM'}  =  - \frac{1}{2}\overrightarrow {IM} \)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 3 - a =  - \frac{1}{2}\left( {4 - a} \right)\\5 - b =  - \frac{1}{2}\left( {6 - b} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 6 - 2a =  - 4 + a\\10 - 2b =  - 6 + b\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} - 2 = 3a\\16 = 3b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a =  - \frac{2}{3}\\b = \frac{{16}}{3}\end{array} \right.\\ \Rightarrow I\left( { - \frac{2}{3};\frac{{16}}{3}} \right)\end{array}\)

Đáp án D

Câu 23:

Phương pháp:

Sử dụng biểu thức tọa độ của phép tịnh tiến: \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Hướng dẫn giải:

\(A' = {T_{\overrightarrow v }}\left( A \right)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} =  - 1 + 2 = 1\\{y_{A'}} = 2 + \left( { - 1} \right) = 1\end{array} \right.\) \( \Rightarrow A'\left( {1;1} \right)\)

Đáp án C

Câu 24:

Đáp án A

Câu 25:

Phương pháp:

Sử dụng định nghĩa phép vị tự \({V_{\left( {I;k} \right)}}\left( M \right) = M'\) \( \Leftrightarrow \overrightarrow {IM'}  = k\overrightarrow {IM} \)

Hướng dẫn giải:

\(A' = {V_{\left( {I;2} \right)}}\left( A \right) \Leftrightarrow \overrightarrow {IA'}  = k\overrightarrow {IA} \)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 = 2\left( {1 - 3} \right)\\{y_{A'}} - \left( { - 1} \right) = 2\left( {2 - \left( { - 1} \right)} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} - 3 =  - 4\\{y_{A'}} + 1 = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_{A'}} =  - 1\\{y_{A'}} = 5\end{array} \right.\\ \Rightarrow A'\left( { - 1;5} \right)\end{array}\)

Đáp án B