Đề khảo sát chất lượng đầu năm Toán 10 Chân trời sáng tạo - Đề số 1
Câu hỏi 1 :
Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có biệt thức \(\Delta {\rm{\;}} = {b^2} - 4ac < 0\). Khẳng định nào sau đây đúng?
- A Phương trình vô nghiệm.
- B Phương trình có nghiệm kép.
- C Phương trình có hai nghiệm phân biệt.
- D Phương trình có vô số nghiệm.
Đáp án: A
Lời giải chi tiết:
Do phương trình bậc hai có \(\Delta {\rm{\;}} < 0\)nên phương trình vô nghiệm.
Câu hỏi 2 :
Giải phuong trình: \({x^2} - 5x + 6 = 0.\)
- A \({x_1} = 2;{x_2} = 3.\)
- B \({x_1} = {\rm{\;}} - 1;{x_2} = {\rm{\;}} - 6.\)
- C \({x_1} = 1;{x_2} = 6.\)
- D \({x_1} = {\rm{\;}} - 2;{x_2} = {\rm{\;}} - 3.\)
Đáp án: A
Lời giải chi tiết:
Ta có: \(\Delta {\rm{\;}} = {b^2} - 4ac = 25 - 24 = 1 > 0\) Khi đó phương trình đã cho có hai nghiệm: \({x_1} = \frac{{5 - 1}}{2} = 2;{x_2} = \frac{{5 + 1}}{2} = 3\)
Câu hỏi 3 :
Trên một hệ trục toạ độ, vẽ parabol \(\left( P \right)\) có đỉnh \(O\) và đi qua \(A\left( \sqrt{3};-3 \right)\). Hoành độ điểm thuộc \(\left( P \right)\) có tung độ bằng \(-2\) là:
- A \(\left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \end{array} \right.\)
- B \(\left[ \begin{array}{l}x = \sqrt 3 \\x = - \sqrt 3 \end{array} \right.\)
- C \(\left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
- D \(\left[ \begin{array}{l}x = 2\\x = - 2\end{array} \right.\)
Đáp án: A
Phương pháp giải:
Parabol có đỉnh \(O\) nên có dạng \(y=a{{x}^{2}}\left( a\ne 0 \right)\)
Sử dụng tính chất điểm thuộc đồ thị thì toạ độ thoả mãn phương trình của hàm số
Lời giải chi tiết:
Vì parabol có đỉnh \(O\) nên có dạng \(y=a{{x}^{2}}\left( a\ne 0 \right)\).
\(\left( P \right)\) đi qua \(A\left( \sqrt{3};-3 \right)\) nên toạ độ điểm \(A\) thoả mãn phương trình hàm số.
Ta có \(-3=a{{(\sqrt{3})}^{2}}\Rightarrow a=-1\Rightarrow y=-{{x}^{2}}\).
Thay \(y=-2\) vào hàm số ta được \(-2=-{{x}^{2}}\Rightarrow {{x}^{2}}=2\Rightarrow \left[\begin{align} & x=\sqrt{2} \\ & x=-\sqrt{2} \\\end{align} \right.\)
Câu hỏi 4 :
Cho \(\widehat {xOy} = {45^0}.\) Trên tia Oy lấy hai điểm A, B sao cho \(AB = \sqrt 2 \left( {cm} \right).\) Tính độ dài hình chiếu vuông góc của đoạn thẳng AB trên Ox.
- A \(\frac{{\sqrt 2 }}{2}\left( {cm} \right).\)
- B \(\frac{{\sqrt 2 }}{4}\left( {cm} \right).\)
- C \(1\left( {cm} \right).\)
- D \(\frac{1}{2}\left( {cm} \right).\)
Đáp án: C
Lời giải chi tiết:
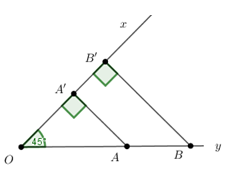
Đặt \(OA' = a,\;\;OB' = b.\)
Ta có \(\Delta OA'A\) vuông cân tại \(A' \Rightarrow OA' = AA' = a \Rightarrow OA = a\sqrt 2 .\)
\(\Delta OBB'\) vuông cân tại \(B' \Rightarrow OB' = BB' = b \Rightarrow OB = b\sqrt 2 .\)
Theo đề bài ta có: \(AB = \sqrt 2 {\rm{\;}} \Rightarrow OB = OA + \sqrt 2 {\rm{\;}} \Leftrightarrow b\sqrt 2 {\rm{\;}} = a\sqrt 2 {\rm{\;}} + \sqrt 2 \)
\( \Leftrightarrow b - a = 1 \Leftrightarrow OB' - OA' = 1 \Leftrightarrow A'B' = 1.\)
Câu hỏi 5 :
Trong các hình cho dưới đây, hình nào mô tả góc ở tâm?

- A Hình 3 và Hình 4.
- B Hình 1.
- C Hình 2.
- D Hình 1 và Hình 4
Đáp án: B
Lời giải chi tiết:
Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn. Hai cạnh của góc ở tâm cắt đường tròn ở hai điểm, hai điểm này chia đường tròn thành hai cung.
Câu hỏi 6 :
Tính bán kính r của đường tròn nội tiếp tam giác đều ABC cạnh a.
- A \(r = \frac{{a\sqrt 3 }}{6}.\)
- B \(r = a\sqrt 3 .\)
- C \(r = \frac{{a\sqrt 3 }}{3}.\)
- D \(r = \frac{{2a\sqrt 3 }}{3}.\)
Đáp án: C
Lời giải chi tiết:
Ta có đường trung tuyến trong tam giác đều cạnh a có độ dài là: \(\frac{{a\sqrt 3 }}{2}\) ‘
Khi đó bán kính r của đường tròn nội tiếp tam giác đều ABC là: \(\frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}\)
Câu hỏi 7 :
Giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là
- A \(9\)
- B \(12\)
- C \(18\)
- D \(6\)
Đáp án: C
Phương pháp giải:
Thay \(x = 3\) vào hàm số để tính giá trị của hàm số tại \(x = 3\).
Lời giải chi tiết:
Thay \(x = 3\) vào hàm số \(y = 2{x^2}\) ta có: \(y = {2.3^2} = 18\).
Vậy giá trị của hàm số \(y = 2{x^2}\) tại \(x = 3\) là \(18\).
Câu hỏi 8 :
Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - m + 3 = 0\) (m là tham số). Tìm các giá trị của m để phương trình đã cho có hai nghiệm phân biệt \({x_1},{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 10.\)
- A \(m = 1.\)
- B \(m = 4.\)
- C \(m = {\rm{\;}} - 1.\)
- D \(m = {\rm{\;}} - 4.\)
Đáp án: A
Lời giải chi tiết:
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi \(\Delta ' > 0 \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + m - 3 > 0 \Leftrightarrow m > \frac{2}{3}\)
Áp dụng hệ thức Viet ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = 2\left( {m + 1} \right)}\\{{x_1}.{x_2} = {m^2} - m + 3}\end{array}} \right.\)
Theo đề bài ta có: \(x_1^2 + x_2^2 = 10\)
\( \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} = 10\)
\( \Leftrightarrow 4{\left( {m + 1} \right)^2} - 2\left( {{m^2} - m + 3} \right) = 10\)
\( \Leftrightarrow 2{m^2} + 10m - 12 = 0\)
\( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{m = 1\left( {tm} \right)}\\{m = {\rm{\;}} - 6\left( {ktm} \right)}\end{array}} \right.\)
Câu hỏi 9 :
Chọn câu sai. Cho hình trụ có bán kính đáy là \(R\) và chiều cao \(h\) . Khi đó
- A
Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh\)
- B
Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\)
- C
Thể tích khối trụ là \(V = \pi {R^2}h\)
- D
Thể tích khối trụ là \(V = \dfrac{1}{3}\pi {R^2}h\)
Đáp án: D
Lời giải chi tiết:
Ta có hình trụ có bán kính đáy là \(R\) và chiều cao \(h\) . Khi đó
+ Diện tích xung quanh của hình trụ là \({S_{xq}} = 2\pi Rh\) nên A đúng
+ Diện tích toàn phần của hình trụ là \({S_{tp}} = 2\pi Rh + 2\pi {R^2}\) nên B đúng
+ Thể tích khối trụ là \(V = \pi {R^2}h\) nên C đúng, D sai.
Câu hỏi 10 :
Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{2x - y = 1}\\{4x + y = 5}\end{array}} \right.\)
- A \(\left( {x;y} \right) = \left( { - 1; - 1} \right).\)
- B \(\left( {x;y} \right) = \left( { - 1;1} \right).\)
- C \(\left( {x;y} \right) = \left( {1;1} \right).\)
- D \(\left( {x;y} \right) = \left( {1; - 1} \right).\)
Đáp án: C
Lời giải chi tiết:
\(\left\{ {\begin{array}{*{20}{l}}{2x - y = 1}\\{4x + y = 5}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{6x = 6}\\{y = 2x - 1}\end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 1}\\{y = 1}\end{array}} \right.\)
Vậy hệ phương trình đã cho có nghiệm là: \(\left( {x;y} \right) = \left( {1;1} \right).\)
Câu hỏi 11 :
Tìm số tự nhiên có hai chữ số, biết rằng ba lần chữ số hàng đơn vị lớn hơn chữ số hàng chục \(7\) đơn vị, và nếu viết hai chữ số ấy theo thứ tự ngược lại thì được một số mới (có hai chữ số) lớn hơn số cũ \(9\) đơn vị.
- A \(21\)
- B \(23\)
- C \(25\)
- D \(27\)
Đáp án: B
Phương pháp giải:
Gọi chữ số hàng đơn vị và hàng chục của số cần tìm là \(x\) và \(y\)\(\left( {x,y \in \mathbb{N}*,\,\,\,x,y \le 9} \right).\)
Biểu diễn các đại lượng chưa biết theo các đại lượng đã biết và các ẩn vừa gọi.
Dựa vào giả thiết của bài để lập hệ phương trình.
Giải hệ phương trình để tìm các ẩn, đối chiều với điều kiện rồi kết luận.
Lời giải chi tiết:
Gọi chữ số hàng đơn vị và hàng chục của số cần tìm là \(x\) và \(y\)\(\left( {x,y \in \mathbb{N}*,\,\,\,x,y \le 9} \right).\)
Ba lần chữ số hàng đơn vị lớn hơn chữ số hàng chục 7 đơn vị nên ta có phương trình: \(3x - y = 7\,\,\,\,\,\left( 1 \right)\)
Số cũ có dạng \(10y + x\)
Sau khi viết hai chữ số đó theo thứ tự ngược lại ta được số mới có dạng \(10x + y\)
Số mới (có hai chữ số) lớn hơn số cũ 9 đơn vị nên ta có phương trình:
\(10x + y - \left( {10y + x} \right) = 9 \Leftrightarrow 9x - 9y = 9 \Leftrightarrow x - y = 1\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}3x - y = 7\\x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x - \left( {x - 1} \right) = 7\\y = x - 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x - x + 1 = 7\\y = x - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\,\,\,\,\left( {tm} \right)\\y = 3 - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 2\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy số cần tìm là \(23.\)
Câu hỏi 12 :
Cho phương trình \({x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\) (\(m\) là tham số). Tìm \(m\) để phương tình có hai nghiệm phân biệt cùng dương.
- A \(m > 1\)
- B \(m > 3\)
- C \(m < 1\)
- D \(m < 3\)
Đáp án: B
Phương pháp giải:
Phương trình \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) có hai nghiệm phân biệt cùng dương \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} + {x_2} > 0\\{x_1}{x_2} > 0\end{array} \right..\)
Lời giải chi tiết:
Phương trình có hai nghiệm phân biệt cùng dương \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\{x_1} + {x_2} > 0\\{x_1}{x_2} > 0\end{array} \right.\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}b{'^2} - ac > 0\\\dfrac{{ - b}}{a} > 0\\\dfrac{c}{a} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - 1} \right)^2} - \left( {m - 3} \right) > 0\\2\left( {m - 1} \right) > 0\\m - 3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 2m + 1 - m + 3 > 0\\m - 1 > 0\\m > 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 4 > 0\\m > 1\\m > 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {m - \frac{3}{2}} \right)^2} + \frac{7}{4} > 0\,\,\forall m\\m > 3\end{array} \right. \Leftrightarrow m > 3\end{array}\)
Vậy \(m > 3\) thì phương trình đã cho có hai nghiệm phân biệt cùng dương.
Câu hỏi 13 :
Trong các hàm số sau, hàm số nào đồng biến với mọi \(x \in R?\)
- A \(y = {\rm{\;}} - 2x + 4.\)
- B \(y = \sqrt 3 x - 2.\)
- C \(y = {\rm{\;}} - \left( {\frac{7}{2} + 2x} \right).\)
- D \(y = \frac{{1 - x}}{3}\)
Đáp án: B
Lời giải chi tiết:
Xét các đáp án ta thấy hàm số \(y = \sqrt 3 x - 2.\) có hệ số \(a = \sqrt 3 {\rm{\;}} > 0\) . Nên hàm số này đồng biến với mọi \(x \in R.\)
Câu hỏi 14 :
Tìm giá trị của m để hàm số \(y = \left( {2m - 1} \right)x + m + 2\) cắt trục hoành tại điểm có hoành độ bằng \( - \frac{2}{3}\) .
- A \(m = {\rm{\;}} - \frac{1}{2}\)
- B \(m = \frac{1}{2}\)
- C \(m = {\rm{\;}} - 8\)
- D \(m = 8\)
Đáp án: D
Lời giải chi tiết:
Đồ thị hàm số \(y = \left( {2m - 1} \right)x + m + 2\) cắt trục hoành tại điểm có hoành độ bằng \( - \frac{2}{3}\) . Tức là điểm \(\left( { - \frac{2}{3};0} \right)\) thuộc vào đồ thị hàm số.
Khi đó ta có: \(0 = \left( {2m - 1} \right).\left( { - \frac{2}{3}} \right) + m + 2\) \( \Leftrightarrow m = 8\).
Câu hỏi 15 :
Cho các cặp số sau (0;-1),\((\sqrt{3};2-\sqrt{3})\),\((1;\sqrt{3}-3)\),\((\sqrt{3}+1;1)\). Cặp số nào không là nghiệm của phương trình \((\sqrt{3}-1)x-y=1\)?
- A (0;-1)
- B \((\sqrt{3};2-\sqrt{3})\)
- C \((1;\sqrt{3}-3)\)
- D
\((\sqrt{3}+1;1)\)
Đáp án: C
Phương pháp giải:
Thay các cặp số đã cho vào phương trình. Cặp nào thỏa mãn thì là nghiệm của phương trình đã cho.
Lời giải chi tiết:
\((\sqrt{3}-1)x-y=1\,\,\,\,\,\,(1)\)
Thay x = 0, y = -1 vào vế trái của (1) ta được: \((\sqrt{3}-1).0-(-1)=0+1=1\) .
Vậy (0; -1) là nghiệm của (1).
Thay \((\sqrt{3},2-\sqrt{3})\) vào vế trái của (1) ta được: \((\sqrt{3}-1).\sqrt{3}-(2-\sqrt{3})=3-\sqrt{3}-2+\sqrt{3}=1\).
Vậy \((\sqrt{3},2-\sqrt{3})\) là nghiệm của (1).
Thay \((1;\sqrt{3}-3)\) vào vế trái của (1) ta được: \((\sqrt{3}-1).1-(\sqrt{3}-3)=\sqrt{3}-1-\sqrt{3}+3=2\ne 1\).
Vậy \((1;\sqrt{3}-3)\)không là nghiệm của (1).
Thay \((\sqrt{3}+1;1)\) vào vế trái của (1) ta được: \((\sqrt{3}-1).(\sqrt{3}+1)-1=3-1-1=1\).
Vậy \((\sqrt{3}+1;1)\) là nghiệm của (1).
Câu hỏi 16 :
Cho hàm số \(y=\dfrac{1}{2}{{x}^{2}}\) có đồ thị (P) và đường thẳng (d): \(y=3mx-2\).Tìm m để đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt.
- A
\(m<\dfrac{-2}{3}\)
- B
\(m>\dfrac{2}{3}\)
- C
\(m<\dfrac{-2}{3}\) hoặc \(m>\dfrac{2}{3}\)
- D
\(\dfrac{-2}{3}<m<\dfrac{2}{3}\)
Đáp án: C
Phương pháp giải:
Lập phương trình hoành độ giao điểm của (P) và (d). Áp dụng điều kiện để phương trình bậc hai có hai nghiệm phân biệt. Từ đó tìm giá trị của tham số m.
Lời giải chi tiết:
Xét phương trình hoành độ giao điểm của (P) và (d):
\(\begin{align} & \,\,\,\,\,\,\,\frac{1}{2}{{x}^{2}}=3mx-2 \\ & \Leftrightarrow {{x}^{2}}-6mx+4=0\,\,\,\,\,\,\,(1) \\ \end{align}\)
Để (d) và (P) có 2 giao điểm thì phương trình (1) có 2 nghiệm phân biệt:
\(\begin{array}{l}
\Leftrightarrow \Delta ' > 0\\
\Leftrightarrow 9{m^2} - 4 > 0\\
\Leftrightarrow (3m - 2)(3m + 2) > 0
\end{array}\)
\(\Leftrightarrow m<\dfrac{-2}{3}\) hoặc \(m>\dfrac{2}{3}\).
Vậy với \(m<\dfrac{-2}{3}\) hoặc \(m>\dfrac{2}{3}\) thì đường thẳng (d) luôn cắt (P) tại 2 điểm phân biệt.
Câu hỏi 17 :
Tìm các giá trị của a sao cho \(\frac{{a - 1}}{{\sqrt a }} < 0.\)
- A \(a \ge 0\)
- B \(0 \le a < 1\)
- C \(a < 1\)
- D \(0 < a < 1\)
Đáp án: D
Lời giải chi tiết:
\(\frac{{a - 1}}{{\sqrt a }} < 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a - 1 < 0}\\{a > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a < 1}\\{a > 0}\end{array}} \right.\)
Câu hỏi 18 :
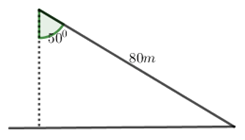
Bạn An chơi thả diều. Tại thời điểm dây diều dài 80(m) và tạo với phương thẳng đứng một góc \({50^0}\) . Tính khoảng cách d từ diều đến mặt đất tại thời điểm đó (giả sử dây diều căng và không giãn; kết quả làm tròn đến chữ số thập phân thứ hai).
- A \(d \approx 51,42\left( m \right).\)
- B \(d \approx 57,14\left( m \right).\)
- C \(d \approx 54,36\left( m \right).\)
- D \(d \approx 61,28\left( m \right).\)
Đáp án: A
Lời giải chi tiết:
Ta có: \(\cos {50^0} = \frac{d}{{80}} \Rightarrow d \approx 51,42\left( m \right)\)
Câu hỏi 19 :
Cho đường thẳng \(d\) cắt đường tròn \(\left( O \right)\) tại hai điểm phân biệt \(A;\,\,B.\) Biết khoảng cách từ điểm \(O\) đến đường thẳng \(d\) bằng \(3cm\) và độ dài đoạn thẳng \(AB\) bằng \(8cm.\) Bán kính của đường tròn \(\left( O \right)\) bằng:
- A \(7cm\)
- B \(11cm\)
- C \(73cm\)
- D \(5cm\)
Đáp án: D
Phương pháp giải:
Sử dụng mối liên hệ giữa đường kính và dây cung
Sử dụng định lý Pytago để tính toán
Lời giải chi tiết:
_co_OH=3cm.png)
Kẻ \(OH \bot AB.\)
Khi đó ta có \(H\) là trung điểm của \(AB.\) (mối liên liên hệ giữa đường kính và dây cung)
\( \Rightarrow \left\{ \begin{array}{l}OH = 3cm\\AH = \dfrac{1}{2}AB = 4cm\end{array} \right..\)
Áp dụng định lý Py-ta-go cho \(\Delta AOH\) vuông tại \(H\) ta có:
\(\begin{array}{l}O{A^2} = A{H^2} + H{O^2} = {4^2} + {3^2} = 25\\ \Rightarrow R = OA = 5cm.\end{array}\)
Câu hỏi 20 :
Cho \(\Delta ABC\) vuông tại \(A\) có đường cao \(AH\)và đường trung tuyến \(AM\). Biết \(AH = 3cm;\,HB = 4cm.\) Hãy tính \(AB,AC,AM\) và diện tích tam giác \(ABC.\)
- A
\(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\)\({S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
- B
\(AB = 5cm,\,\,AC = 3cm,\,\,AM = 4cm,\)\({S_{\Delta ABC}} = \dfrac{{39}}{4}\,\,c{m^2}\)
- C
\(AB = \dfrac{{14}}{3}cm,\,\,AC = \dfrac{{14}}{4}cm,\,\,AM = 3cm,\)\({S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
- D
\(AB = \dfrac{{14}}{3}cm,\,\,AC = 3cm,\,\,AM = \dfrac{{27}}{8}cm,\)\({S_{\Delta ABC}} = 9\,\,c{m^2}\)
Đáp án: A
Phương pháp giải:
Sử dụng định lý Pytago, hệ thức lượng trong tam giác vuông và công thức tính diện tích tam giác.
Lời giải chi tiết:
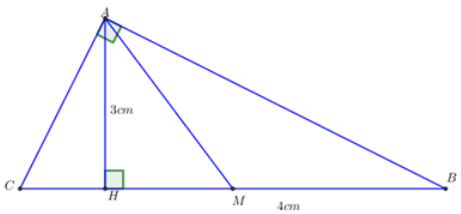
+) Áp dụng định lý Pytago trong tam giác vuông ABH vuông tại H ta có:
\(\,\,\,\,\,\,\,A{B^2} = A{H^2} + H{B^2} = {3^2} + {4^2} = 25 \Rightarrow AB = 5\,\,\,\left( {cm} \right)\).
+) Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ABC với AH là đường cao ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{A{H^2}}} - \dfrac{1}{{A{B^2}}} \Leftrightarrow \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{3^2}}} - \dfrac{1}{{{5^2}}} = \dfrac{{16}}{{225}} \Rightarrow AC = \dfrac{{15}}{4}\left( {cm} \right)\)
+) Áp dụng định lý Pytago trong tam giác vuông ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {\left( {\dfrac{{15}}{4}} \right)^2} = \dfrac{{625}}{{16}} \Rightarrow BC = \dfrac{{25}}{4}\left( {cm} \right)\).
+) Tam giác ABC vuông tại A có trung tuyến AM nên ta có: \(AM = \dfrac{1}{2}BC = \dfrac{{25}}{8}\,\,\,\left( {cm} \right)\)
+) Diện tích tam giác ABC với AH là đường cao ta có: \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.3.\dfrac{{25}}{4} = \dfrac{{75}}{8}\,\,\left( {c{m^2}} \right)\).
Vậy \(AB = 5cm,\,\,AC = \dfrac{{15}}{4}cm,\,\,AM = \dfrac{{25}}{8}cm,\,\,{S_{\Delta ABC}} = \dfrac{{75}}{8}\,\,c{m^2}\)
Câu hỏi 21 :
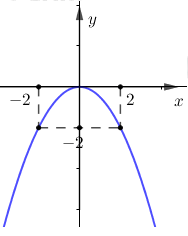
Đồ thị ở hình bên là đồ thị hàm số nào trong các hàm số sau:
- A \(y = {\rm{\;}} - 2{x^2}\)
- B \(y = {\rm{\;}} - \frac{1}{4}{x^2}\)
- C \(y = {\rm{\;}} - 4{x^2}\)
- D \(y = {\rm{\;}} - \frac{1}{2}{x^2}\)
Đáp án: D
Lời giải chi tiết:
Giả sử hàm số có dạng: \(y = a{x^2}\) . Ta có điểm \(\left( {2; - 2} \right)\) thuộc đồ thị đã cho nên: \( - 2 = a{.2^2} \Rightarrow a = \frac{{ - 1}}{2}\)
Vậy hàm số cần tìm là: \(y = {\rm{\;}} - \frac{1}{2}{x^2}\)
Câu hỏi 22 :
Cho \(P = \sqrt {{{\left( {\sqrt 3 {\rm{\;}} + 1} \right)}^2}} {\rm{\;}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} \) . Khẳng định nào sau đây đúng?
- A \(P = 2\)
- B \(P = 2 + 2\sqrt 3 \)
- C \(P = 2 - \sqrt 3 \)
- D \(2\sqrt 3 \)
Đáp án: D
Lời giải chi tiết:
\(P = \sqrt {{{\left( {\sqrt 3 {\rm{\;}} + 1} \right)}^2}} {\rm{\;}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}} {\rm{\;}}\)
\(\;\;\; = \left| {\sqrt 3 {\rm{\;}} + 1} \right| + \left| {1 - \sqrt 3 } \right|\)
\(\;\;\; = \sqrt 3 {\rm{\;}} + 1 + \sqrt 3 {\rm{\;}} - 1 = 2\sqrt 3 \) \(\left( {do{\mkern 1mu} {\mkern 1mu} \sqrt 3 {\rm{\;}} + 1 > 0;{\mkern 1mu} 1 - \sqrt 3 {\rm{\;}} < 0} \right)\)
Câu hỏi 23 :
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
- A \(0\)
- B \(1\)
- C \(2\)
- D \(3\).
Đáp án: C
Phương pháp giải:
Vị trí tương đối của đường tròn tâm \(O\) bán kính \(R\) và đường thẳng \(a:\)
+) Nếu \(d\left( {O;\,\,a} \right) < R \Rightarrow a\) cắt đường tròn tại hai điểm phân biệt.
+) Nếu \(d\left( {O;\,\,a} \right) = R \Rightarrow a\) tiếp xúc với đường tròn tại 1 điểm.
+) Nếu \(d\left( {O;\,\,a} \right) > R \Rightarrow a\) không cắt đường tròn.
Lời giải chi tiết:
.png) Ta có: \(d\left( {O;\,\,a} \right) = \sqrt 8 ;\,\,\,\,R = 3 \Rightarrow d\left( {O;\,\,a} \right) < R\)
Ta có: \(d\left( {O;\,\,a} \right) = \sqrt 8 ;\,\,\,\,R = 3 \Rightarrow d\left( {O;\,\,a} \right) < R\)
Nên đường thẳng \(a\) cắt đường tròn \(\left( {O;\,\,R} \right)\) tại hai điểm phân biệt.
Câu hỏi 24 :
Cho hình thang cân \(ABCD\,\,\,\left( {AB\parallel CD} \right);\) \(CD = 2AD = 2AB = 8\). Tính diện tích của hình thang đó.
- A \(12\sqrt 2 \)
- B \(12\sqrt 3 \)
- C \(12\)
- D \(12\sqrt 6 \)
Đáp án: B
Phương pháp giải:
- Kẻ \(AH,\,\,BK\) cùng vuông góc với \(CD\) \(\left( {H,\,\,K \in CD} \right)\). Chứng minh \(ABKH\) là hình chữ nhật.
- Tính \(DH,\,\,CK\).
- Áp dụng định lí Pytago tính \(AH\).
- Tính diện tích hình thang: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\).
Lời giải chi tiết:
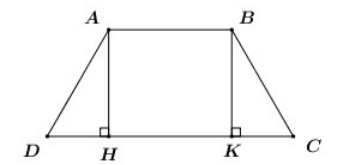
Kẻ \(AH,\,\,BK\) cùng vuông góc với \(CD\) \(\left( {H,\,\,K \in CD} \right)\).
Xét tứ giác \(ABKH\) có: \(\left\{ \begin{array}{l}AB\parallel HK\\AH\parallel BK\end{array} \right.\), suy ra \(ABKH\) là hình bình hành.
Lại có \(\angle AHK = {90^0}\) nên \(ABKH\) là hình chữ nhật, do đó \(HK = AB = 4\).
Xét \(\Delta ADH\) và \(\Delta BCK\) có:
\(\angle AHD = \angle BKC = {90^0}\);
\(AD = BC\) (tính chất hình thang cân);
\(\angle ADH = \angle ACK\) (tính chất hình thang cân).
\( \Rightarrow \Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn) \( \Rightarrow DH = CK\) (hai cạnh tương ứng).
Mà \(DH + CK = CD - HK = 8 - 4 = 4\).
Do đó \(DH = CK = 2\).
Áp dụng định lí Pytago trong tam giác vuông \(ADH\) ta có:
\(A{H^2} = A{D^2} - D{H^2}\) \( \Leftrightarrow A{H^2} = {4^2} - {2^2} = 12\) \( \Leftrightarrow AH = 2\sqrt 3 \).
Vậy diện tích hình thang \(ABCD\) là: \({S_{ABCD}} = \dfrac{{\left( {AB + CD} \right).AH}}{2}\) \( = \dfrac{{\left( {4 + 8} \right).2\sqrt 3 }}{2} = 12\sqrt 3 \).
Câu hỏi 25 :
Tính thể tích V của hình cầu có bán kính \(R = 3\left( {cm} \right).\)
- A \(V = 108\pi \left( {c{m^3}} \right)\)
- B \(V = 9\pi \left( {c{m^3}} \right)\)
- C \(V = 72\pi \left( {c{m^3}} \right)\)
- D \(V = 36\pi \left( {c{m^3}} \right)\)
Đáp án: D
Lời giải chi tiết:
Áp dụng công thức tính thể tích hình cầu ta có: \(V = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.3^3} = 36\pi \left( {c{m^3}} \right)\)
Câu hỏi 26 :
Cho hai đường tròn (O) và (O’) cắt nhau tại A, B. Tiếp tuyến tại A của đường tròn (O’) cắt (O) tại C và của (O) cắ (O’) tại D. Biết \(\widehat {ABC} = {75^0}\) . Tính \(\widehat {ABD}?\)
A. \(\widehat {ABD} = {40^0}.\)
- B \(\widehat {ABD} = {150^0}.\)
- C \(\widehat {ABD} = {50^0}.\)
- D \(\widehat {ABD} = {75^0}.\)
Đáp án: D
Lời giải chi tiết:
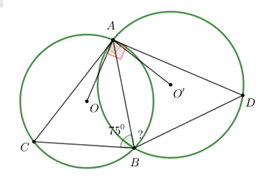
Xét tam giác ABC và tam giác DBA có:
\(\widehat {CAB} = \widehat {ADB}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung của
đường tròn (O’) cùng chắn cung AB)
\(\widehat {ACB} = \widehat {BAD}\)(góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung của
đường tròn (O) cùng chắn cung AB)
Vậy \(\Delta ABC\~\Delta DBA\) (g-g)
Khi đó ta có: \(\widehat {ABC} = \widehat {ABD} = {75^0}\)(2 góc tương ứng)
Câu hỏi 27 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
- A
\(\dfrac{3}{4}\)
- B
\(\dfrac{3}{5}\)
- C
\(\dfrac{4}{3}\)
- D
\(\dfrac{4}{5}\)
Đáp án: D
Phương pháp giải:
- Áp dụng định lí Pi-ta-go để tìm độ dài cạnh \(BC\).
- Sử dụng định nghĩa: \(cos\alpha \) = cạnh kề : cạnh huyền.
Lời giải chi tiết:
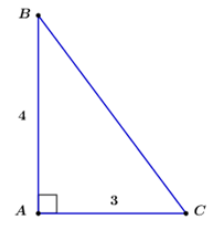
Tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pi-ta-go ta có:
\(B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 25 \Rightarrow BC = 5\)
Khi đó \(\cos B = \dfrac{{AB}}{{BC}} = \dfrac{4}{5}\)
Câu hỏi 28 :
Giá trị của biểu thức \(P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\) bằng
- A \(0\)
- B \(1\)
- C \(2\)
- D \(3\)
Đáp án: C
Phương pháp giải:
+) Sử dụng công thức: \(\sin \alpha = \cos \left( {{{90}^0} - \alpha } \right);\;\;{\sin ^2}\alpha + {\cos ^2}\alpha = 1.\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}P = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\cos ^2}{50^0} + {\cos ^2}{70^0}\\ = {\cos ^2}{20^0} + {\cos ^2}{40^0} + {\sin ^2}{40^0} + {\sin ^2}{20^0}\\ = \left( {{{\cos }^2}{{20}^0} + {{\sin }^2}{{20}^0}} \right) + \left( {{{\cos }^2}{{40}^0} + {{\sin }^2}{{40}^0}} \right)\\ = 1 + 1 = 2.\end{array}\)
Câu hỏi 29 :
Cho hàm số \(y = ax\) có đồ thị như hình bên. Giá trị của \(a\) bằng:
- A \(a = 3\)
- B \(a = - 3\)
- C
\(a = \dfrac{1}{3}\)
- D
\(a = - \dfrac{1}{3}\)
Đáp án: C
Phương pháp giải:
Thay tọa độ điểm thuộc đồ thị vào hàm số để tìm hệ số \(a\)
Lời giải chi tiết:
Ta thấy \(M\left( {3;1} \right)\) thuộc đồ thị hàm số nên \(1 = a.3 \Leftrightarrow a = \dfrac{1}{3}\)
Câu hỏi 30 :
Tìm số tự nhiên n có hai chữ số, biết rằng tổng các chữ số của nó bằng 9 và nếu cộng thêm vào số đó 63 đơn vị thì được một số mới cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại.
- A n = 36
- B n = 18
- C n = 45
- D n = 27
Đáp án: B
Lời giải chi tiết:
Gọi số tự nhiên n có hai chữ số là: \(\overline {ab} {\mkern 1mu} {\mkern 1mu} \left( {a \ne 0,a,b \in N} \right)\)
Tổng các chữ số của nó bằng 9 nên ta có: \(a + b = 9{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
Nếu thêm vào số đó 63 đơn vị thì được một số mới cũng viết bằng hai chữ số đó nhưng theo thứ tự ngược lại. Nên ta có phương trình:
\(\begin{array}{*{20}{l}}{\;\;\;\;\overline {ab} {\rm{\;}} + 63 = \overline {ba} {\rm{\;}} \Leftrightarrow 10a + b + 63 = 10b + a}\\{ \Leftrightarrow 9a - 9b = {\rm{\;}} - 63 \Leftrightarrow a - b = {\rm{\;}} - 7{\mkern 1mu} {\mkern 1mu} \;\;\left( 2 \right)}\end{array}\)
Từ (1) và (2) ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{a + b = 9}\\{a - b = {\rm{\;}} - 7}\end{array}} \right.\left\{ {\begin{array}{*{20}{l}}{a = 1}\\{b = 8}\end{array}} \right. \Rightarrow \overline {ab} {\rm{\;}} = 18\)
Vậy số cần tìm là: n = 18.
Câu hỏi 31 :
Phân tích đa thức \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\) thành nhân tử ta được:
- A
\(5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
- B
\(5{x^2}{y^3}\left( { - 5xy + 2x} \right)\)
- C
\({x^2}{y^3}\left( {1 - 5xy + 2x} \right)\)
- D
\(5{x^2}{y^3}\left( {1 - xy + x} \right)\)
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử.
Lời giải chi tiết:
Ta có: \(5{x^2}{y^3} - 25{x^3}{y^4} + 10{x^3}{y^3}\)\( = 5{x^2}{y^3}. 1 - 5{x^2}{y^3}. 5xy + 5{x^2}{y^3}. 2x\)\( = 5{x^2}{y^3}\left( {1 - 5xy + 2x} \right)\).
Câu hỏi 32 :
Cho các biểu thức : \(P = \left( {\dfrac{{3\sqrt x }}{{x\sqrt x + 1}} - \dfrac{{\sqrt x }}{{x - \sqrt x + 1}} + \dfrac{1}{{\sqrt x + 1}}} \right):\dfrac{{\sqrt x + 3}}{{x - \sqrt x + 1}}\,\,\,\left( {x \ge 0} \right)\)
Rút gọn biểu thức \(P.\) Tìm các giá trị của \(x\) để \(P \ge \dfrac{1}{5}\).
- A
\(P = \dfrac{1}{\sqrt{x} + 3}\,\,;\,\,0 \le x \le 4\)
- B
\(P = \dfrac{1}{\sqrt{x} + 3}\,\,;\,\,0 \le x \le 2\)
- C
\(P = \dfrac{1}{\sqrt{x} + 1}\,\,;\,\,0 \le x \le 2\)
- D
\(P = \dfrac{1}{\sqrt{x} + 1}\,\,;\,\,0 \le x \le 4\)
Đáp án: A
Phương pháp giải:
Quy đồng mẫu các phân thức, rút gọn biểu thức đã cho.
Giải bất phương trình \(P \ge \frac{1}{5},\) tìm \(x.\) Đối chiếu với điều kiện rồi kết luận.
Lời giải chi tiết:
Điều kiện: \(x \ge 0.\)
\(\begin{array}{l}P = \left( {\dfrac{{3\sqrt x }}{{x\sqrt x + 1}} - \dfrac{{\sqrt x }}{{x - \sqrt x + 1}} + \dfrac{1}{{\sqrt x + 1}}} \right):\dfrac{{\sqrt x + 3}}{{x - \sqrt x + 1}}\\\,\,\,\, = \left[ {\dfrac{{3\sqrt x }}{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}} - \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}} + \dfrac{{x - \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}} \right]:\dfrac{{\sqrt x + 3}}{{x - \sqrt x + 1}}\\\,\,\,\, = \dfrac{{3\sqrt x - x - \sqrt x + x - \sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}.\dfrac{{x - \sqrt x + 1}}{{\sqrt x + 3}}\\\,\,\,\, = \dfrac{{\sqrt x + 1}}{{\left( {\sqrt x + 1} \right)\left( {x - \sqrt x + 1} \right)}}.\dfrac{{x - \sqrt x + 1}}{{\sqrt x + 3}} \\= \dfrac{1}{{\sqrt x + 3}}.\end{array}\)
\(\begin{array}{l} \Rightarrow P \ge \dfrac{1}{5} \Leftrightarrow \dfrac{1}{{\sqrt x + 3}} \ge \dfrac{1}{5}\\ \Leftrightarrow \dfrac{1}{{\sqrt x + 3}} - \dfrac{1}{5} \ge 0 \Leftrightarrow \dfrac{{5 - \sqrt x - 3}}{{5\left( {\sqrt x + 3} \right)}} \ge 0\\ \Leftrightarrow \dfrac{{2 - \sqrt x }}{{5\left( {\sqrt x + 3} \right)}} \ge 0 \Leftrightarrow 2 - \sqrt x \ge 0\\ \Leftrightarrow \sqrt x \le 2 \Leftrightarrow x \le 4\end{array}\)
Vậy \(0 \le x \le 4\) thỏa mãn bài toán.
Câu hỏi 33 :
\(x = - 2\) là một nghiệm của bất phương trình nào dưới đây?
- A
\(3x + 17 < 5\)
- B
\( - 2x + 1 < - 1\)
- C
\(\dfrac{1}{2}x + 5 > 3,5\)
- D
\(1 - 2x < - 3\)
Đáp án: C
Phương pháp giải:
Giải từng bất đẳng thức trong 4 đáp án, chọn đáp án mà bất đẳng thức có nghiệm \(x = - 2\) nằm trong tập nghiệm.
Lời giải chi tiết:
Xét từng đáp án ta có:
\(3x + 17 < 5 \Leftrightarrow 3x < - 12 \Leftrightarrow x < - 4 \Rightarrow \) A sai.
\( - 2x + 1 < - 1 \Leftrightarrow - 2x < - 2 \Leftrightarrow x > 1 \Rightarrow \) B sai.
\(\dfrac{1}{2}x + 5 > 3,5 \Leftrightarrow \dfrac{1}{2}x > - 1,5 \Leftrightarrow x > - 3 \Rightarrow x = - 2\) là một nghiệm của bất phương trình \( \Rightarrow \) C đúng.
\(1 - 2x < - 3 \Leftrightarrow - 2x < - 4 \Leftrightarrow x > 2 \Rightarrow \) D sai.
Câu hỏi 34 :
Tìm tất cả các giá trị của m để đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành.
- A \(m < {\rm{\;}} - \frac{1}{2}\)
- B \(m > {\rm{\;}} - \frac{1}{2}\)
- C \(m \ge {\rm{\;}} - \frac{1}{2}\)
- D \(m \le {\rm{\;}} - \frac{1}{2}\)
Đáp án: A
Lời giải chi tiết:
Đồ thị hàm số \(y = \left( {2m + 1} \right){x^2}\) nằm phía dưới trục hoành tức là \(y < 0 \Leftrightarrow 2m + 1 < 0\)
\( \Leftrightarrow m < {\rm{\;}} - \frac{1}{2}{\mkern 1mu} {\mkern 1mu} \left( {Do{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {x^2} \ge 0} \right)\)
Câu hỏi 35 :
Cho \(\Delta MNP \backsim \Delta HGK\) có tỉ số chu vi: \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}.\) Chọn câu đúng.
- A
\(\dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
- B
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{2}{7}\)
- C
\(\dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = \dfrac{{49}}{4}\)
- D
\(\dfrac{{NP}}{{GK}} = \dfrac{5}{7}\)
Đáp án: A
Phương pháp giải:
+) Áp dụng lý thuyết về mối quan hệ giữa tỉ số diện tích hai tam giác đồng dạng và tỉ số đồng dạng của 2 tam giác, kết hợp với dữ kiện đề bài cho để thực hiện yêu cầu của bài toán.
Lưu ý: Tỉ số đồng dạng bằng tỉ số chu vi và tỉ số diện tích bằng bình phương tỉ số đồng dạng.
Lời giải chi tiết:
Gọi k là tỉ số đồng dạng của 2 tam giác MNP và HGK.
Theo bài ta có:
\(\Delta MNP \backsim \Delta HGK\) và \(\dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7}\)
\( \Rightarrow \dfrac{{MN}}{{HG}} = \dfrac{{NP}}{{GK}} = \dfrac{{MP}}{{HK}} \)\(=\dfrac{MN+NP+MP}{HG+GK+HK}= \dfrac{{{P_{\Delta MNP}}}}{{{P_{\Delta HGK}}}} = \dfrac{2}{7} = k\)
Do đó: \( \dfrac{{HG}}{{MN}} = \dfrac{7}{2}\)
Và \( \dfrac{{{S_{\Delta MNP}}}}{{{S_{\Delta HGK}}}} = {k^2} = {\left( {\dfrac{2}{7}} \right)^2} = \dfrac{4}{{49}}.\)
Câu hỏi 36 :
Hai vòi nước cùng chảy vào một bể không có nước. Nếu cho vòi một chảy trong 3 giờ rồi hóa lại, sau đó cho vòi hai chảy tiếp trong 8 giờ nữa thì đầy bể. Nếu cho vòi một chảy trong 1 giờ, rồi cho cả hai vòi chảy tiếp trong 4 giờ nữa thì số nước chảy vào bằng \(\frac{8}{9}\) bể. Hỏi nếu chảy một mình thì vòi một sẽ chảy trong thời gian t bằng bao nhiêu thì đầy bể?
- A t = 10 giờ. B. t = 12 giờ.
- C t = 11 giờ. D. t = 9 giờ.
Đáp án: D
Lời giải chi tiết:
Gọi thời gian chảy một mình đầy bể của vòi 1 là: x (giờ) (x>3)
Thời gian chảy một mình đầy bể của vòi 2 là: y (giờ) (y > 8)
Mỗi giờ vòi 1 sẽ chảy được: \(\frac{1}{x}\) (bể)
Mỗi giờ vỏi 2 sẽ chảy được: \(\frac{1}{y}\) (bể)
Theo bài ra ta có: \(\frac{3}{x} + \frac{8}{y} = 1\left( 1 \right)\)
Vòi 1 chảy được 5 giờ, vòi 2 chảy được 4 giờ sẽ được \(\frac{8}{9}\) bể nên ta có phương trình: \(\frac{5}{x} + \frac{4}{y} = \frac{8}{9}\left( 2 \right)\)
Từ (1) và (2) giải hệ phương trình ta tìm được x = 9; y = 12 (giờ)
Câu hỏi 37 :
Căn bậc hai số học của 4 là:
- A
\( - 2\)
- B
\(2\)
- C
\(16\)
- D
\( \pm 2\)
Đáp án: B
Phương pháp giải:
Căn bậc hai số học của số \(a\) không âm là số \(x\) không âm sao cho \({x^2} = a.\)
Kí hiệu: \(x = \sqrt a .\)
Lời giải chi tiết:
Vì \({2^2} = 4\) và \(2 > 0\) nên \(\sqrt 4 = 2.\)
Câu hỏi 38 :
Cho phương trình \(m{x^2} + 4(m - 1)x + 2m - 2 = 0\) có nghiệm bằng 1 nếu m nhận giá trị nào dưới đây ?
- A
\(\displaystyle {7 \over 6}\)
- B
\(-\displaystyle {7 \over 6}\)
- C
\(-\displaystyle {6 \over 7}\)
- D
\(\displaystyle {6 \over 7}\)
Đáp án: D
Phương pháp giải:
Dựa vào tính chất nếu \(x = {x_0}\) là nghiệm của phương trình \(f\left( x \right) = 0\) thì \(f\left( {{x_0}} \right) = 0\)
Lời giải chi tiết:
Phương trình \(m{x^2} + 4(m - 1)x + 2m - 2 = 0\) có nghiệm 1 thì m phải thoả mãn phương trình
Thay x = 1 vào phương trình ta được:
\(m{.1^2} + 4(m - 1).1 + 2m - 2 = 0 \Leftrightarrow m + 4m - 4 + 2m - 2 = 0 \Leftrightarrow 7m - 6 = 0 \)\(\displaystyle \Leftrightarrow m = {6 \over 7}\)
Câu hỏi 39 :
Một hình hộp chữ nhật có thể tích \(192cm^3,\) mặt đáy có chiều dài 6cm và chiều rộng $4cm.$ Chiều cao hình hộp chữ nhật đó là:
- A
\(7\,cm\)
- B
\(9\,cm\)
- C
\(6\,cm\)
- D
\(8\,cm\)
Đáp án: D
Phương pháp giải:
Sử dụng công thức tính thể tích hình hộp chữ nhật có chiều dài, chiều rộng và chiều cao lần lượt là \(a,b,c\) là \(V = abc.\)
Lời giải chi tiết:
Hình hộp chữ nhật có chiều dài \(a = 6cm,\) chiều rộng \(b = 4cm\) và chiều cao \(c.\)
Thể tích hình hộp chữ nhật \(V = abc\) \( = 6.4.c\)
Theo đề bài ta có \(6.4.c = 192 \Leftrightarrow c = 8\,cm.\)
Vậy chiều cao cần tìm là \(8\,cm.\)
Câu hỏi 40 :
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) tiếp xúc ngoài tại \(A\). Kẻ tiếp tuyến chung ngoài \(BC,B \in \left( O \right)\) và \(C \in (O')\). Tiếp tuyến chung trong tại \(A\) cắt tiếp tuyến chung ngoài \(BC\) tại \(I\). Tính độ dài \(BC\) biết \(OA = 9cm,O'A = 4cm\).
- A \(12cm\)
- B \(18cm\)
- C \(10cm\)
- D
\(6cm\)
Đáp án: A
Phương pháp giải:
Sử dụng tính chất hai tiếp tuyến cắt nhau
Sử dụng công thức lượng giác
Lời giải chi tiết:
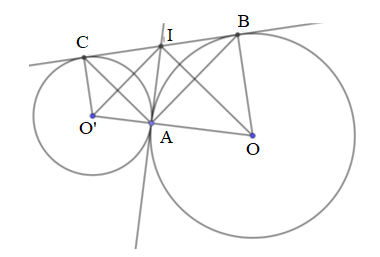
Ta có \(IO\) là tia phân giác của \(\widehat {BIA}\)
\(IO'\) là tia phân giác của \(\widehat {CIA}\)
Mà \(\widehat {BIA} + \widehat {CIA} = {180^0} \Rightarrow \widehat {OIO'} = {90^0}\)
Tam giác \(OIO'\) vuông tại \(I\) có \(IA\) là đường cao nên \(I{A^2} = AO.AO' = 9.4 = 36 \Rightarrow IA = 6cm\).
\( \Rightarrow IA = IB = IC = 6cm\) (tính chất hai tiếp tuyến cắt nhau)
Vậy \(BC = 2IA = 2.6 = 12\left( {cm} \right)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Đề khảo sát chất lượng đầu năm Toán 10 Chân trời sáng tạo - Đề số 1 timdapan.com"







