Đề cương lý thuyết học kì 1 - Vật lí 12

Chương 1

CHƯƠNG 1: DAO ĐỘNG CƠ

I. Dao động điều hòa

1. Định nghĩa về dao động điều hòa

- Dao động là chuyển động qua lại quanh vị trí cân bằng.

- Dao động tuần hoàn là dao động được lặp lại như cũ sau những khoảng thời gian bằng nhau.

- Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hay sin) của thời gian.

2. Các đại lượng trong dao động điều hòa

a) Các đại lượng dao động:

- Li độ: \(x = Acos\left( {\omega t + \varphi } \right)\)

- Vận tốc: \(v = x' = \omega Acos\left( {\omega t + \varphi {\rm{\;}} + \frac{\pi }{2}} \right)\)

- Gia tốc: \(a = v' = x'' = {\omega ^2}Acos\left( {\omega t + \varphi {\rm{\;}} + \pi } \right)\)

- Lực kéo về: \(F = ma = m{\omega ^2}Acos\left( {\omega t + \varphi {\rm{\;}} + \pi } \right)\)

b) Các dạng năng lượng trong dao động:

- Thế năng: \({{\rm{W}}_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{x^2}\)

- Động năng: \({{\rm{W}}_d} = \frac{1}{2}m{v^2}\)

- Cơ năng: \({\rm{W}} = {{\rm{W}}_t} + {{\rm{W}}_d} = \frac{1}{2}k{A^2} = \frac{1}{2}m{\omega ^2}A = \frac{1}{2}mv_{{\rm{max}}}^2\)

- Khi \({{\rm{W}}_d} = n{{\rm{W}}_t} \to x = {\rm{\;}} \pm \frac{A}{{\sqrt {n + 1} }}\)

c) Chú ý:

- Tốc độ trung bình trong một chu kì: \({v_{tb}} = \frac{{4A}}{T} = \frac{{2\omega A}}{\pi } = \frac{{2{v_{\max }}}}{\pi }\)

- Cứ sau khoảng thời gian ngắn nhất \(\frac{T}{4}\) thì vật lại có \({{\rm{W}}_d} = {{\rm{W}}_t}\)

- Hệ thức độc lập với thời gian: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)

II. Con lắc lò xo

- Con lắc lò xo là một hệ dao động điều hòa.

- Tần số góc, chu kì, tần số:

\(\omega  = \sqrt {\frac{k}{m}} ;T = 2\pi \sqrt {\frac{m}{k}} ;f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} \)

Với con lắc lò xo thẳng đứng \(\omega  = \sqrt {\frac{g}{{\Delta {l_0}}}} ;T = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \)

( \(\Delta {l_0} = \frac{{mg}}{k}\) là độ giãn của lò xo ở VTCB )

- Biên độ: \(A = {l_{\max }} - {l_{cb}};A = \frac{{{l_{\max }} - {l_{\min }}}}{2}\) với \({l_{cb}} = \frac{{{l_{\max }} + {l_{\min }}}}{2}\)

- Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một.

- Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng:

 

+ Độ lớn lực đàn hồi có biểu thức:

\({F_{dh}} = k\left| {\Delta {l_0} + x} \right|\) với chiều dương hướng xuống

\({F_{dh}} = k\left| {\Delta {l_0} - x} \right|\) với chiều dương hướng lên.

+ Lực đàn hồi cực đại (lực kéo):

\({F_{\max }} = k\left( {\Delta {l_0} + A} \right)\) (lúc vật ở vị trí thấp nhất)

+ Lực đàn hồi cực tiểu:

Nếu \(A < \Delta {l_0} \Rightarrow {F_{\min }} = k\left( {\Delta {l_0} - A} \right)\)

Nếu \(A \ge \Delta {l_0} \Rightarrow {F_{\min }} = 0\) (lúc vật đi qua vị trí lò xo không biến dạng).

+ Lực đẩy (lực nén) đàn hồi cực đại: \({F_n}\max  = k\left( {A - \Delta {l_0}} \right)\) (lúc vật ở vị trí cao nhất)

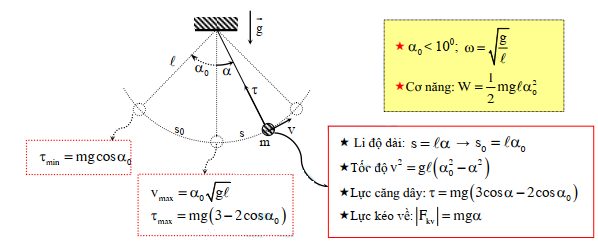
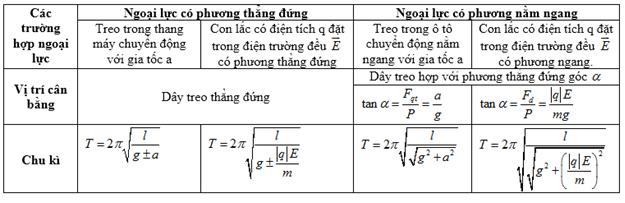
III. Con lắc đơn

 

Con lắc đơn chịu tác dụng của ngoại lực:

 

IV. Dao động tắt dần, dao động cưỡng bức

- Khi không có ma sát, con lắc dao động điều hòa với tần số riêng \({f_0}\) chỉ phụ thuộc vào các đặc tính của con lắc.

- Dao động có biên độ giảm dần theo thời gian gọi là dao động tắt dần. Nguyên nhân làm tắt dần dao động là do lực ma sát và lực cản của môi trường.

- Dao động được duy trì bằng cách giữ cho biên độ không đổi mà không làm thay đổi chu kì dao động riêng gọi Là dao động duy trì. (ví dụ: dao động của đồng hồ quả lắc).

- Dao động chịu tác dụng của một ngoại lực cưỡng bức tuần hoàn gọi là dao động cưỡng bức. Dao động cưỡng bức có  biên độ không đổi và có tần số bằng tần số f của lực cưỡng bức.

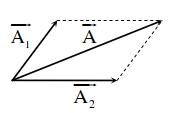
V. Tổng hợp dao động điều hòa

 

+ Biên độ dao động tổng hợp: \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\left( {{\varphi _2} - {\varphi _1}} \right)\)

Điều kiện biên độ: \(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)

+ Pha: \(\tan \varphi {\rm{\;}} = \frac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}{\rm{cos}}{\varphi _1} + {A_2}{\rm{cos}}{\varphi _2}}}\) \(\left( {{\varphi _1} \le \varphi {\rm{\;}} \le {\varphi _2}} \right)\)

---

Chương 2

CHƯƠNG 2: SÓNG CƠ VÀ SÓNG ÂM

I. Sóng cơ và sự truyền sóng cơ

1. Định nghĩa:

- Sóng cơ là dao động cơ lan truyền trong môi trường vật chất.

- Sóng ngang là sóng trong đó các phần rử môi trường dao động theo phương vuông góc với phương truyền sóng. (trừ trường hợp sóng mặt nước, sóng ngang chỉ truyền đuợc trong chất rắn).

- Sóng dọc là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng. Sóng dọc  truyền được cả trong chất khí, chất lỏng và chất rắn.

- Khi có sóng, các phần tử môi trường chỉ dao động tại chỗ, pha của dao động được truyền đi.

- Các phần tử môi trường nơi có sóng truyền qua đều dao động cùng chu kì, tần số với nguồn phát dao động. Khi truyền từ môi trườg này sang môi trường khác chỉ có tần số không thay đổi.

- Tốc độ truyền sóng: là tốc độ lan truyền dao động, nó phụ thuộc vào bản chất môi trường (tính đàn hồi và mật độ vật chất môi trường). Đối với mỗi môi trường tốc độ có giá trị xác định.

- Bước sóng: là khoảng cách giữa hai phần tử sóng gần nhau nhất trên phương truyền sóng dao động cùng pha. Bước sóng cũng là quãng đường mà sóng truyền đi được trong một chu kì.

\(\lambda  = vT = \frac{v}{f}\)

2. Phương trình sóng

Phương trình tại nguồn: \({u_0} = Ac{\rm{os}}\omega {\rm{t}}\)

Phương trình sóng tại một điểm M trên phương truyền sóng Ox là: \(u = Acos\left( {\omega t + \varphi {\rm{\;}} \pm \frac{{2\pi d}}{\lambda }} \right)\)

+ Nếu M ở trước O theo chiều truyền sóng thì \({\varphi _M} = \varphi {\rm{\;}} + {\rm{ }}2\pi \frac{x}{\lambda }\)

+ Nếu M ở sau O theo chiều truyền sóng thì \({\varphi _M} = \varphi {\rm{\;}} - 2\pi \frac{x}{\lambda }\)

3. Độ lệch pha

Độ lệch pha \(\Delta \varphi {\rm{\;}} = \frac{{2\pi d}}{\lambda }\) , trong đó \(d\)- khoảng cách hai điểm

+ Hai điểm dao động cùng pha nếu: \(\Delta \varphi {\rm{\;}} = k2\pi \)  hay \(d = k\lambda \)

+ Hai điểm dao động ngược pha nếu: \(\Delta \varphi {\rm{\;}} = \left( {2k + 1} \right)\pi \) hay \(d = \left( {2k + 1} \right)\frac{\lambda }{2}\)

+ Hai điểm dao động vuông pha nếu: \(\Delta \varphi {\rm{\;}} = \left( {2k + 1} \right)\frac{\pi }{2}\) hay \(d = \left( {2k + 1} \right)\frac{\lambda }{4}\)

II. Giao thoa sóng

- Hai nguồn kết hợp là hai nguồn dao động cùng phương, cùng chu kì (hay tần số) và có hiệu số pha không thay đổi theo thời gian. Hai nguồn kết hợp có cùng pha là hai nguồn đồng bộ.

- Hai sóng do hai nguồn kết hợp phát ra là hai sóng kết hợp.

- Hiện tượng giao thoa là hiện tượng hai sóng kết hợp khi gặp nhau thì có những điểm ở đó chúng luôn luôn tăng cường lẫn nhau, có những điểm ở đó chúng luôn luôn triệt tiêu nhau.

Xét với hai nguồn cùng pha, ta có:

+ Biên độ dao động tổng hợp tại M: \({A_M} = \left| {2acos\left( {\frac{{\pi \left( {{d_1} - {d_2}} \right)}}{\lambda }} \right)} \right|\)

+ Điểm có biên độ cực đại khi: \(\Delta d = {d_1} - {d_2} = k\lambda \)

+ Điểm có biên độ cực tiểu khi: \(\Delta d = {d_1} - {d_2} = \left( {2k + 1} \right)\frac{\lambda }{2}\)

+ Số điểm dao động cực đại, cực tiểu giữa hai nguồn AB (không tính hai nguồn)

* Số Cực đại: \( - \frac{l}{\lambda }{\rm{\;}} < k < {\rm{\;}} + \frac{l}{\lambda }\)

* Số Cực tiểu: \( - \frac{l}{\lambda } - \frac{1}{2} < k < {\rm{\;}} + \frac{l}{\lambda } - \frac{1}{2}{\rm{\;\;\;\;}}({\rm{k}} \in {\rm{Z}})\)Hay  \( - \frac{l}{\lambda } < k + 0,5 < {\rm{\;}} + \frac{l}{\lambda }{\rm{\;\;\;\;}}({\rm{k}} \in {\rm{Z}})\)

III. Sóng dừng

1. Định nghĩa

Sóng dừng là kết quả giao thoa của sóng tới và sóng phản xạ. Sóng tới và sóng phản xạ nếu truyền theo cùng một phương, thì có thể giao thoa với nhau, và tạo ra một hệ sóng dừng.

Trong sóng dừng có một số điểm luôn luôn đứng yên gọi là nút, và một số điểm luôn luôn dao động với biên độ cực đại gọi là bụng.

+ Khoảng cách giữa 2 nút hoặc 2 bụng liền kề của sóng dừng là \(\frac{\lambda }{2}\).

+ Khoảng cách giữa nút và bụng liền kề là \(\frac{\lambda }{4}\) .

+ Khoảng cách giữa hai nút (bụng, múi) sóng bất kỳ là : \(k\frac{\lambda }{2}\)

2. Điều kiện để có sóng dừng

a) Hai đầu cố định

\(l = k\frac{\lambda }{2}\left( {k \in N*} \right)\)

- Số bụng sóng = số bó sóng = k

- Số nút sóng = k + 1

b) Một đầu cố định một đầu tự do

\(l = \left( {2k + 1} \right)\frac{\lambda }{4}\left( {k \in N*} \right)\)

- Số bó (bụng) sóng nguyên = k

- Số bụng sóng = số nút sóng = k+1

IV. Sóng âm

- Các đặc trưng vật lí của âm:

+ Tần số \(f\)

+ Cường độ âm: \(I = \frac{{\rm{W}}}{{St}} = \frac{P}{S} = \frac{P}{{4\pi {r^2}}}\)

+ Mức cường độ âm: \(L = \log \frac{I}{{{I_0}}}\left( B \right) = 10\log \frac{I}{{{I_0}}}\left( {dB} \right)\)

- Các đặc trưng sinh lí của âm

+ Độ cao: là một đặc trưng sinh lí phụ thuộc vào tần số âm, không phụ thuộc vào năng lượng âm.

+ Độ to: là 1 đặc trưng sinh lí phụ thuộc vào tần số âm và mức cường độ âm.

+ Âm sắc: là đặc trưng của âm giúp ta phân biệt được các âm phát ra từ các nguồn khác nhau. Âm sắc liên quan đến đồ thị dao động âm.

---

Chương 3

CHƯƠNG 3: DÒNG ĐIỆN XOAY CHIỀU

I. Đại cương về dòng điện xoay chiều

1. Định nghĩa

- Dòng điện xoay chiều được hiểu là dòng điện có cường độ là hàm số sin hay cosin của thời gian: \(i = {I_0}\cos \left( {\omega t + \varphi } \right)\)

Trong đó:

i: cường độ dòng điện tức thời

I₀: cường độ dòng điện cực đại (I₀ > 0)

\(\omega \): tần số góc (rad/s)

\(\left( {\omega t + \varphi } \right)\): pha của dòng điệnn tại thời điểm t

- Chu kì: \(T = \frac{{2\pi }}{\omega }\) (s); tần số \(f = \frac{\omega }{{2\pi }} = \frac{1}{T}\) (Hz)

- Điện lượng qua tiết diện S trong thời gian t: q = i.t

- Điện lượng qua tiết diện S trong thời gian t₁ đến t₂: \(\Delta q = \int\limits_{{t_1}}^{{t_2}} {i{\rm{d}}t} \)

2. Chú ý

- Khi tính toán, đo lường,… các đại lượng của mạch điện xoay chiều, người ta chủ yếu tính hoặc đo các giá trị hiệu dụng: \(I = \frac{{{I_0}}}{{\sqrt 2 }};U = \frac{{{U_0}}}{{\sqrt 2 }}\)

- Trong một chu kì, dòng điện đổi chiều 2 lần.

- Người ta tạo ra dòng điện xoay chiều bằng máy phát điện xoay chiều, máy này hoạt động dựa trên hiện tượng cảm ứng điện từ.

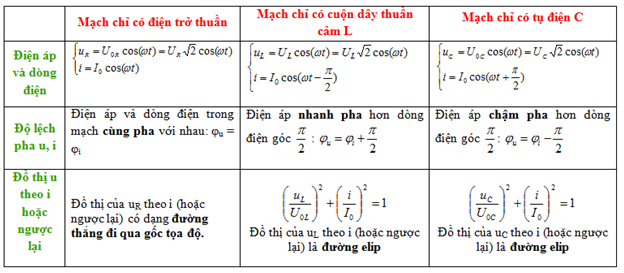
II. Các mạch điện xoay chiều

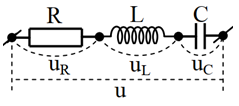
III. Mạch RLC

 

- Biểu thức điện áp: \(u = {u_R} + {u_L} + {u_C} = {U_0}\cos \left( {\omega t + {\varphi _u}} \right)\)

- Biểu thức dòng điện: \(i = {I_0}\cos \left( {\omega t + {\varphi _i}} \right)\)

- Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)

- Cường độ dòng điện cực đại: \({I_0} = \frac{{{U_0}}}{Z} = \frac{{{U_{0{\rm{R}}}}}}{R} = \frac{{{U_{0L}}}}{{{Z_L}}} = \frac{{{U_{0C}}}}{{{Z_C}}}\)

- Độ lệch pha của u so với i: \(\tan \varphi  = \frac{{{Z_L} - {Z_C}}}{R} = \frac{{{U_L} - {U_C}}}{{{U_R}}}\)

- Công suất: \(P = UIcos\varphi {\rm{\;}} = {I^2}R = \frac{{{U^2}R}}{{{Z^2}}} = \frac{{{U^2}R}}{{{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}}}\)

- Hệ số công suất: \(\cos \varphi  = \frac{{{U_{0{\rm{R}}}}}}{{{U_0}}} = \frac{R}{Z}\)

- Cộng hưởng điện xảy ra khi \({Z_L} = {Z_C}\) hay \({\omega ^2}LC = 1\). Khi đó:

+ Tổng trở nhỏ nhất \({Z_{\min }} = R\)

+ Dòng điện lớn nhất: \({I_{\max }} = \frac{U}{R}\)

+ \(\varphi  = 0\): u và i cùng pha (u trễ pha \(\frac{\pi }{2}\) so với u_L; u sớm pha \(\frac{\pi }{2}\) so với u_C )

+ Hệ số công suất cực đại: \(P = \frac{{{U^2}}}{R} = UI\)

+ \({U_{R\max }} = U;{U_L} = {U_C}\)