Câu 25 trang 112 SGK Hình học 11 Nâng cao
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
Đề bài
Cho hai mặt phẳng vuông góc (P) và (Q) có giao tuyến Δ. Lấy A, B cùng thuộc Δ và lấy C ϵ (P), D ϵ (Q) sao cho AC ⊥ AB, BD ⊥ AB và AB = AC = BD. Xác định thiết diện của tứ diện ABCD khi cắt bởi mặt phẳng (α) đi qua điểm A và vuông góc với CD. Tính diện tích thiết diện khi AC = AB = BD = a.
Lời giải chi tiết
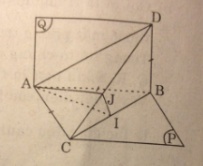
Gọi I là trung điểm của BC thì AI ⊥ BC. Do BD ⊥ mp(ABC) nên AI ⊥ CD (định lí ba đường vuông góc).
Trong mp(CDB), kẻ IJ vuông góc với CD (J ϵ CD) thì mp(AIJ) chính là mặt phẳng (α) và thiết diện phải tìm là tam giác AIJ
Tam giác AIJ là tam giác vuông tại I.
Mẹo Tìm đáp án nhanh nhất
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 25 trang 112 SGK Hình học 11 Nâng cao timdapan.com"
Search google: "từ khóa + timdapan.com" Ví dụ: "Câu 25 trang 112 SGK Hình học 11 Nâng cao timdapan.com"







