Bài tập cuối tuần Toán 5 tuần 29 - Đề 2 (Có đáp án và lời giải chi tiết)

Đề bài

Bài 1. a) Đọc các số sau:

30 815;          175 860;         5 239 070;         722 360 593.

b) Nêu giá trị của chữ số 5 trong mỗi số trên. 

………………………………………………………………………………………………

………………………………………………………………………………………………

………………………………………………………………………………………………

Bài 2. So sánh các phân số:

a) \(\dfrac{2}{5}\) và \(\dfrac{3}{4}\)                     b) \(\dfrac{{15}}{{28}}\) và \(\dfrac{2}{7}\)                     c) \(\dfrac{8}{7}\) và \(\dfrac{7}{8}\)

………………………………………………………………………………………………

………………………………………………………………………………………………

………………………………………………………………………………………………

Bài 3. Viết các số sau theo thứ tự từ bé đến lớn: 

a) 4,5 ;  2,54 ;   5, 24 ;   5,42.

b) 71,2 ;   68,9 ;    68,888 ;   80 ;    72,1.

………………………………………………………………………………………………

………………………………………………………………………………………………

………………………………………………………………………………………………

Bài 4. Viết số thích hợp vào chỗ chấm (theo mẫu):

a) 2535m = 2km 535m = 2,535km.

    8267m = ... km ... m = ... , … km

    6034m = ... km ... m = ... , …  km

    401m = ... km... m = ... , …  km.

b) 48dm = .. m ... dm = ... , …  m

    678cm = ... m ... cm = ... , …  m

    905cm = ... m ... cm = ... , …  m

c) 2568g = 2kg 568g = 2,568kg

    2085g = ... kg ... g = ... , …  kg

    4042kg = ... tấn ... kg = ... , …  tấn.

Bài 5. Viết các số đo khối lượng dưới dạng số thập phân :

a) 5 tấn 762kg = …. tấn ;                  

b) 3 tấn 65kg   = …… tấn ;

c) 1985kg =….. tấn ;

d) 89kg = ….  tấn ;

e) 4955g =…. kg ;  

 g) 285g = ……kg.

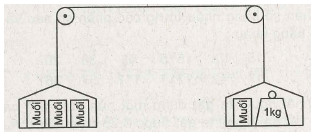
Bài 6. Mỗi gói muối đều cân nặng như nhau và cân đã thăng bằng. Hỏi mỗi gói muối cân nặng bao nhiêu gam?

………………………………………………………………………………………………

………………………………………………………………………………………………

………………………………………………………………………………………………

Lời giải chi tiết

Bài 1.

a) Để đọc các số ta đọc từ trái sang phải, hay từ hàng cao đến hàng thấp.

b) Xác định vị trí của chữ số 5 trong mỗi số đó rồi ghi giá trị tương ứng của chữ số đó.  

Cách giải:

a) Số 30 815 đọc là: ba mươi nghìn tám trăm mười lăm.

Số 175 860 đọc là: một trăm bảy mươi lăm nghìn tám trăm sáu mươi.

Số 5 239 070 đọc là: năm triệu hai trăm ba mươi chín nghìn không trăm bảy mươi.

Số 722 360 593 đọc là: bảy trăm hai mươi hai triệu ba trăm sáu mươi nghìn năm trăm chín mươi ba

b) Chữ số 5 trong số 30 815 thuộc hàng đơn vị nên có giá trị là 5.

Chữ số 5 trong số 175 860 thuộc hàng nghìn nên có giá trị là 5000.

Chữ số 5 trong số 5 239 070 thuộc hàng triệu nên có giá trị là 5 000 000.

Chữ số 5 trong số 722 360 593 thuộc hàng trăm nên có giá trị là 500. 

Bài 2.

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số rồi so sánh hai phân số sau khi quy đồng.

Cách giải:

a) \(\dfrac{2}{5}\) và \(\dfrac{3}{4}\)

Ta có: \(\dfrac{2}{5} = \dfrac{{2 \times 4}}{{5 \times 4}} = \dfrac{8}{{20}}\,\,;\)                \(\dfrac{3}{4} = \dfrac{{3 \times 5}}{{4 \times 5}} = \dfrac{{15}}{{20}}.\)

Mà: \(\dfrac{8}{{20}} < \dfrac{{15}}{{20}}\)(vì 8 < 15).

Vậy: \(\dfrac{2}{5} < \dfrac{3}{4}.\)

b) \(\dfrac{{15}}{{28}}\) và \(\dfrac{2}{7}\)

Ta có:          \(\dfrac{2}{7} = \dfrac{{2 \times 4}}{{7 \times 4}} = \dfrac{8}{{28}}\,\,;\)                Giữ nguyên phân số \(\dfrac{{15}}{{28}}.\)

Mà: \(\dfrac{{15}}{{28}} > \dfrac{8}{{28}}\)(vì 15 > 8).

Vậy: \(\dfrac{{15}}{{28}} > \dfrac{2}{7}.\)

c) \(\dfrac{8}{7}\) và \(\dfrac{7}{8}\)

Ta có: \(\dfrac{8}{7} = \dfrac{{8 \times 8}}{{7 \times 8}} = \dfrac{{64}}{{56}}\,\,;\)           \(\dfrac{7}{8} = \dfrac{{7 \times 7}}{{8 \times 7}} = \dfrac{{49}}{{56}}.\)

Mà: \(\dfrac{{64}}{{56}} > \dfrac{{49}}{{56}}\)(vì 64 > 49).

Vậy: \(\dfrac{8}{7} > \dfrac{7}{8}.\)

Cách khác:

Ta có:  \(\dfrac{8}{7} > 1\) (vì 8 > 7) và \(\dfrac{7}{8} < 1\)(vì 7 < 8).

Hay: \(\dfrac{8}{7} > 1 > \dfrac{7}{8}.\)

Vậy: \(\dfrac{8}{7} > \dfrac{7}{8}.\)

Bài 3.

Phương pháp:

So sánh các số thập phân, sau đó sắp xếp các số thập phân theo thứ tự từ bé đến lớn.

Cách giải:

a) So sánh các số thập phân ta có:

2,54  <  4,5  <  5,24  <  5,42.

Vậy các số được viết theo thứ tự từ bé đến lớn là:

2,54 ;  4,5 ;  5,24 ;  5,42.

a) So sánh các số thập phân ta có:

68,888 < 68,9 < 71,2 < 72,1 < 80.

Vậy các số được viết theo thứ tự từ bé đến lớn là:

68,888 ;  68,9 ;  71,2 ;  72,1 ;  80.

Bài 4.

Phương pháp:

- Quan sát ví dụ mẫu rồi làm tương tự với các câu còn lại.

- Áp dụng kiến thức:

1 tấn = 1000kg, hay 1kg = \(\dfrac{1}{{1000}}\) tấn = 0,001 tấn ;

1kg = 1000g, hay 1g = \(\dfrac{1}{{1000}}\)kg = 0,001kg.

Cách giải:

a) 2535m = 2km 535m = 2,535km

    8267m = 8km 267m = 8,267km

    6034m = 6km 34m = 6,034km

    401m = 0 km 401m = 0,401km

b) 48dm = 4m 8dm = 4,8m

    678cm = 6m 78cm = 6,78m

    905cm = 9m 5cm = 9,05m

c) 2568g = 2kg 568g = 2,568kg

    2085g = 2 kg 85g = 2,085kg

    4042kg = 4 tấn 42kg = 4,042 tấn.

Bài 5.

Phương pháp:

Áp dụng kiến thức:

1 tấn = 1000kg, hay 1kg = \(\dfrac{1}{{1000}}\) tấn = 0,001 tấn ;

1kg = 1000g, hay 1g = \(\dfrac{1}{{1000}}\)kg = 0,001kg.

Cách giải:

a) 5 tấn 762kg = 5,762 tấn         

b) 3 tấn 65kg  = 3,065 tấn         

c) 1985kg = 1,985 tấn                              

d) 89kg = 0,089 tấn

e) 4955g = 4,955kg                         

g) 285g = 0,285kg.

Bài 6.

Phương pháp:

Theo hình vẽ ta thấy 2 gói muối cân nặng 1kg hay 1000g, từ đó ta tìm được cân nặng của mỗi gói  muối.

Cách giải:

Theo hình vẽ ta thấy 2 gói muối cân nặng 1kg hay 1000g.

Mỗi gói muối cân nặng số gam là:

             1000 : 2 = 500 (g)

                           Đáp số: 500g.