Bài 9 trang 39 SGK Toán 9 tập 2
Giải bài 9 trang 39 SGK Toán 9 tập 2. Cho hai hàm số
Đề bài
Cho hai hàm số \(y = \dfrac{1 }{3}{x^2}\) và \(y = -x + 6\).
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ các giao điểm của hai đồ thị đó.
Phương pháp giải - Xem chi tiết
a) Cách vẽ đồ thị hàm số \(y=ax^2\):
Bước 1: Xác định 2 điểm thuộc đồ thị và các điểm đối xứng của chúng qua \(Oy\).
Bước 2: Vẽ parabol đi qua gốc \(O(0;0)\) và các điểm trên.
+) Cách vẽ đồ thị hàm số \(y=ax+b\):
Cho \(x=0 \Rightarrow y=b\). Đồ thị hàm số đi qua điểm \(A(0; b)\).
Cho \(y=0 \Rightarrow x =\dfrac{-b}{a}\). Đồ thị hàm số đi qua điểm \(B{\left(\dfrac{-b}{a}; 0 \right)}\)
Đồ thị hàm số là đường thẳng đi qua hai điểm \(A\) và \(B\).
b) Tìm tọa độ giao điểm của hai đồ thị hàm số \(y=ax+b\) và \(y=a'x^2\). Ta xét phương trình hoành độ giao điểm: \(ax+b=a'x^2\). Giải phương trình này tìm được hoành độ giao điểm. Thay giá trị đó vào công thức hàm số tìm được tung độ giao điểm.
Lời giải chi tiết
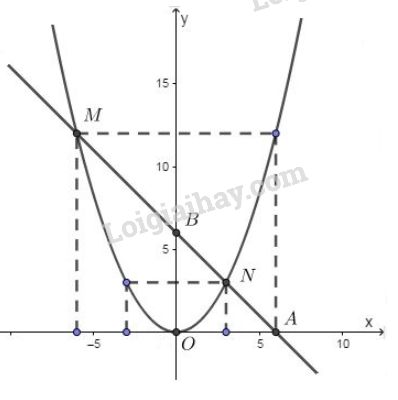
a) *Vẽ đồ thị: \(y = \dfrac{1 }{3}{x^2}\).
Bảng giá trị:
|
\(x\) |
\(-6\) |
\(-3\) |
\(0\) |
\(3\) |
\(6\) |
|
\(y=\dfrac{1}{3}x^2\) |
\(12\) |
\(3\) |
\(0\) |
\(3\) |
\(12\) |
Vẽ parabol đi qua gốc tọa độ và các điểm có tọa độ \(\left( { - 6;12} \right),\left( { - 3;3} \right),\left( {3;3} \right),\left( {6;12} \right)\) ta được đồ thị hàm số \(y = \dfrac{1 }{3}{x^2}\).
*Vẽ đồ thị: \(y = -x + 6\)
- Cho \(x = 0 \Rightarrow y = 0+6=6\). Đồ thị đi qua \(B(0; 6)\).
- Cho \(y = 0 \Rightarrow 0= -x+6 \Rightarrow x=6\). Đồ thị hàm số đi qua \(A(6; 0)\).
Đồ thị hàm số \(y=-x+6\) là đường thẳng đi qua hai điểm \(A,B\).
Vẽ đồ thị: xem hình bên dưới.
b) Xét phương trình hoành độ giao điểm:
\(\dfrac{1}{3}x^2=-x+6\)
\(\Leftrightarrow \dfrac{1}{3}x^2 +x -6=0\)
\(\Leftrightarrow x^2+3x-18=0\)
\(\begin{array}{l}\Leftrightarrow{x^2} - 3x + 6x - 18 = 0\\ \Leftrightarrow x\left( {x - 3} \right) + 6\left( {x - 3} \right) = 0\\ \Leftrightarrow \left( {x + 6} \right)\left( {x - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 6 = 0\\x - 3 = 0\end{array} \right.\end{array}\)
\( \Leftrightarrow \left[ \matrix{
x = -6 \hfill \cr
x = 3 \hfill \cr} \right.\)
Với \(x=3 \Rightarrow y=-3+6=3\). Đồ thị hàm số đi qua điểm \(N(3;3)\).
Với \(x=-6 \Rightarrow y=-(-6)+6=12\). Đồ thị hàm số đi qua điểm \(M(-6;12)\).
Vậy giao điểm của hai đồ thị là \(N(3;3)\) và \(M(-6;12)\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 9 trang 39 SGK Toán 9 tập 2 timdapan.com"