Bài 7 trang 15 SGK Hình học 12 Nâng cao

Tìm các mặt phẳng đối xứng của các hình sau đây :

LG a

Hình chóp tứ giác đều ;

Lời giải chi tiết:

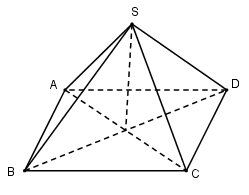
Các mặt phẳng đối xứng của hình chóp tứ giác đều \(S.ABCD\) là các mặt phẳng:

- Mp\((SAC)\)

- Mp\((SBD)\)

- Mặt phẳng trung trực của đoạn \(AB\).

- Mặt phẳng trung trực của đoạn \(AD\).

Chú ý:

Chứng minh cụ thể như sau:

Xét hình chóp tứ giác đều S.ABCD

- Dễ thấy (SAC) là mặt phẳng trung trực của BD nên phép đối xứng qua (SAC) biến các đỉnh S, A, B, C, D lần lượt thành các đỉnh S, A, D, C, B hay biến hình chóp S.ABCD thành chính nó. Vậy (SAC) là một mặt phẳng đối xứng của hình chóp S.ABCD.

Tương tự (SBD) cũng là một mp đối xứng của hình chóp S.ABCD .

- Lại có, mặt phẳng trung trực của cạnh AB đồng thời là mặt phẳng trung trực của cạnh CD và chứa S nên đó là một mặt đối xứng của hình chóp S.ABCD. tương tự mặt phẳng trung trực của AD cũng là một mặt phẳng đối xứng của hình chóp S.ABCD.

- Kết luận: Hình chóp tứ giác đều S.ABCD có 4 mặt phẳng đối xứng là (SAC), (SBD) , mặt phẳng trung trực của cạnh AD và AD.

LG b

Hình chóp cụt tam giác đều ;

Lời giải chi tiết:

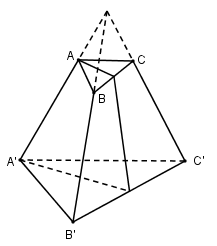
Hình chóp cụt tam giác đều \(ABC.A’B’C’\) có ba mặt phẳng đối xứng, đó là ba mặt phẳng trung trực của ba cạnh \(AB, BC, CA\).

Chứng minh:

Xét hình chóp cụt tam giác đều ABC.A’B’C’

Gọi S là điểm đồng quy của AA’, BB’, CC’, M, N, P lần lượt là trung điểm của BC, CA, AB.

Ta có (SAM) là mặt phẳng trung trực của BC, cũng là mặt phẳng trung trực của B’C’.

Mặt khác, A’ ∈ SA => A’ ∈ mp (SAM). Vậy phép đôi xứng qua mp(SAM) biến các đỉnh A, B, C, A’, B’, C’ lần lượt thành A, C; B, A’, C’, B’ do đó biến hình chóp cụt tam giác đều ABC.A’B’C’ thành chính nó hay (SAM) là một mp đối xứng là (SAM), (SBN), (SCP).

Tương tự các mặt phẳng là (SBN), (SCP) cũng là mặt phẳng đối xứng.

LG c

Hình hộp chữ nhật mà không có mặt nào là hình vuông.

Lời giải chi tiết:

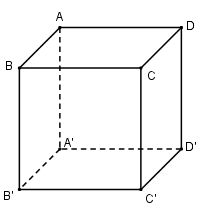Hình hộp chữ nhật \(ABCD.A’B’C’D’\) (mà không có mặt nào là hình vuông) có ba mặt phẳng đối xứng, đó là ba mặt phẳng trung trực của ba cạnh \(AB, AD, AA’\).

Chứng minh:

Xét hình hộp chữ nhật ABCD.A’B’C’D’ mà không có mặt nào là hình vuông.

- Gọi (P) là mặt phẳng trung trực của cạnh AB thì (P) cũng là mặt phẳng trung trực của các cạnh CD, D’C’, A’B’ nếu cho phép đối xứng qua (P) biến A, B, C, D, A’, B’, C’, D’ lần lượt thành B, A, D, C, B’, A’, D’, C’ hay phép đối xứng qua (P) biến hình hộp của hình chữ nhật ABCD.A’B’C’D’ thành chính nó. Vậy (P) là một mặt phẳng đối xứng của hình hộp chữ nhật.

Tương tự, mặt phẳng trung trực của các cạnh AA’, AD cũng là các mặt phẳng đối xứng của hình hộp chữ nhật ABCD.A’B’C’D’.

Kết luận: hình hộp chữ nhật mà không có mặt phẳng nào là hình vuông có 3 mặt phẳng đối xứng là 3 mặt phẳng trung trực của 3 cạnh cùng xuất phát tại một đỉnh.