Bài 69 trang 141 SGK Toán 7 tập 1

Đề bài

Cho điểm \(A\) nằm ngoài đường thẳng \(a.\) Vẽ cung tròn tâm \(A\) cắt đường thẳng \(a\) ở \(B\) và \(C.\) Vẽ các cung tròn tâm \(B\) và tâm \(C\) có cùng bán kính sao cho chúng cắt nhau tại một điểm khác \(A\), gọi điểm đó là \(D\). Hãy giải thích vì sao \(AD\) vuông góc với đường thẳng \(a.\)

Lời giải chi tiết

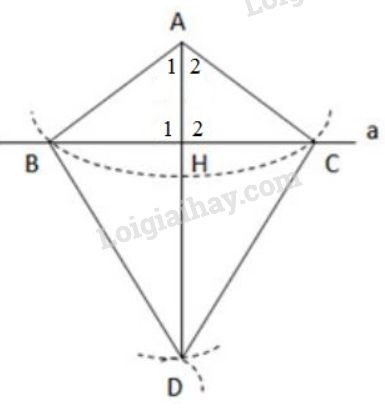
Xét \(∆ABD\) và \(∆ACD\) có:

\(AB = AC\) (bằng bán kính cung tròn tâm \(A\))

\(DB = DC\) (vì cung tròn tâm \(B\) và tâm \(C\) có cùng bán kính)

\(AD\) cạnh chung

\( \Rightarrow ∆ABD = ∆ACD\) (c.c.c)

\( \Rightarrow\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)

Gọi \(H\) là giao điểm của \(AD\) và \(a.\)

Xét \(∆AHB\) và \(∆AHC\) có:

\(AB = AC\) (bằng bán kính cung tròn tâm \(A\))

\(\widehat {{A_1}} = \widehat {{A_2}}\) (chứng minh trên)

\(AH\) cạnh chung

\( \Rightarrow  ∆AHB = ∆AHC\) (c.g.c)

\( \Rightarrow \widehat {{H_1}} = \widehat {{H_2}}\) (hai góc tương ứng)

Ta lại có: \(\widehat {{H_1}} + \widehat {{H_2}} = {180^o}\) (hai góc kề bù)

\( \Rightarrow \widehat {{H_1}} = \widehat {{H_2}} = {90^o}\)

Vậy \(AD ⊥ a\) (điều phải chứng minh).